弧长和扇形的面积
图片预览

文档简介
周期律 28.3.1弧长和扇形的面积
教学内容
28.1弧长和扇形的面积
课型
新授课
主备人
执教人
教学目标
1、了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用.
2、通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长L=和扇形面积S扇=的计算公式,并应用这些公式解决一些题目.
教学重点
n°的圆心角所对的弧长L=,扇形面积S扇=及其它们的应用
问题引入:
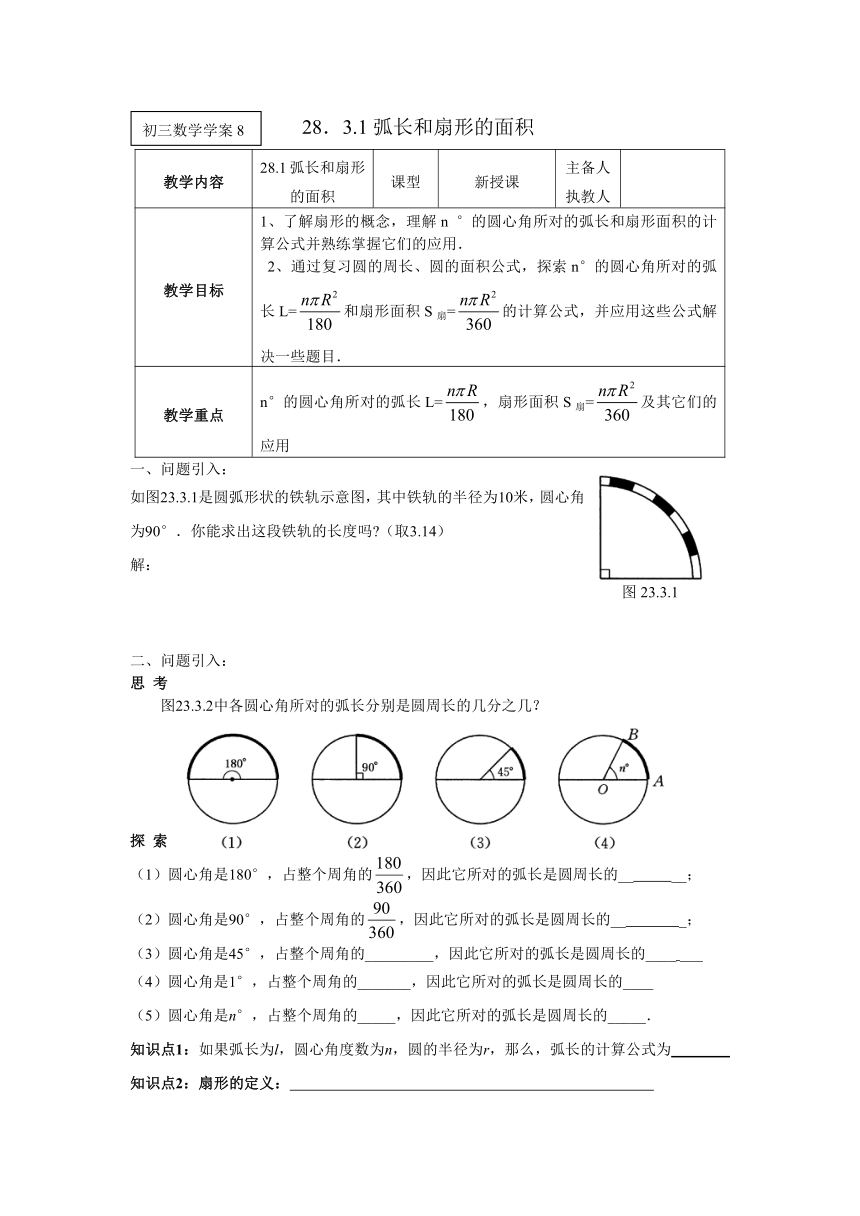
如图23.3.1是圆弧形状的铁轨示意图,其中铁轨的半径为10米,圆心角为90°.你能求出这段铁轨的长度吗?(取3.14)
解:
问题引入:
思 考
图23.3.2中各圆心角所对的弧长分别是圆周长的几分之几?
探 索
(1)圆心角是180°,占整个周角的,因此它所对的弧长是圆周长的__ __;
(2)圆心角是90°,占整个周角的,因此它所对的弧长是圆周长的__ _;
(3)圆心角是45°,占整个周角的_________,因此它所对的弧长是圆周长的____ ___
(4)圆心角是1°,占整个周角的_______,因此它所对的弧长是圆周长的____
(5)圆心角是n°,占整个周角的_____,因此它所对的弧长是圆周长的_____.
知识点1:如果弧长为l,圆心角度数为n,圆的半径为r,那么,弧长的计算公式为
知识点2:扇形的定义:
思 考
圆心角为1°的扇形面积以及圆心角为n°的扇形面积分别是圆面积的几分之几?
探 索
(1) 如图,圆心角是180°,占整个周角的,因此圆心角是180°的扇形面积是圆面积的_________;
(2) 圆心角是90°,占整个周角的____ ____,因此圆心角是90°的扇形面积是圆面积的_____ ___;
(3) 圆心角是45°,占整个周角的________,因此圆心角是45°的扇形面积是圆面积的____ ____;
(4) 圆心角是1°,占整个周角的________,因此圆心角是1°的扇形面积是圆面积的_____ ____;
(5) 圆心角是n°,占整个周角的________,因此圆心角是n°的扇形面积是圆面积的______ ___.
如果设圆心角是n°的扇形面积为S,圆的半径为r,那么扇形的面积为
.
因此扇形面积的计算公式为
或 .
如图23.3.5,圆心角为60°的扇形的半径为10厘米,求这个扇形的面积和周长.(π≈3.14)
练 习
填空题:
(1)如果扇形的圆心角是230°,那么这个扇形的面积等于这个扇形所在圆的面积的_______________;
(2) (2012内蒙古)已知扇形的面积为12,半径是6,则它的圆心角是 。
(3)扇形的面积是S,它的半径是r,这个扇形的弧长是_____________.
2、(2012内蒙古巴彦淖尔、赤峰)如图,等圆⊙O1 和⊙O2 相交于A,B两点,⊙O2 经过⊙O1 的圆心O1,两圆的连心线交⊙O1于点M,交AB于点N,连接BM,已知AB=2。
求证:BM是⊙O2的切线;
(2)求 的长。
三、课后作业:
1、填空题
(1)已知圆心角为150°,所对的弧长为20π,则圆的半径为 ;
(2)已知半径为3,则弧长为π的弧所对的圆心角为
(3)在⊙O中,如果120°的圆心角所对应的弧长为π,则⊙O的半径为
2、选择题
(1)如果圆的半径为6,那么600的圆心角所对的弧长为 ( )
A、π B、2π C、3π D、6π
(2)已知扇形的圆心角为120°,半径为3cm,那么扇形的面积为( )
★3、解答题:
如图,在一个横截面为Rt△ABC的物体中,∠ACB=∠CAB=30°,BC=1米。工人师傅把此物体搬到墙边,先将AB边放在地面(直线)上,再按顺时针方向绕点B翻转到△的位置(在上),最后沿的方向平移到△的位置,其平移的距离为线段AC的长度(此时恰好靠在墙边)。
请直接写出AB、AC的长;
画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米)。
教学内容
28.1弧长和扇形的面积
课型
新授课
主备人
执教人
教学目标
1、了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用.
2、通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长L=和扇形面积S扇=的计算公式,并应用这些公式解决一些题目.
教学重点
n°的圆心角所对的弧长L=,扇形面积S扇=及其它们的应用
问题引入:
如图23.3.1是圆弧形状的铁轨示意图,其中铁轨的半径为10米,圆心角为90°.你能求出这段铁轨的长度吗?(取3.14)
解:
问题引入:
思 考
图23.3.2中各圆心角所对的弧长分别是圆周长的几分之几?
探 索
(1)圆心角是180°,占整个周角的,因此它所对的弧长是圆周长的__ __;
(2)圆心角是90°,占整个周角的,因此它所对的弧长是圆周长的__ _;
(3)圆心角是45°,占整个周角的_________,因此它所对的弧长是圆周长的____ ___
(4)圆心角是1°,占整个周角的_______,因此它所对的弧长是圆周长的____
(5)圆心角是n°,占整个周角的_____,因此它所对的弧长是圆周长的_____.
知识点1:如果弧长为l,圆心角度数为n,圆的半径为r,那么,弧长的计算公式为
知识点2:扇形的定义:
思 考
圆心角为1°的扇形面积以及圆心角为n°的扇形面积分别是圆面积的几分之几?
探 索
(1) 如图,圆心角是180°,占整个周角的,因此圆心角是180°的扇形面积是圆面积的_________;
(2) 圆心角是90°,占整个周角的____ ____,因此圆心角是90°的扇形面积是圆面积的_____ ___;
(3) 圆心角是45°,占整个周角的________,因此圆心角是45°的扇形面积是圆面积的____ ____;
(4) 圆心角是1°,占整个周角的________,因此圆心角是1°的扇形面积是圆面积的_____ ____;
(5) 圆心角是n°,占整个周角的________,因此圆心角是n°的扇形面积是圆面积的______ ___.
如果设圆心角是n°的扇形面积为S,圆的半径为r,那么扇形的面积为
.
因此扇形面积的计算公式为
或 .
如图23.3.5,圆心角为60°的扇形的半径为10厘米,求这个扇形的面积和周长.(π≈3.14)
练 习
填空题:
(1)如果扇形的圆心角是230°,那么这个扇形的面积等于这个扇形所在圆的面积的_______________;
(2) (2012内蒙古)已知扇形的面积为12,半径是6,则它的圆心角是 。
(3)扇形的面积是S,它的半径是r,这个扇形的弧长是_____________.
2、(2012内蒙古巴彦淖尔、赤峰)如图,等圆⊙O1 和⊙O2 相交于A,B两点,⊙O2 经过⊙O1 的圆心O1,两圆的连心线交⊙O1于点M,交AB于点N,连接BM,已知AB=2。
求证:BM是⊙O2的切线;
(2)求 的长。
三、课后作业:
1、填空题
(1)已知圆心角为150°,所对的弧长为20π,则圆的半径为 ;
(2)已知半径为3,则弧长为π的弧所对的圆心角为
(3)在⊙O中,如果120°的圆心角所对应的弧长为π,则⊙O的半径为
2、选择题
(1)如果圆的半径为6,那么600的圆心角所对的弧长为 ( )
A、π B、2π C、3π D、6π
(2)已知扇形的圆心角为120°,半径为3cm,那么扇形的面积为( )
★3、解答题:
如图,在一个横截面为Rt△ABC的物体中,∠ACB=∠CAB=30°,BC=1米。工人师傅把此物体搬到墙边,先将AB边放在地面(直线)上,再按顺时针方向绕点B翻转到△的位置(在上),最后沿的方向平移到△的位置,其平移的距离为线段AC的长度(此时恰好靠在墙边)。
请直接写出AB、AC的长;
画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米)。
