冀教版七年级数学下册10.1 不等式 课件(共21张PPT)
文档属性
| 名称 | 冀教版七年级数学下册10.1 不等式 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 19:06:08 | ||
图片预览







文档简介
(共21张PPT)
10.1不等式
了解不等式的概念,认识五种不等号的含义.
学会并准确运用不等式表示数量关系.
学会用数学知识解决实际问题,发展应用和自主通过列不等式,训练学生的分析判断能力和逻辑推理能力.
学习目标
1
2
3
了解不等式的概念并准确运用不等式表示数量关系.
学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.
学习重难点
重点:
难点:
情景导入
现实生活中,数量之间存在着相等与不相等的关系.
对于不相等的关系问题,我们如何用式子来表示它们呢?
例如,小明的身高为155cm,小聪的身高为156cm,
则我们可以用不等号“>”或“<”来表示他们的身高之间的关系.
如:156 > 155或155 < 156.
155cm
156cm
探究新知
问题1
小明与小亮进行百米训练,小明先到达终点.小明到达终点所用的时间为15.2 s.如果小亮所用的时间为a s,请回答下列问题:
(1)a 与15.2是同一类量吗?
(2)都是表示什么的量?单位一致吗?
(3)小明先到达终点说明谁用的时间短?
所以有:a 15.2
>
问题2
小明在某一周的零用钱为m元,他在这一周的支出情况如下表:
在略有结余的情况下,请回答下列问题:
(1)m 与60是同一类量吗?
(2)都是表示什么的量?单位一致吗?
(3)“略有结余”说明那个数量大?
所以有:m 60
>
为灾区捐款 就餐 购买文具 买冷饮
5元 50元 3元 2元
探究新知
问题3
在高速公路上,有大、小两辆卡车从甲地向乙地运货。大卡车的行驶速度为60 km/h,小卡车的行驶速度为80 km/h,大卡车比小卡车早出发1h。
(1)如果设小卡车行驶的时间为x h,那么,它行驶的路程该如何表示?这时,大卡车行驶的路程又如何表示?
小卡车行驶路程表示为:80x km
大卡车行驶路程表示为:60(x+1)km
探究新知
(2)小卡车超过大卡车后,它们所行驶的路程之间的关系应怎样表示?
80x>60(x+1)
探究新知
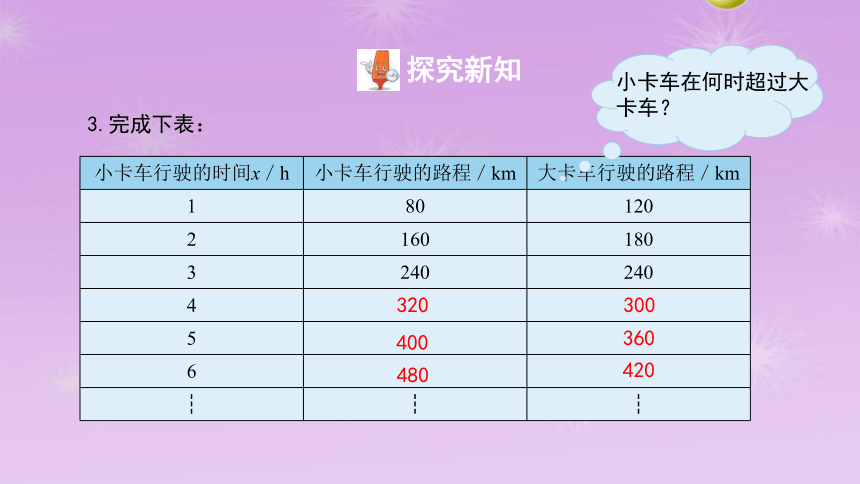
3.完成下表:
小卡车行驶的时间x/h 小卡车行驶的路程/km 大卡车行驶的路程/km
1 80 120
2 160 180
3 240 240
4
5
6
┆ ┆ ┆
320
300
400
360
480
420
探究新知
小卡车在何时超过大卡车?
探究新知
4.小卡车开出多少小时后赶上或超过大卡车?
经探究,我们可以得到小卡车赶上和超过大卡车,两车行驶路程的关系式分别为
由表可知,当
当
即当
想一想
观察式子155 < 156,156 > 155,a > 15.2 , m > 60 , 它们有什么共同点?
所有式子都是用不等号连接而成.
定义:我们把用不等号“>”“<”“≥”或“≤”连接而成的式子叫作不等式.
要点归纳
“≥、≤”的意义:
(1)“≥”:表示“不小于”,读作“大于或等于”;
a不小于(不低于)b表示为______,a为非负数表示为_______;
(2)“≤”:表示“不大于”,读作“小于或等于”.
a不大于(不高过)b表示为______ ,a为非正数表示为_______ .
a≥b
a≥0
a≤b
a≤0
归纳
1.对于含有未知数的不等式,当未知数取某些值时,不等式的左右两边符合不等式所表示的大小关系,我们就说不等式成立;当未知数取某些值时,不等式的左右两边不符合不等式所表示的大小关系,我们就说不等式不成立;
2.使一个含有未知数的不等式成立的数不止一个,是某一范围内的所有数.
练一练
判断下列式子是不是不等式:
(1)-3>0; (2)4x+3y<0;
(3)x=3; (4) x2+xy+y2;
(5)x≠5; (6)x+2>y+5.
解 : (1)(2)(5)(6)是不等式; (3)(4)不是不等式.
做一做
用不等式表示:
(1)y的3倍小于8.
(2)m与10的和不小于m的一半。
(3)汛期,湖水平均每天上涨8cm。现在的水位是340cm,警戒水位是460cm。x天后湖水将超过警戒水位。
解:(1)3y<8.
(2)m+10≥
(3)8x+340>460.
课堂练习
1. 下列各式,不等式一共有______个.
① 5=9-4;
②5>-3;
③x+2≠3+x;
④2+x≥2x-1;
⑤a2+2a+1≤8.
2. 用不等式表示下列数量关系:
(1)a是负数;
(2)x比-3小;
(3)两数m与n的差不大于5.
a < 0;
x <-3;
m-n ≤5.
3
课堂练习
3.在-1,-0.5,0,0.5,1,3,7,100中,哪些能使不等式x+0.5<2成立?
解:当x=-1时,x+0.5=-0.5<右边;
当x=-0.5时,x+0.5=0<右边;
当x=0时,x+0.5=0.5<右边;
当x=0.5时,x+0.5=1<右边;
当x=1时,x+0.5=1.5<右边;
当x=3时,x+0.5=3.5>右边;
当x=7时,x+0.5=7.5>右边;
当x=100时,x+0.5=100.5>右边,所以,当x取-1,-0.5,0,0.5,1时,不等式x+0.5<2成立.
课堂练习
4.(1)雷电的温度大约是28000℃,比太阳表面温度的4.5倍还要高.设太阳表面温度为t℃,那么t应该满足怎样的关系式?
4.5t<28000
(2)黄石市某天的最高气温为+5℃,最低气温比最高气温低8℃,则这天此地气温t(℃)应该满足怎样的关系式?
-3℃≤ t ≤5℃
课堂练习
5.在通过桥洞时,我们往往会看到如图(1)所示的标志,这是限制车高的标志.你知道通过该桥洞的车高x(m)的范围吗?在通过桥面时,我们往往会看到如图(2)所示的标志,这是限制车重的标志.你知道通过该桥面的车重y(t)的范围吗?
(1)
(2)
10t
5m
x≤5m
y≤10t
总结
不等式
列不等式
概念
判断一个式子是否是不等式,主要看这个式子中是否有不等号:
____,____,____,____.
>
<
≥
≤
列不等式的关键是要审清题意,抓住“>”“<”“≥”或“≤”的本质含义.
谢谢听讲!
10.1不等式
了解不等式的概念,认识五种不等号的含义.
学会并准确运用不等式表示数量关系.
学会用数学知识解决实际问题,发展应用和自主通过列不等式,训练学生的分析判断能力和逻辑推理能力.
学习目标
1
2
3
了解不等式的概念并准确运用不等式表示数量关系.
学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.
学习重难点
重点:
难点:
情景导入
现实生活中,数量之间存在着相等与不相等的关系.
对于不相等的关系问题,我们如何用式子来表示它们呢?
例如,小明的身高为155cm,小聪的身高为156cm,
则我们可以用不等号“>”或“<”来表示他们的身高之间的关系.
如:156 > 155或155 < 156.
155cm
156cm
探究新知
问题1
小明与小亮进行百米训练,小明先到达终点.小明到达终点所用的时间为15.2 s.如果小亮所用的时间为a s,请回答下列问题:
(1)a 与15.2是同一类量吗?
(2)都是表示什么的量?单位一致吗?
(3)小明先到达终点说明谁用的时间短?
所以有:a 15.2
>
问题2
小明在某一周的零用钱为m元,他在这一周的支出情况如下表:
在略有结余的情况下,请回答下列问题:
(1)m 与60是同一类量吗?
(2)都是表示什么的量?单位一致吗?
(3)“略有结余”说明那个数量大?
所以有:m 60
>
为灾区捐款 就餐 购买文具 买冷饮
5元 50元 3元 2元
探究新知
问题3
在高速公路上,有大、小两辆卡车从甲地向乙地运货。大卡车的行驶速度为60 km/h,小卡车的行驶速度为80 km/h,大卡车比小卡车早出发1h。
(1)如果设小卡车行驶的时间为x h,那么,它行驶的路程该如何表示?这时,大卡车行驶的路程又如何表示?
小卡车行驶路程表示为:80x km
大卡车行驶路程表示为:60(x+1)km
探究新知
(2)小卡车超过大卡车后,它们所行驶的路程之间的关系应怎样表示?
80x>60(x+1)
探究新知
3.完成下表:
小卡车行驶的时间x/h 小卡车行驶的路程/km 大卡车行驶的路程/km
1 80 120
2 160 180
3 240 240
4
5
6
┆ ┆ ┆
320
300
400
360
480
420
探究新知
小卡车在何时超过大卡车?
探究新知
4.小卡车开出多少小时后赶上或超过大卡车?
经探究,我们可以得到小卡车赶上和超过大卡车,两车行驶路程的关系式分别为
由表可知,当
当
即当
想一想
观察式子155 < 156,156 > 155,a > 15.2 , m > 60 , 它们有什么共同点?
所有式子都是用不等号连接而成.
定义:我们把用不等号“>”“<”“≥”或“≤”连接而成的式子叫作不等式.
要点归纳
“≥、≤”的意义:
(1)“≥”:表示“不小于”,读作“大于或等于”;
a不小于(不低于)b表示为______,a为非负数表示为_______;
(2)“≤”:表示“不大于”,读作“小于或等于”.
a不大于(不高过)b表示为______ ,a为非正数表示为_______ .
a≥b
a≥0
a≤b
a≤0
归纳
1.对于含有未知数的不等式,当未知数取某些值时,不等式的左右两边符合不等式所表示的大小关系,我们就说不等式成立;当未知数取某些值时,不等式的左右两边不符合不等式所表示的大小关系,我们就说不等式不成立;
2.使一个含有未知数的不等式成立的数不止一个,是某一范围内的所有数.
练一练
判断下列式子是不是不等式:
(1)-3>0; (2)4x+3y<0;
(3)x=3; (4) x2+xy+y2;
(5)x≠5; (6)x+2>y+5.
解 : (1)(2)(5)(6)是不等式; (3)(4)不是不等式.
做一做
用不等式表示:
(1)y的3倍小于8.
(2)m与10的和不小于m的一半。
(3)汛期,湖水平均每天上涨8cm。现在的水位是340cm,警戒水位是460cm。x天后湖水将超过警戒水位。
解:(1)3y<8.
(2)m+10≥
(3)8x+340>460.
课堂练习
1. 下列各式,不等式一共有______个.
① 5=9-4;
②5>-3;
③x+2≠3+x;
④2+x≥2x-1;
⑤a2+2a+1≤8.
2. 用不等式表示下列数量关系:
(1)a是负数;
(2)x比-3小;
(3)两数m与n的差不大于5.
a < 0;
x <-3;
m-n ≤5.
3
课堂练习
3.在-1,-0.5,0,0.5,1,3,7,100中,哪些能使不等式x+0.5<2成立?
解:当x=-1时,x+0.5=-0.5<右边;
当x=-0.5时,x+0.5=0<右边;
当x=0时,x+0.5=0.5<右边;
当x=0.5时,x+0.5=1<右边;
当x=1时,x+0.5=1.5<右边;
当x=3时,x+0.5=3.5>右边;
当x=7时,x+0.5=7.5>右边;
当x=100时,x+0.5=100.5>右边,所以,当x取-1,-0.5,0,0.5,1时,不等式x+0.5<2成立.
课堂练习
4.(1)雷电的温度大约是28000℃,比太阳表面温度的4.5倍还要高.设太阳表面温度为t℃,那么t应该满足怎样的关系式?
4.5t<28000
(2)黄石市某天的最高气温为+5℃,最低气温比最高气温低8℃,则这天此地气温t(℃)应该满足怎样的关系式?
-3℃≤ t ≤5℃
课堂练习
5.在通过桥洞时,我们往往会看到如图(1)所示的标志,这是限制车高的标志.你知道通过该桥洞的车高x(m)的范围吗?在通过桥面时,我们往往会看到如图(2)所示的标志,这是限制车重的标志.你知道通过该桥面的车重y(t)的范围吗?
(1)
(2)
10t
5m
x≤5m
y≤10t
总结
不等式
列不等式
概念
判断一个式子是否是不等式,主要看这个式子中是否有不等号:
____,____,____,____.
>
<
≥
≤
列不等式的关键是要审清题意,抓住“>”“<”“≥”或“≤”的本质含义.
谢谢听讲!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
