2021-2022学年高一下学期数学人教A版(2019)必修第二册8.6.3平面与平面垂直课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册8.6.3平面与平面垂直课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 556.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 21:49:51 | ||
图片预览




文档简介
(共23张PPT)
回顾:一、直线和平面垂直的判定
1.定理:如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
*2.两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面.
*3.一条直线垂直于两个平行平面中的一个,也垂直于另一个.
,
即:
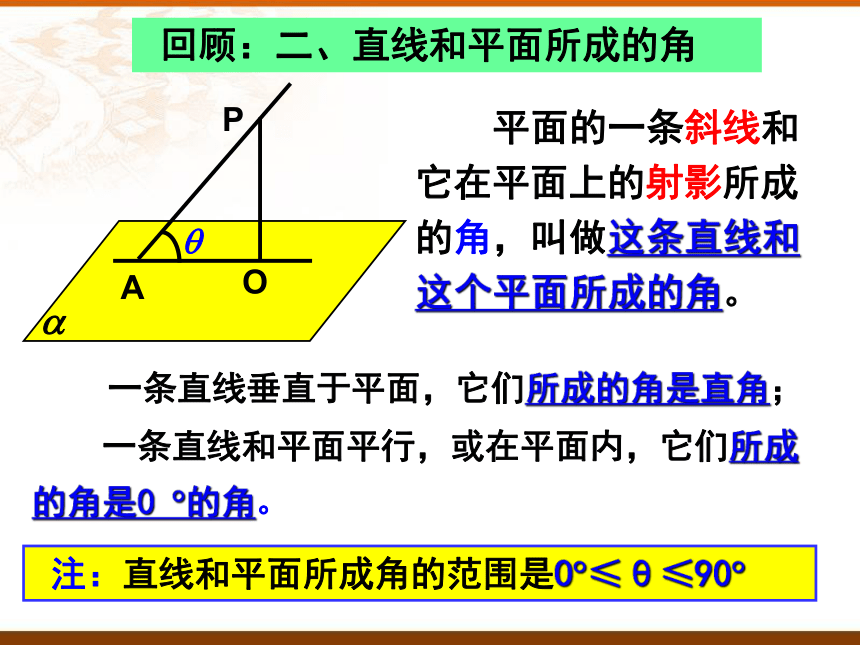
平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角。
一条直线垂直于平面,它们所成的角是直角;
一条直线和平面平行,或在平面内,它们所成的角是0 的角。
注:直线和平面所成角的范围是0 ≤θ≤90
回顾:二、直线和平面所成的角
P
A
O
定理:垂直于同一个平面的两条直线平行
符号语言:
说明:可由两条直线与一个平面垂直判定两条直线平行,性质定理揭示了“平行”与“垂直”的内在联系。
直线与平面垂直的性质1:
直线与平面垂直的性质2:
若一条直线垂直于一个平面,则该直线垂直于平面内的任意一条直线。
8.6.3 平面与平面垂直
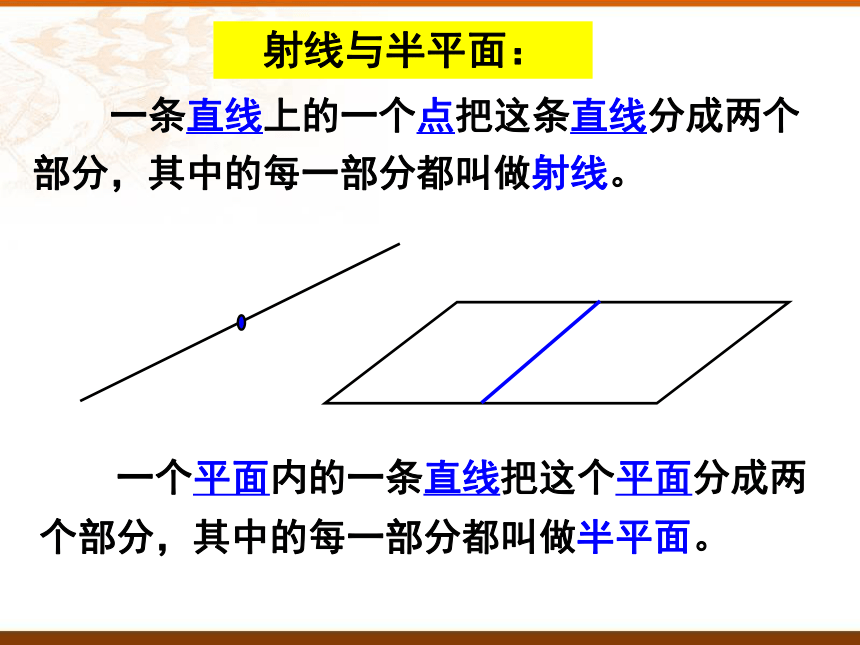
一个平面内的一条直线把这个平面分成两个部分,其中的每一部分都叫做半平面。
一条直线上的一个点把这条直线分成两个部分,其中的每一部分都叫做射线。
射线与半平面:
O
B
A
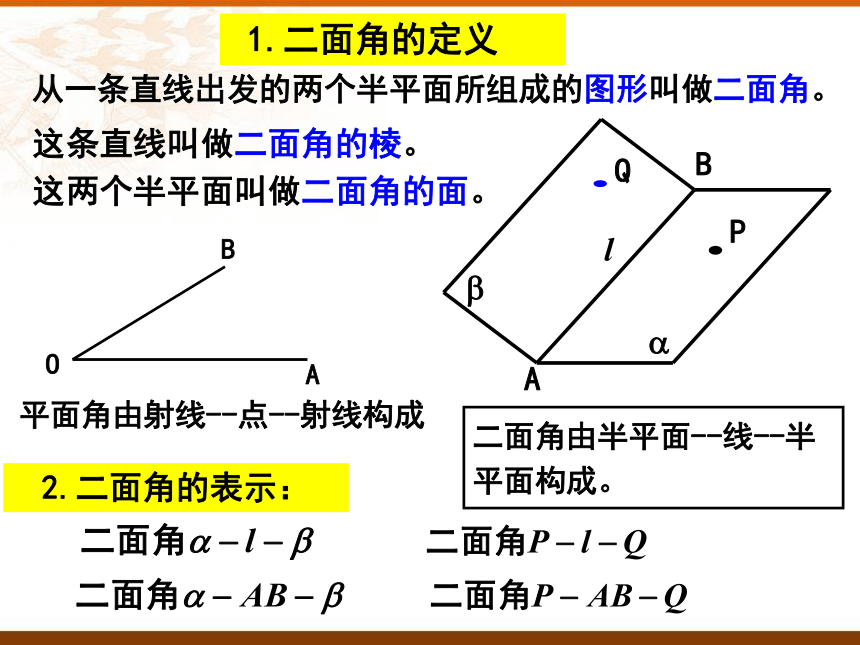
这条直线叫做二面角的棱。
平面角由射线--点--射线构成
二面角由半平面--线--半平面构成。
l
A
B
P
Q
从一条直线出发的两个半平面所组成的图形叫做二面角。
2.二面角的表示:
这两个半平面叫做二面角的面。
1.二面角的定义
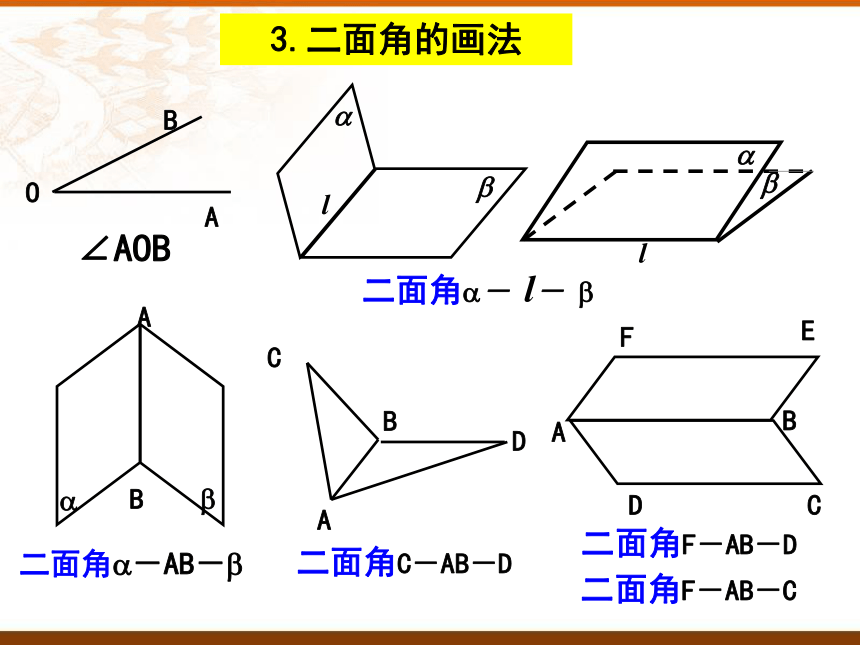
3.二面角的画法
l
A
B
二面角 -AB-
l
二面角 - l-
二面角C-AB-D
A
B
C
D
O
B
A
∠AOB
A
B
C
E
F
D
二面角F-AB-D
二面角F-AB-C
二面角的平面角:在二面角α- l -β的棱 l 上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱 l 的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角
l
O
A
B
4.二面角的度量
*(1)表示二面角的平面角时,要求“OA⊥l,OB⊥l ”;
*(2)∠AOB的大小与点O在棱l 上的位置无关;
(3)二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度;
(4)直二面角:平面角是直角的二面角叫直二面角。
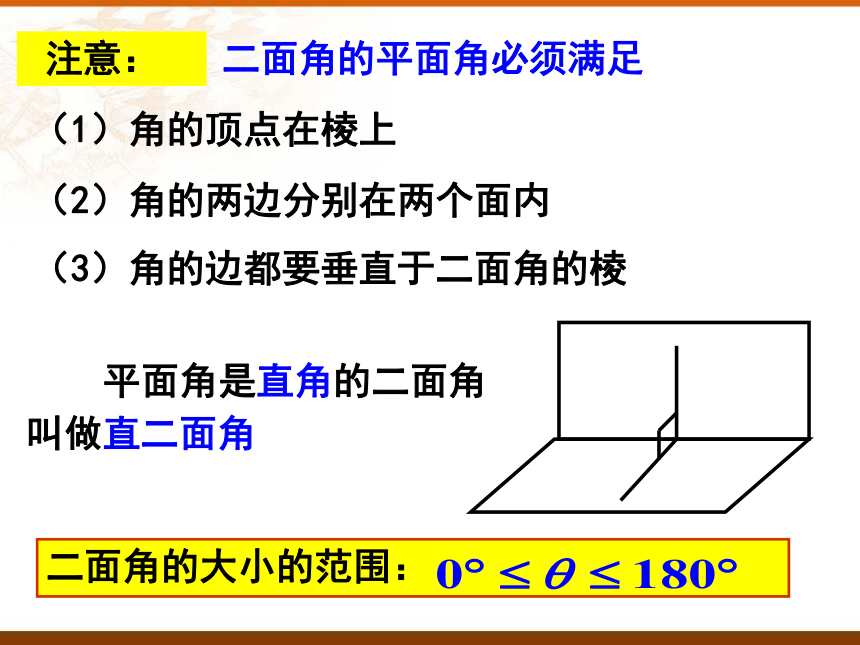
注意:
二面角的平面角必须满足
(3)角的边都要垂直于二面角的棱
(1)角的顶点在棱上
(2)角的两边分别在两个面内
平面角是直角的二面角叫做直二面角
二面角的大小的范围:
B
A
C
D
定义法:在二面角的棱上取一点(特殊点),分别在两个半平面内作棱的垂线。(等腰三角形注意做高线);
分析:因为AB=BC=CD=DA,故取BD的中点E,连接AE,CE,可知AE⊥BD,CE⊥BD,故二面角A-BD-C的平面角为∠AEC.
E
例:空间四边形ABCD中,AB=BC=CD=DA= ,对角线
BD=2,AC= ,求二面角A-BD-C的大小。
做(找)棱的垂线,证明线线垂直,指出二面角,在三角形中求角。
即:做(找)、证、指、求四环节。
求二面角的基本步骤:
二面角的求法
观察:教室相邻两个墙角与地面可以构成几个二面角?分别指出构成这些二面角的面、棱、平面角及其度数。
两个平面垂直:两个平面所成的二面角为直二面角,就说这两个平面互相垂直. 记作: α ⊥ β
演示:课本与桌面垂直
问题:
如何检测所砌的墙面和地面是否垂直?
如何检测所砌的墙面和地面是否垂直?
两个平面互相垂直的判定定理:
一个平面过另一个平面的垂线,则这两个平面垂直。
问题:
定理:如果一个平面过另一个平面的垂线,那么这两个平面垂直.
符号:
β
α
a
A
简记:线面垂直,则面面垂直
5.平面与平面垂直的判定
画法
例8:如图,AB是⊙O直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.
证明:
设⊙O所在平面为α
请问哪些平面是互相垂直的,为什么
D
A
B
C
请看课本P158:练习3,4
A1
B
C1
B1
D
C
A
D1
在以下所给正方体中,判断下列是否正确
(1)平面ADD1A1 平面ABCD;
(2)D1A AB;
(3)D1A 面ABCD
过点A可以在平面ADD1A1内作无数条直线,而这些直线满足什么条件就可以使之与平面ABCD垂直?
[探索研究]
如果两个平面互相垂直,那么在第一个平面内垂直于交线的直线,是否垂直于第二个平面呢?
证明:过B在平面β内作BE⊥CD,
A
B
α
β
C
D
E
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
二、探索研究
Ⅰ. 观察实验
观察两垂直平面中,一个平面内的直线与另一个平面的有哪些位置关系
Ⅱ.概括结论
平面与平面垂直的性质定理:
b
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
简述为:
面面垂直
线面垂直
该命题正确吗?
符号表示:
a
a
β
α
P
思考:设平面 ⊥平面 ,点P在平面 内,过点P作平面 的垂线a,直线a与平面 具有什么位置关系
β
α
P
直线a在平面 内
c
c
面面垂直
线面垂直
性质定理
判定定理
一个平面过另一个平面的垂线,则这两个平面垂直.
两个平面垂直,则一个平面内垂直于交线的
直线与另一个平面垂直.
线面垂直
线线垂直
面面垂直
三、小结
请看课本P161:练习1,2
回顾:一、直线和平面垂直的判定
1.定理:如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
*2.两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面.
*3.一条直线垂直于两个平行平面中的一个,也垂直于另一个.
,
即:
平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角。
一条直线垂直于平面,它们所成的角是直角;
一条直线和平面平行,或在平面内,它们所成的角是0 的角。
注:直线和平面所成角的范围是0 ≤θ≤90
回顾:二、直线和平面所成的角
P
A
O
定理:垂直于同一个平面的两条直线平行
符号语言:
说明:可由两条直线与一个平面垂直判定两条直线平行,性质定理揭示了“平行”与“垂直”的内在联系。
直线与平面垂直的性质1:
直线与平面垂直的性质2:
若一条直线垂直于一个平面,则该直线垂直于平面内的任意一条直线。
8.6.3 平面与平面垂直
一个平面内的一条直线把这个平面分成两个部分,其中的每一部分都叫做半平面。
一条直线上的一个点把这条直线分成两个部分,其中的每一部分都叫做射线。
射线与半平面:
O
B
A
这条直线叫做二面角的棱。
平面角由射线--点--射线构成
二面角由半平面--线--半平面构成。
l
A
B
P
Q
从一条直线出发的两个半平面所组成的图形叫做二面角。
2.二面角的表示:
这两个半平面叫做二面角的面。
1.二面角的定义
3.二面角的画法
l
A
B
二面角 -AB-
l
二面角 - l-
二面角C-AB-D
A
B
C
D
O
B
A
∠AOB
A
B
C
E
F
D
二面角F-AB-D
二面角F-AB-C
二面角的平面角:在二面角α- l -β的棱 l 上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱 l 的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角
l
O
A
B
4.二面角的度量
*(1)表示二面角的平面角时,要求“OA⊥l,OB⊥l ”;
*(2)∠AOB的大小与点O在棱l 上的位置无关;
(3)二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度;
(4)直二面角:平面角是直角的二面角叫直二面角。
注意:
二面角的平面角必须满足
(3)角的边都要垂直于二面角的棱
(1)角的顶点在棱上
(2)角的两边分别在两个面内
平面角是直角的二面角叫做直二面角
二面角的大小的范围:
B
A
C
D
定义法:在二面角的棱上取一点(特殊点),分别在两个半平面内作棱的垂线。(等腰三角形注意做高线);
分析:因为AB=BC=CD=DA,故取BD的中点E,连接AE,CE,可知AE⊥BD,CE⊥BD,故二面角A-BD-C的平面角为∠AEC.
E
例:空间四边形ABCD中,AB=BC=CD=DA= ,对角线
BD=2,AC= ,求二面角A-BD-C的大小。
做(找)棱的垂线,证明线线垂直,指出二面角,在三角形中求角。
即:做(找)、证、指、求四环节。
求二面角的基本步骤:
二面角的求法
观察:教室相邻两个墙角与地面可以构成几个二面角?分别指出构成这些二面角的面、棱、平面角及其度数。
两个平面垂直:两个平面所成的二面角为直二面角,就说这两个平面互相垂直. 记作: α ⊥ β
演示:课本与桌面垂直
问题:
如何检测所砌的墙面和地面是否垂直?
如何检测所砌的墙面和地面是否垂直?
两个平面互相垂直的判定定理:
一个平面过另一个平面的垂线,则这两个平面垂直。
问题:
定理:如果一个平面过另一个平面的垂线,那么这两个平面垂直.
符号:
β
α
a
A
简记:线面垂直,则面面垂直
5.平面与平面垂直的判定
画法
例8:如图,AB是⊙O直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.
证明:
设⊙O所在平面为α
请问哪些平面是互相垂直的,为什么
D
A
B
C
请看课本P158:练习3,4
A1
B
C1
B1
D
C
A
D1
在以下所给正方体中,判断下列是否正确
(1)平面ADD1A1 平面ABCD;
(2)D1A AB;
(3)D1A 面ABCD
过点A可以在平面ADD1A1内作无数条直线,而这些直线满足什么条件就可以使之与平面ABCD垂直?
[探索研究]
如果两个平面互相垂直,那么在第一个平面内垂直于交线的直线,是否垂直于第二个平面呢?
证明:过B在平面β内作BE⊥CD,
A
B
α
β
C
D
E
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
二、探索研究
Ⅰ. 观察实验
观察两垂直平面中,一个平面内的直线与另一个平面的有哪些位置关系
Ⅱ.概括结论
平面与平面垂直的性质定理:
b
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
简述为:
面面垂直
线面垂直
该命题正确吗?
符号表示:
a
a
β
α
P
思考:设平面 ⊥平面 ,点P在平面 内,过点P作平面 的垂线a,直线a与平面 具有什么位置关系
β
α
P
直线a在平面 内
c
c
面面垂直
线面垂直
性质定理
判定定理
一个平面过另一个平面的垂线,则这两个平面垂直.
两个平面垂直,则一个平面内垂直于交线的
直线与另一个平面垂直.
线面垂直
线线垂直
面面垂直
三、小结
请看课本P161:练习1,2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
