北师大版数学九下1.1锐角三角函数 教案
文档属性
| 名称 | 北师大版数学九下1.1锐角三角函数 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 19:24:46 | ||
图片预览


文档简介
“§1.1锐角三角函数 第一课时 正切”教学设计
教学目标:
1.经历探索刻画梯子倾斜程度的过程,理解正切的概念,感受正切与现实生活的联系.
2.了解坡度、坡角等概念,并能用正切进行简单的计算.
3.逐步学会利用数形结合,从特殊到一般、转化等数学思想分析问题和解决问题.
教学重点与难点:
重点:
1.理解正切的概念.
难点:
1.理解正切为什么能够刻画梯子的倾斜程度.
教法与学法指导:
试验探究法.通过实际生活中的现象和例子,用多媒体进行展示,进而引导学生进行分析讨论,总结出正切的概念,再结合适量的练习加以巩固提高;鼓励学生从生活中发现数学的重要性,课堂上以独立发现和总结规律为主,同时配合小组讨论和探究,争取正确地掌握正切的概念,以及运用上述知识解决实际问题.
课前准备:多媒体课件.
三、教学过程
(一)联系生活,导入新课
教师用多媒体展示生活中一些与梯子相关的图片后,导人新课:
同学们!梯子是我们日常生活中常用的工具,在使用梯子的时候,有时需要放得陡一些,有时需要放得缓一些,那么我们该如何刻画梯子的倾斜程度呢?
生:倾斜角大,梯子就陡;倾斜角小,梯子就缓.
师:是的,在实际问题中,有时我们不方便测量倾斜角,有时不容易准确测量倾斜角,那我们又该如何刻画梯子的倾斜程度呢?今天,我们对这个问题继续进行深入研究(板书课题).
活动目的:由学生熟悉的梯子引入新课,紧扣课题,从而自然过渡到下面的探究活动.
(二)研究问题,探索新知
1.做一做
教师用多媒体展示图1.
图1中,梯子AB和EF哪个更陡?你是怎样剡断的?
师:请同学们独立思考后举手回答.
生:因为这两个梯子的竖直高度相同,而梯子EF的水平宽度比梯子AB的小,所以梯子EF更陡.
师:很好.
教师用多媒体展示图2.
图2中,梯子AB和EF哪个更陡?你是怎样判断的?
生:因为这丽个梯子的水平宽度相同,而梯子EF的竖直高度比梯子AB的小,所以梯子AB更陡.
教师用多媒体展示图3.
图3中,梯子AB和EF哪个更陡?你是怎样判断的?
生:(七台讲解)由图可知,在这两个三角形中,两边对应成比例,且夹角相等,所以这两个三角形相似,因此,梯子AB与地面的夹角和梯子EF与地面的夹角相等,所以两个梯子一样陡,
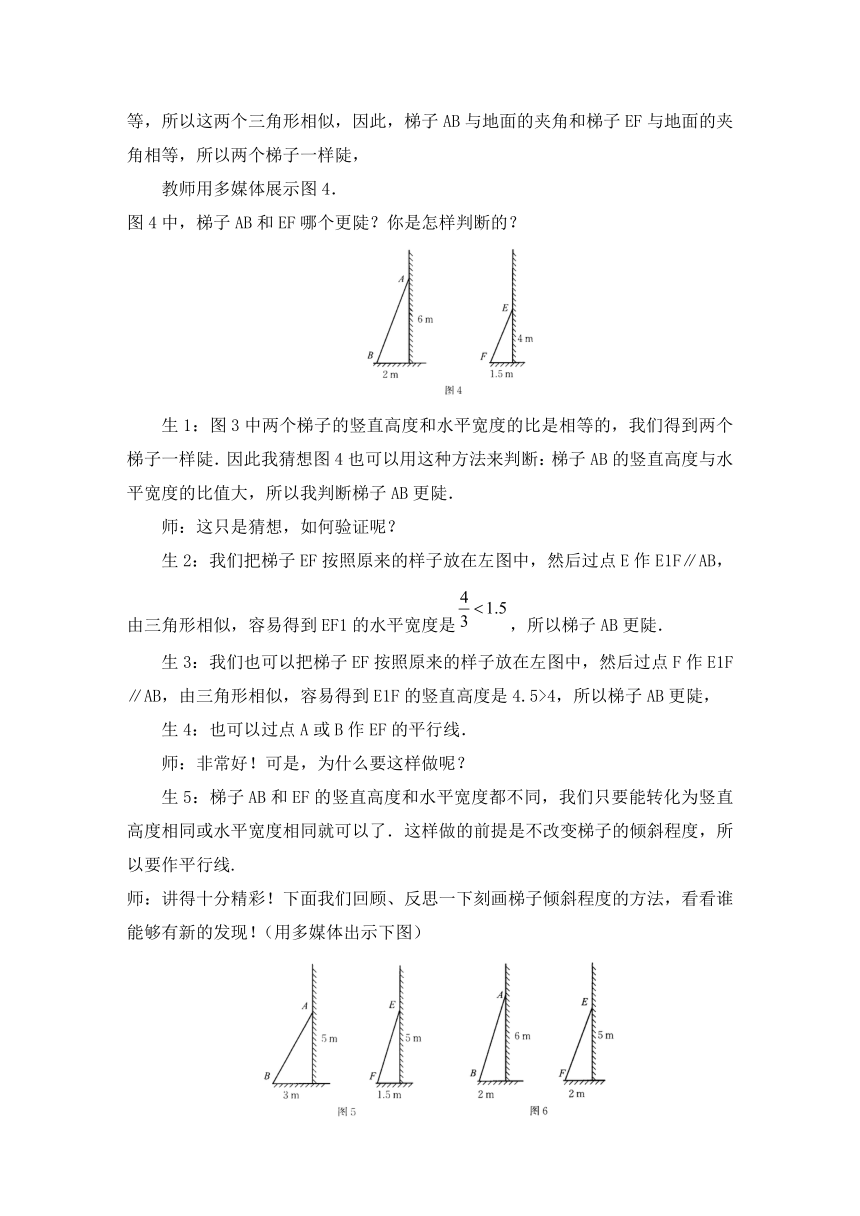
教师用多媒体展示图4.
图4中,梯子AB和EF哪个更陡?你是怎样判断的?
生1:图3中两个梯子的竖直高度和水平宽度的比是相等的,我们得到两个梯子一样陡.因此我猜想图4也可以用这种方法来判断:梯子AB的竖直高度与水平宽度的比值大,所以我判断梯子AB更陡.
师:这只是猜想,如何验证呢?
生2:我们把梯子EF按照原来的样子放在左图中,然后过点E作E1F∥AB,由三角形相似,容易得到EF1的水平宽度是,所以梯子AB更陡.
生3:我们也可以把梯子EF按照原来的样子放在左图中,然后过点F作E1F∥AB,由三角形相似,容易得到E1F的竖直高度是4.5>4,所以梯子AB更陡,
生4:也可以过点A或B作EF的平行线.
师:非常好!可是,为什么要这样做呢?
生5:梯子AB和EF的竖直高度和水平宽度都不同,我们只要能转化为竖直高度相同或水平宽度相同就可以了.这样做的前提是不改变梯子的倾斜程度,所以要作平行线.
师:讲得十分精彩!下面我们回顾、反思一下刻画梯子倾斜程度的方法,看看谁能够有新的发现!(用多媒体出示下图)
生:归纳各种情况,可以发现:竖直高度和水平宽度的比值越大,梯子越陡.
活动目的:从图1到图4,四个问题由浅入深,由简单到复杂,步步深入,环环相扣,引人人胜.学生们在用生活常识和有关知识解决问题时,非常自然地感悟了用“竖直高度和水平宽度的比值”来刻画梯子的倾斜程度.
2.想一想
如图9,小明想通过测量B1C1及A1C1,算出它们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量B2C2及A2C2,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?
生:同意.
师:为什么?
生1:显然Rt△AB1C1和Rt△AB2C2相似,所以和相等.
师:如果改变B2的位置呢?
生2:B2无论在什么位置,Rt△AB1C1和Rt△AB2C2都相似,所以和相等.
师:由此你能得出什么结论?
生3:当梯子的倾斜角一定时,它的竖直高度和水平宽度的比值就一定.
活动目的:此环节旨在说明当倾斜角确定时,其对边与邻边的比值便随之确定,也就是说,这一比值只与倾斜角有关,而与直角三角形的大小无关.
3.讲一讲
师:在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA.即
(教师强调锐角A的对边与邻边).
师:谁来说说图10中∠B的正切等于什么?
生:
师:很好.
活动目的:理解正切的概念和表示,理解tanA是一个抽象的符号,它代表一个“比”或“比值”.
4.议一议
师:在图9中,梯子的倾斜程度与tanA有什么关系?
生:tanA的值越大,梯子越陡.
活动目的:旨在让学生理解梯子的倾斜程度与倾斜角的正切之间的关系.
5.想一想
师:我们知道,可以用梯子倾斜角的正切刻画梯子的倾斜程度,那么怎样刻画山坡的倾斜程度呢?
生:可以用坡面和水平面所成的角来刻画,也可以用坡面的铅直高度与水平宽度的比来刻画.
师:太对了,我们把前者叫做坡角,后者叫做坡度(或坡比).
活动目的:旨在让学生理解坡角和坡度.
例如图11,甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
解:甲梯中,
乙梯中,
因为>,所以甲梯更陡.
活动目的:例题由学生独立完成,合作交流,订正完善,规范步骤.
(三)巩固练习,形成技能
随堂练习第1,2题;习题1.1第4题.
活动目的:通过基本的练习,进一步加强学生对正切和坡度的理解,形成相应的技能.
(四)课堂小结
教师引导学生畅所欲言地谈谈本节课的收获:
1.经历了探索梯子倾斜程度的过程;
2.理解了正切和坡度的概念;
3.了解了tan A的值越大,梯子(坡)越陡;
4.体会了相关的数学思想方法:从特殊到一般、转化.
活动目的:通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯.
(五)布置作业
1.书面作业:习题1.1第1,2题;
2.弹性作业:习题1.1第3题.
活动目的:如此布置作业,既巩同知识技能,又减轻学生负担。
板书设计:
教学反思:
本节课是三角函数部分的第一节概念教学,教材内容比较抽象,学生以前从没接触过三角函数,尤其是涉及到以角度为自变量这样特殊的函数概念,学生不易理解.为此结合初中学生身心发展的特点,这节课运用了实验教学、直观教学,唤起和加深学生对教学内容的体会和了解,并培养和发展学生的观察、思维能力,这是贯彻“从生动的直观到抽象的思维,并从抽象的思维到实践”的基本认识规律,运用好这些直观教学,能使学生学习数学的过程成为积极的愉快的和富有想象的过程,使学习数学的过程不再是令人生畏的过程.概念教学由学生熟悉的实例入手,引导学生观察、分析、动手、动脑、动口多种感官参与,并组织学生积极参与小组成员间合作交流.通过特殊到一般、具体到抽象的探索过程,紧紧围绕着函数概念,引出正切概念,再通过相应的典型题组练习巩固概念.并且在教学过程中,注重了阶段性的反思小结,使学生能够及时总结知识和方法.
1.1 从梯子的倾斜程度谈起(1)
一、正切的定义 二、例题 学生练习
tanA=.
三、坡度
当直角三角形中的锐角确定之后,它的对边与邻边之比也随之确定.
教学目标:
1.经历探索刻画梯子倾斜程度的过程,理解正切的概念,感受正切与现实生活的联系.
2.了解坡度、坡角等概念,并能用正切进行简单的计算.
3.逐步学会利用数形结合,从特殊到一般、转化等数学思想分析问题和解决问题.
教学重点与难点:
重点:
1.理解正切的概念.
难点:
1.理解正切为什么能够刻画梯子的倾斜程度.
教法与学法指导:
试验探究法.通过实际生活中的现象和例子,用多媒体进行展示,进而引导学生进行分析讨论,总结出正切的概念,再结合适量的练习加以巩固提高;鼓励学生从生活中发现数学的重要性,课堂上以独立发现和总结规律为主,同时配合小组讨论和探究,争取正确地掌握正切的概念,以及运用上述知识解决实际问题.
课前准备:多媒体课件.
三、教学过程
(一)联系生活,导入新课
教师用多媒体展示生活中一些与梯子相关的图片后,导人新课:
同学们!梯子是我们日常生活中常用的工具,在使用梯子的时候,有时需要放得陡一些,有时需要放得缓一些,那么我们该如何刻画梯子的倾斜程度呢?
生:倾斜角大,梯子就陡;倾斜角小,梯子就缓.
师:是的,在实际问题中,有时我们不方便测量倾斜角,有时不容易准确测量倾斜角,那我们又该如何刻画梯子的倾斜程度呢?今天,我们对这个问题继续进行深入研究(板书课题).
活动目的:由学生熟悉的梯子引入新课,紧扣课题,从而自然过渡到下面的探究活动.
(二)研究问题,探索新知
1.做一做
教师用多媒体展示图1.
图1中,梯子AB和EF哪个更陡?你是怎样剡断的?
师:请同学们独立思考后举手回答.
生:因为这两个梯子的竖直高度相同,而梯子EF的水平宽度比梯子AB的小,所以梯子EF更陡.
师:很好.
教师用多媒体展示图2.
图2中,梯子AB和EF哪个更陡?你是怎样判断的?
生:因为这丽个梯子的水平宽度相同,而梯子EF的竖直高度比梯子AB的小,所以梯子AB更陡.
教师用多媒体展示图3.
图3中,梯子AB和EF哪个更陡?你是怎样判断的?
生:(七台讲解)由图可知,在这两个三角形中,两边对应成比例,且夹角相等,所以这两个三角形相似,因此,梯子AB与地面的夹角和梯子EF与地面的夹角相等,所以两个梯子一样陡,
教师用多媒体展示图4.
图4中,梯子AB和EF哪个更陡?你是怎样判断的?
生1:图3中两个梯子的竖直高度和水平宽度的比是相等的,我们得到两个梯子一样陡.因此我猜想图4也可以用这种方法来判断:梯子AB的竖直高度与水平宽度的比值大,所以我判断梯子AB更陡.
师:这只是猜想,如何验证呢?
生2:我们把梯子EF按照原来的样子放在左图中,然后过点E作E1F∥AB,由三角形相似,容易得到EF1的水平宽度是,所以梯子AB更陡.
生3:我们也可以把梯子EF按照原来的样子放在左图中,然后过点F作E1F∥AB,由三角形相似,容易得到E1F的竖直高度是4.5>4,所以梯子AB更陡,
生4:也可以过点A或B作EF的平行线.
师:非常好!可是,为什么要这样做呢?
生5:梯子AB和EF的竖直高度和水平宽度都不同,我们只要能转化为竖直高度相同或水平宽度相同就可以了.这样做的前提是不改变梯子的倾斜程度,所以要作平行线.
师:讲得十分精彩!下面我们回顾、反思一下刻画梯子倾斜程度的方法,看看谁能够有新的发现!(用多媒体出示下图)
生:归纳各种情况,可以发现:竖直高度和水平宽度的比值越大,梯子越陡.
活动目的:从图1到图4,四个问题由浅入深,由简单到复杂,步步深入,环环相扣,引人人胜.学生们在用生活常识和有关知识解决问题时,非常自然地感悟了用“竖直高度和水平宽度的比值”来刻画梯子的倾斜程度.
2.想一想
如图9,小明想通过测量B1C1及A1C1,算出它们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量B2C2及A2C2,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?
生:同意.
师:为什么?
生1:显然Rt△AB1C1和Rt△AB2C2相似,所以和相等.
师:如果改变B2的位置呢?
生2:B2无论在什么位置,Rt△AB1C1和Rt△AB2C2都相似,所以和相等.
师:由此你能得出什么结论?
生3:当梯子的倾斜角一定时,它的竖直高度和水平宽度的比值就一定.
活动目的:此环节旨在说明当倾斜角确定时,其对边与邻边的比值便随之确定,也就是说,这一比值只与倾斜角有关,而与直角三角形的大小无关.
3.讲一讲
师:在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA.即
(教师强调锐角A的对边与邻边).
师:谁来说说图10中∠B的正切等于什么?
生:
师:很好.
活动目的:理解正切的概念和表示,理解tanA是一个抽象的符号,它代表一个“比”或“比值”.
4.议一议
师:在图9中,梯子的倾斜程度与tanA有什么关系?
生:tanA的值越大,梯子越陡.
活动目的:旨在让学生理解梯子的倾斜程度与倾斜角的正切之间的关系.
5.想一想
师:我们知道,可以用梯子倾斜角的正切刻画梯子的倾斜程度,那么怎样刻画山坡的倾斜程度呢?
生:可以用坡面和水平面所成的角来刻画,也可以用坡面的铅直高度与水平宽度的比来刻画.
师:太对了,我们把前者叫做坡角,后者叫做坡度(或坡比).
活动目的:旨在让学生理解坡角和坡度.
例如图11,甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
解:甲梯中,
乙梯中,
因为>,所以甲梯更陡.
活动目的:例题由学生独立完成,合作交流,订正完善,规范步骤.
(三)巩固练习,形成技能
随堂练习第1,2题;习题1.1第4题.
活动目的:通过基本的练习,进一步加强学生对正切和坡度的理解,形成相应的技能.
(四)课堂小结
教师引导学生畅所欲言地谈谈本节课的收获:
1.经历了探索梯子倾斜程度的过程;
2.理解了正切和坡度的概念;
3.了解了tan A的值越大,梯子(坡)越陡;
4.体会了相关的数学思想方法:从特殊到一般、转化.
活动目的:通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯.
(五)布置作业
1.书面作业:习题1.1第1,2题;
2.弹性作业:习题1.1第3题.
活动目的:如此布置作业,既巩同知识技能,又减轻学生负担。
板书设计:
教学反思:
本节课是三角函数部分的第一节概念教学,教材内容比较抽象,学生以前从没接触过三角函数,尤其是涉及到以角度为自变量这样特殊的函数概念,学生不易理解.为此结合初中学生身心发展的特点,这节课运用了实验教学、直观教学,唤起和加深学生对教学内容的体会和了解,并培养和发展学生的观察、思维能力,这是贯彻“从生动的直观到抽象的思维,并从抽象的思维到实践”的基本认识规律,运用好这些直观教学,能使学生学习数学的过程成为积极的愉快的和富有想象的过程,使学习数学的过程不再是令人生畏的过程.概念教学由学生熟悉的实例入手,引导学生观察、分析、动手、动脑、动口多种感官参与,并组织学生积极参与小组成员间合作交流.通过特殊到一般、具体到抽象的探索过程,紧紧围绕着函数概念,引出正切概念,再通过相应的典型题组练习巩固概念.并且在教学过程中,注重了阶段性的反思小结,使学生能够及时总结知识和方法.
1.1 从梯子的倾斜程度谈起(1)
一、正切的定义 二、例题 学生练习
tanA=.
三、坡度
当直角三角形中的锐角确定之后,它的对边与邻边之比也随之确定.
