北师大版数学九下1.1锐角三角函数 课件 (共34张PPT)
文档属性
| 名称 | 北师大版数学九下1.1锐角三角函数 课件 (共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览




文档简介
(共34张PPT)
第一章 直角三角形的边角关系
1.1 锐角三角函数
第1课时 正切
引言:直角三角形的边角关系,我们已经研究过什么?还可以研究什么?
两锐角互余
勾股定理
1.经历探索刻画梯子倾斜程度的过程,理解正切的概念,感受正切与现实生活的联系.
2.了解坡度、坡角等概念,并能用正切进行简单的计算.
3.逐步学会利用数形结合,从特殊到一般、转化等数学思想分析问题和解决问题.
重点:
1.理解正切的概念.
难点:
1.理解正切为什么能够刻画梯子的倾斜程度.
生活中的梯子
导入新课
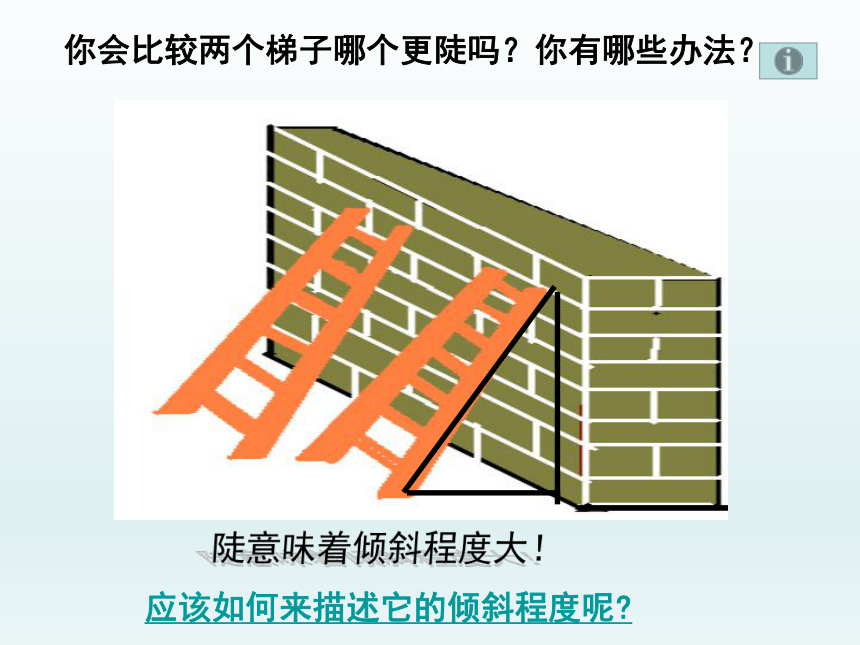
你会比较两个梯子哪个更陡吗?你有哪些办法?
应该如何来描述它的倾斜程度呢
陡意味着倾斜程度大!
知识储备
陡了还是缓了?
注:单击文字部分可以反复播放动画
铅直高度
水平宽度
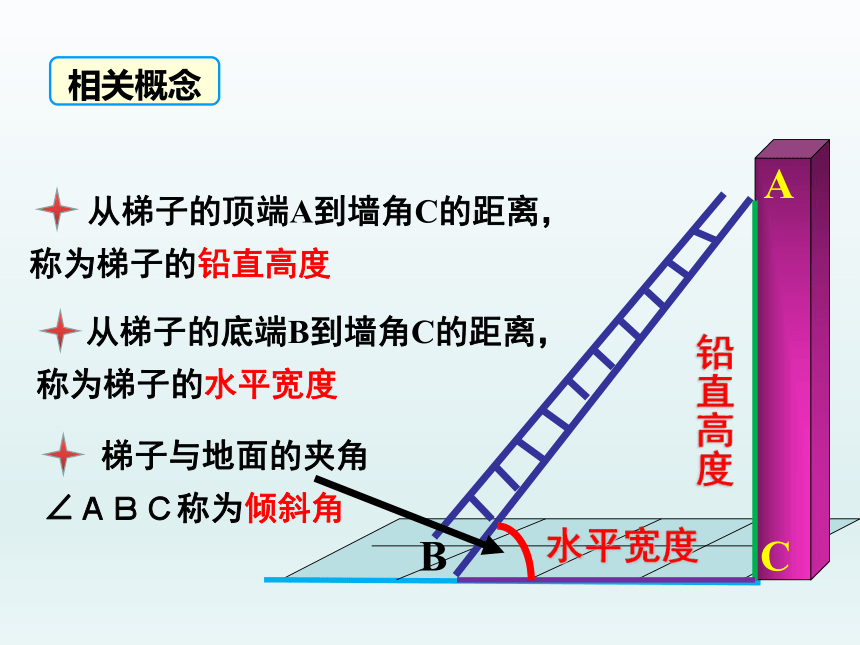
梯子与地面的夹角∠ABC称为倾斜角
从梯子的顶端A到墙角C的距离,称为梯子的铅直高度
从梯子的底端B到墙角C的距离,称为梯子的水平宽度
A
C
B
相关概念
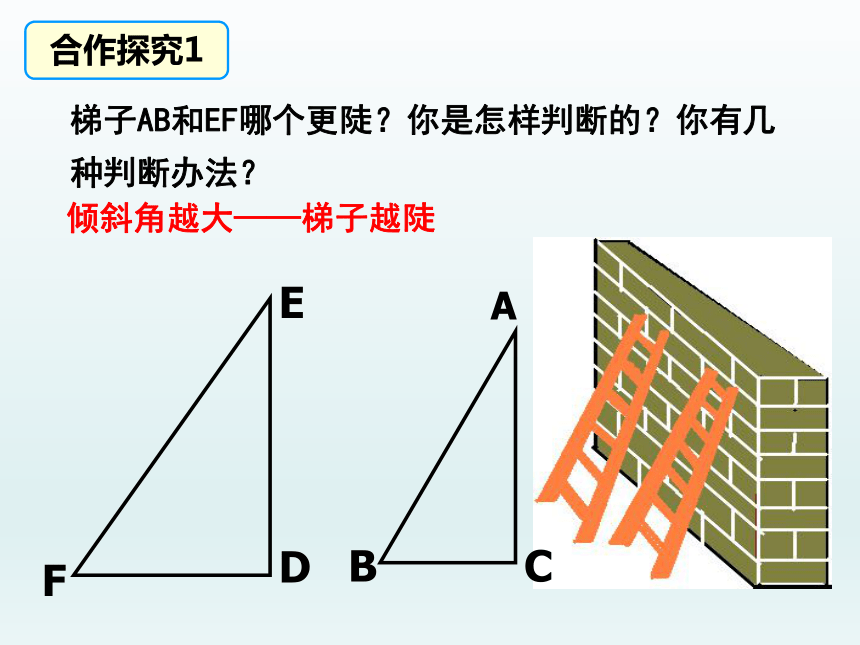
梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断办法?
合作探究1
A
B
C
D
E
F
倾斜角越大——梯子越陡
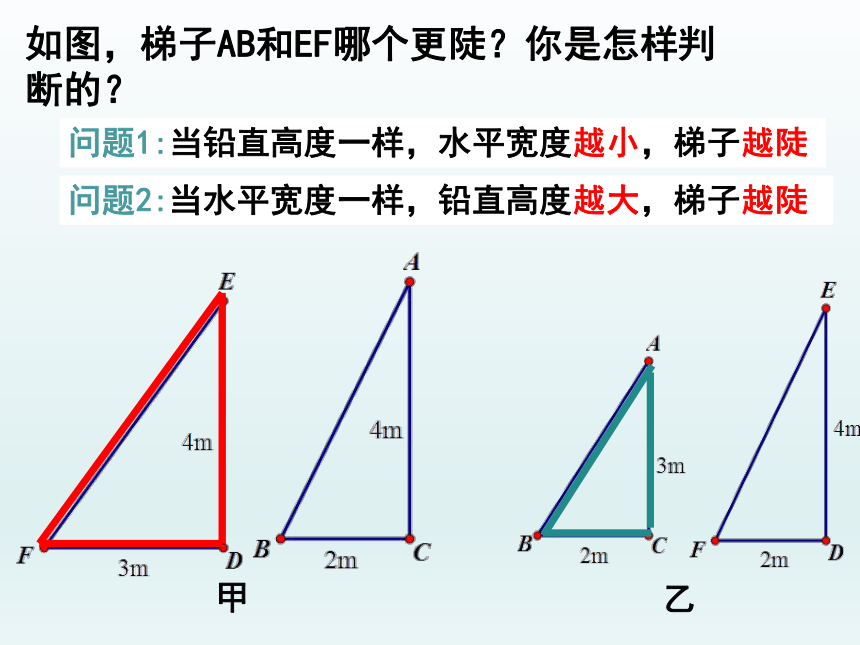
如图,梯子AB和EF哪个更陡?你是怎样判断的?
问题1:当铅直高度一样,水平宽度越小,梯子越陡
问题2:当水平宽度一样,铅直高度越大,梯子越陡
甲
乙
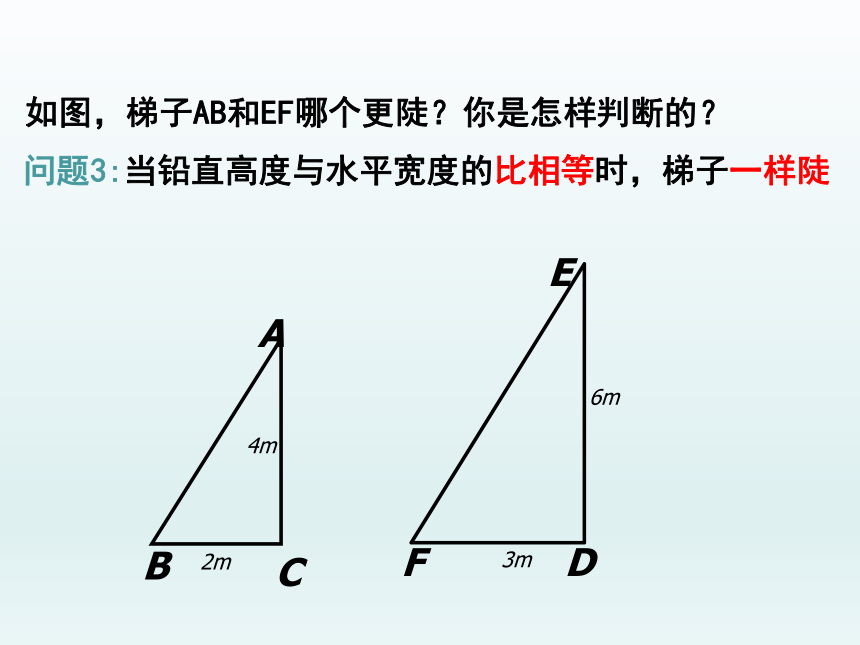
如图,梯子AB和EF哪个更陡?你是怎样判断的?
问题3:当铅直高度与水平宽度的比相等时,梯子一样陡
3m
6m
D
E
F
C
2m
B
4m
A
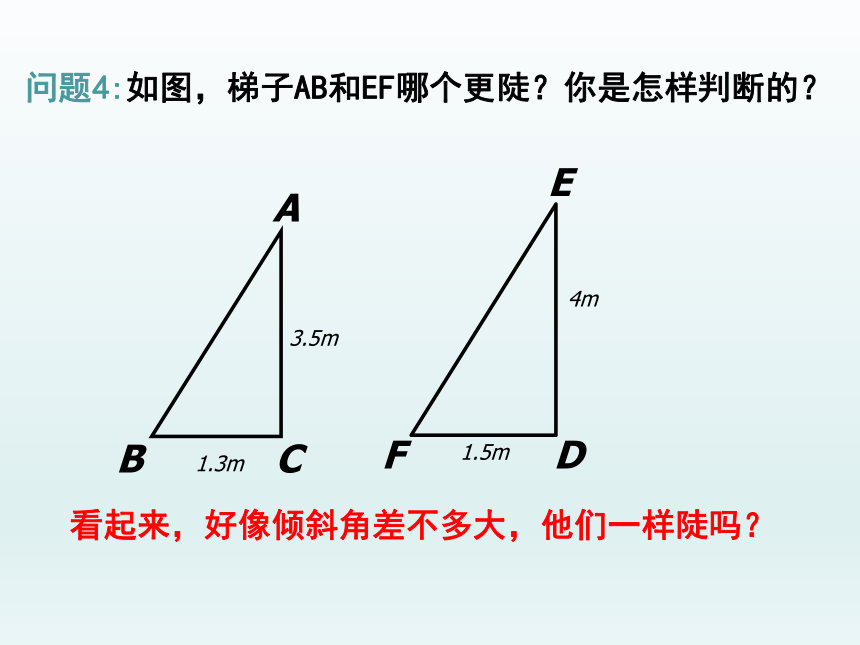
问题4:如图,梯子AB和EF哪个更陡?你是怎样判断的?
1.5m
4m
D
E
F
C
1.3m
B
3.5m
A
看起来,好像倾斜角差不多大,他们一样陡吗?
思考:
当铅直高度与水平宽度的比不相等时,
梯子倾斜程度与铅直高度与水平宽度的比有什么关系呢?
合作探究2
6m
2m
合作探究2
问题5:(1)在这个过程中,倾斜角,铅直高度,水平宽度它们是怎么变化的呢?
问题5:你有几种方法比较梯子AB和EF哪个更陡?
当铅直高度与水平宽度的比越大,梯子越陡.
3m
2m
6m
5m
A
B
C
D
E
F
倾斜角越大,梯子越陡.
判断梯子是否更陡,有如下方法:
1.可以利用倾斜角的大小比较:倾斜角越大,梯子越陡.
2.可以利用倾斜角的对边与邻边的比值大小来判断:比值越大,梯子越陡.
要点归纳
如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度;
而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子的倾斜程度.
你同意小亮的看法吗
想一想
A
B1
C1
C2
B2
(1)Rt△AB1C1和Rt△AB2C2有什么关系
(2) 和 有什么关系
(3)如果改变点B2在梯子上的位置,这种关系还成立吗?
Rt△AB1C1 ∽Rt△AB2C2
合作探究3
A
B1
C1
C2
B2
(1)Rt△AB1C1和Rt△AB2C2有什么关系
(2) 和 有什么关系
(3)如果改变点B2在梯子上的位置,这种关系还成立吗?
Rt△AB1C1 ∽Rt△AB2C2
合作探究3
A
B1
C1
C2
B2
(1)Rt△AB1C1和Rt△AB2C2有什么关系
(2) 和 有什么关系
(3)如果改变点B2在梯子上的位置,这种关系还成立吗?
Rt△AB1C1 ∽Rt△AB2C2
合作探究3
A
B1
C1
C2
B2
(1)Rt△AB1C1和Rt△AB2C2有什么关系
(2) 和 有什么关系
(3)如果改变点B2在梯子上的位置,这种关系还成立吗?
Rt△AB1C1 ∽Rt△AB2C2
∠A不变的情况下,从任何位置测出的梯子的铅直高度与水平宽度的比值都是一定的.
合作探究3
当倾斜角确定时,它的对边与邻边的比值也随之确定的,即:这个比值只与倾斜角的大小有关,而与直角三角形的大小无关.
要点归纳
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切(tangent,音标:[ t nd nt] ),记作tanA,
即
A
B
C
∠A的对边
∠A的邻边
┌
tanA=
结论:∠A越大,tanA的值越大,梯子越陡.
引入新知
定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的,∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。对于三个大写字母或者数字表示的角则不能省略角的符号.即∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA﹥0且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序).
4)tanA不表示“tan”乘以“A ”.
例1: 下图表示两个自动扶梯,哪一个自动扶梯比较陡
解:甲梯中,
β
6m
┐
乙
8m
α
5m
┌
甲
13m
乙梯中,
∵tanβ>tanα,∴乙梯更陡.
提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.
典例精析
1.判断正误
(1)如图 (1)
( ).
(2)如图 (2)
( ).
(3)如图 (2)
( ).
(4)如图 (2)
( ).
(5)如图 (2)
( ).
×
×
×
×
A
B
C
(1)
┍
A
B
C
7m
10m
(2)
√
练一练
2. 在Rt△ABC中,∠C=90°,AC=7,BC=5,则 tan A=______,tan B =______.
练一练
互余两锐角的正切值互为倒数.
3.下图中∠ACB=90°,CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.
A
B
C
D
(1) tanA =
=
AC
( )
CD
( )
(2) tanB=
=
BC
( )
CD
( )
BC
AD
BD
AC
5.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
4.已知∠A,∠B为锐角,
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.
=
=
tanA的大小只与∠A的大小有关,而与直角三角形的边长无关
6.在等腰△ABC中, AB=AC=13, BC=10,求tanB.
提示:过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.
A
C
B
┌
D
解:如图,过点A作AD⊥BC于点D,
∴在Rt△ABD中,
易知BD=5,AD=12.
正切通常也用来描述山坡的坡度.
坡度、坡角
例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度(即tanα)就是:
坡角:坡面与水平面的夹角α称为坡角;
坡度(坡比):坡面的铅直高度与水平宽度的比称
为坡度(或坡比),即坡度等于坡角的正切.
100m
60m
┌
α
概念学习
坡度越大,坡角越大,坡面就越陡.
例2 如图所示,梯形护坡石坝的斜坡AB的坡度为1∶3,坝高BC=2米,则斜坡AB的长是( )
解析:∵∠ACB=90°,坡度为1∶3,
B
方法总结:理解坡度的概念是解决与坡度有关的计算题的关键.
∵BC=2米,∴AC=3BC=3×2=6(米).
课堂小结
正切
定义
坡度
∠A越大,tanA越大,
梯子越陡
与梯子倾斜程度的关系
作业:
课本第4页
必做:随堂练习第一题,第二题
选做:习题1.1 知识技能
同学们,愿你们学有所获!
第一章 直角三角形的边角关系
1.1 锐角三角函数
第1课时 正切
引言:直角三角形的边角关系,我们已经研究过什么?还可以研究什么?
两锐角互余
勾股定理
1.经历探索刻画梯子倾斜程度的过程,理解正切的概念,感受正切与现实生活的联系.
2.了解坡度、坡角等概念,并能用正切进行简单的计算.
3.逐步学会利用数形结合,从特殊到一般、转化等数学思想分析问题和解决问题.
重点:
1.理解正切的概念.
难点:
1.理解正切为什么能够刻画梯子的倾斜程度.
生活中的梯子
导入新课
你会比较两个梯子哪个更陡吗?你有哪些办法?
应该如何来描述它的倾斜程度呢
陡意味着倾斜程度大!
知识储备
陡了还是缓了?
注:单击文字部分可以反复播放动画
铅直高度
水平宽度
梯子与地面的夹角∠ABC称为倾斜角
从梯子的顶端A到墙角C的距离,称为梯子的铅直高度
从梯子的底端B到墙角C的距离,称为梯子的水平宽度
A
C
B
相关概念
梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断办法?
合作探究1
A
B
C
D
E
F
倾斜角越大——梯子越陡
如图,梯子AB和EF哪个更陡?你是怎样判断的?
问题1:当铅直高度一样,水平宽度越小,梯子越陡
问题2:当水平宽度一样,铅直高度越大,梯子越陡
甲
乙
如图,梯子AB和EF哪个更陡?你是怎样判断的?
问题3:当铅直高度与水平宽度的比相等时,梯子一样陡
3m
6m
D
E
F
C
2m
B
4m
A
问题4:如图,梯子AB和EF哪个更陡?你是怎样判断的?
1.5m
4m
D
E
F
C
1.3m
B
3.5m
A
看起来,好像倾斜角差不多大,他们一样陡吗?
思考:
当铅直高度与水平宽度的比不相等时,
梯子倾斜程度与铅直高度与水平宽度的比有什么关系呢?
合作探究2
6m
2m
合作探究2
问题5:(1)在这个过程中,倾斜角,铅直高度,水平宽度它们是怎么变化的呢?
问题5:你有几种方法比较梯子AB和EF哪个更陡?
当铅直高度与水平宽度的比越大,梯子越陡.
3m
2m
6m
5m
A
B
C
D
E
F
倾斜角越大,梯子越陡.
判断梯子是否更陡,有如下方法:
1.可以利用倾斜角的大小比较:倾斜角越大,梯子越陡.
2.可以利用倾斜角的对边与邻边的比值大小来判断:比值越大,梯子越陡.
要点归纳
如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度;
而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子的倾斜程度.
你同意小亮的看法吗
想一想
A
B1
C1
C2
B2
(1)Rt△AB1C1和Rt△AB2C2有什么关系
(2) 和 有什么关系
(3)如果改变点B2在梯子上的位置,这种关系还成立吗?
Rt△AB1C1 ∽Rt△AB2C2
合作探究3
A
B1
C1
C2
B2
(1)Rt△AB1C1和Rt△AB2C2有什么关系
(2) 和 有什么关系
(3)如果改变点B2在梯子上的位置,这种关系还成立吗?
Rt△AB1C1 ∽Rt△AB2C2
合作探究3
A
B1
C1
C2
B2
(1)Rt△AB1C1和Rt△AB2C2有什么关系
(2) 和 有什么关系
(3)如果改变点B2在梯子上的位置,这种关系还成立吗?
Rt△AB1C1 ∽Rt△AB2C2
合作探究3
A
B1
C1
C2
B2
(1)Rt△AB1C1和Rt△AB2C2有什么关系
(2) 和 有什么关系
(3)如果改变点B2在梯子上的位置,这种关系还成立吗?
Rt△AB1C1 ∽Rt△AB2C2
∠A不变的情况下,从任何位置测出的梯子的铅直高度与水平宽度的比值都是一定的.
合作探究3
当倾斜角确定时,它的对边与邻边的比值也随之确定的,即:这个比值只与倾斜角的大小有关,而与直角三角形的大小无关.
要点归纳
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切(tangent,音标:[ t nd nt] ),记作tanA,
即
A
B
C
∠A的对边
∠A的邻边
┌
tanA=
结论:∠A越大,tanA的值越大,梯子越陡.
引入新知
定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的,∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。对于三个大写字母或者数字表示的角则不能省略角的符号.即∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA﹥0且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序).
4)tanA不表示“tan”乘以“A ”.
例1: 下图表示两个自动扶梯,哪一个自动扶梯比较陡
解:甲梯中,
β
6m
┐
乙
8m
α
5m
┌
甲
13m
乙梯中,
∵tanβ>tanα,∴乙梯更陡.
提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.
典例精析
1.判断正误
(1)如图 (1)
( ).
(2)如图 (2)
( ).
(3)如图 (2)
( ).
(4)如图 (2)
( ).
(5)如图 (2)
( ).
×
×
×
×
A
B
C
(1)
┍
A
B
C
7m
10m
(2)
√
练一练
2. 在Rt△ABC中,∠C=90°,AC=7,BC=5,则 tan A=______,tan B =______.
练一练
互余两锐角的正切值互为倒数.
3.下图中∠ACB=90°,CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.
A
B
C
D
(1) tanA =
=
AC
( )
CD
( )
(2) tanB=
=
BC
( )
CD
( )
BC
AD
BD
AC
5.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
4.已知∠A,∠B为锐角,
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.
=
=
tanA的大小只与∠A的大小有关,而与直角三角形的边长无关
6.在等腰△ABC中, AB=AC=13, BC=10,求tanB.
提示:过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.
A
C
B
┌
D
解:如图,过点A作AD⊥BC于点D,
∴在Rt△ABD中,
易知BD=5,AD=12.
正切通常也用来描述山坡的坡度.
坡度、坡角
例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度(即tanα)就是:
坡角:坡面与水平面的夹角α称为坡角;
坡度(坡比):坡面的铅直高度与水平宽度的比称
为坡度(或坡比),即坡度等于坡角的正切.
100m
60m
┌
α
概念学习
坡度越大,坡角越大,坡面就越陡.
例2 如图所示,梯形护坡石坝的斜坡AB的坡度为1∶3,坝高BC=2米,则斜坡AB的长是( )
解析:∵∠ACB=90°,坡度为1∶3,
B
方法总结:理解坡度的概念是解决与坡度有关的计算题的关键.
∵BC=2米,∴AC=3BC=3×2=6(米).
课堂小结
正切
定义
坡度
∠A越大,tanA越大,
梯子越陡
与梯子倾斜程度的关系
作业:
课本第4页
必做:随堂练习第一题,第二题
选做:习题1.1 知识技能
同学们,愿你们学有所获!
