高中数学人教A版(2019)必修 第二册 6.4.2向量在物理中的应用举例 课件(共20张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)必修 第二册 6.4.2向量在物理中的应用举例 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 09:43:20 | ||
图片预览








文档简介
(共20张PPT)
6.4.2向量在物理中的应用举例
物理中有很多量,如力、速度等都是既有大小又有方向的量——即向量,利用向量的有关知识来研究物理中的相关问题.
温故知新
向量是怎样定义的
物理中的矢量与数学中的向量有区别吗
用数学知识解决物理问题,首先要把物理问题转化成数学问题,即将物理量之间的关系抽象成数学模型,然后再通过这个数学模型的研究解释相关物理现象.
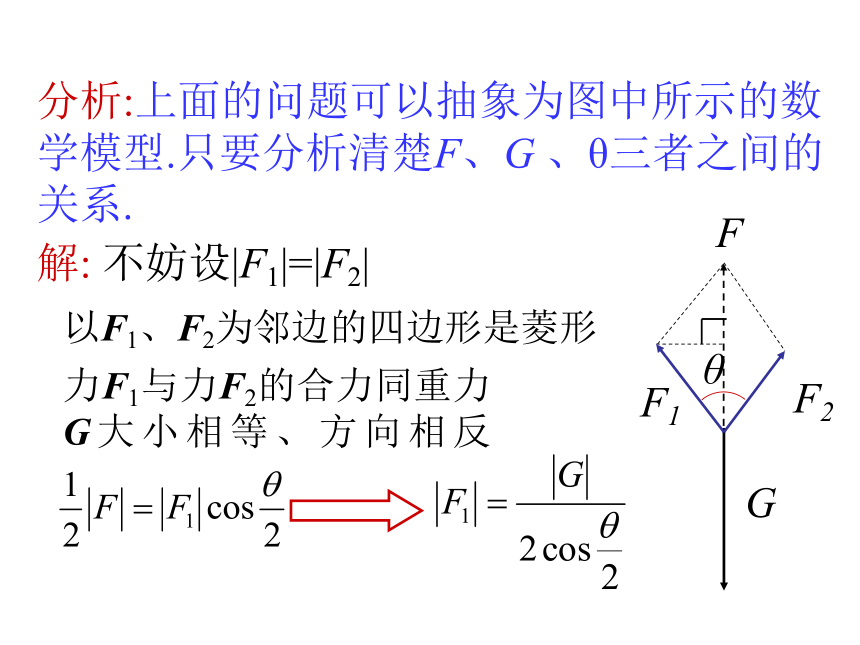
在日常生活中,你是否有这样的经验:两个人共提一个旅行包,夹角越大越费力;在单杠上做引体向上运动,两臂的夹角越小越省力.你能从数学的角度解释这种现象吗
F
G
F1
F2
θ
分析:上面的问题可以抽象为图中所示的数学模型.只要分析清楚F、G 、θ三者之间的关系.
解: 不妨设|F1|=|F2|
力F1与力F2的合力同重力G大小相等、方向相反
以F1、F2为邻边的四边形是菱形
例1 一架飞机从A地向北偏西60°的方向飞行
1 000km到达B地,然后向C地飞行.设C地恰好在A地的南偏西60°,并且A,C两地相距2 000km,求飞机从B地到C地的位移.
B
A
D
C
60o
60o
西
南
东
北
分析:
要求飞机从B地到C地的位移,需要解决两个问题:
⑴利用解三角形的知识求线段BC的长度.
⑵求BC与基线的夹角.
30°
分析:本题是向量在物理学中“力学问题”上应用的例子,可以清楚地看出向量的直接作用,根据向量数量积的几何意义,可知对物体所做的功即是表示力的向量和表示位移的向量的数量积.
例2 已知力 与水平方向的夹角为30°(斜向上),
大小为50 N,一个质量为8 kg的木块受力 的作用在
动摩擦因数μ=0.02的水平平面上运动了20 m.问力
和摩擦力 所做的功分别为多少?(g=10 m/s2)
例3:如图,一条河流的两岸平行,河的宽度d = 500m,一艘船从A处出发到河对岸。已知船的速度 =10km/h,水流的速度 = 2km/h。
问:(1)行驶航程最短时,所用的时间是多少?
(2)行驶时间最短时,所用的时间是多少?
v1
v2
分析:(1)因为两平行线之间的最短距离是它们的公垂线段。所以只有当小船的实际运动方向(即合运动方向)是垂直于河岸的方向时,小船的航程最小。
(2)小船过河的问题有一个特点,就是小船在垂直于河岸的方向上的位移是不变的,我们只要使得在垂直于河岸方向上的速度最大,小船过河所用的时间就最短,河水的速度是沿河岸方向的,这个分速度和垂直于河岸的方向没有关系,所以使小船垂直于河岸方向行驶(小船自身的速度,方向指向河对岸),小船过河所用时间才最短。
500m
A
*
把物理问题转化为数学模型为:
解(1) = =
所以
t = = 60
答:行驶的航程最短时,所用的时间是3.1min。
v
-
v1
2
v2
2
96
d
v
0.5
96
~
~
3.1(min)
(2) t = = 60 = 3 (min)
答:行驶的时间最短时,所用的时间是3min
d
v1
0.5
10
(1)
A
B
v1
v2
v
(2)
v2
v1
v
km/h
*
练习;
(1)如图所示,用两条成120 的等长的绳子悬挂一个灯具,已知灯具的重量为10N,则每根绳子的拉力是
————。
120
10N
如图,今有一艘小船位于d = 60m宽的河边P处,从这里起,在下游 =80m处河流有一处瀑布,若河水的流速方向由上游指向下游(与河岸平行),水速大小为5m/s为了使小船能安全过河,船的划速不能小于多少?当划速最小时,划速方向如何?
P
Q
瀑布
θ
Q,
60m
*
P
Q
瀑布
θ
V船
V水
V合的方向
θ
P
Q
从图上看,哪个速度(向量的模)最小?
分析:用向量来分别表示河流的水流速度、船速和它们的合速度为 、 和 ,由题意,船的实际速度为向量
其方向为临界方向 ,船只要朝着这个方向行驶,它就不会掉下瀑布,如(右)图所示:
PQ
V船
V水
V合
=
+
V船
V水
V合
解:由题意知:
其方向为临界方向 ,设 和 夹角为
θ,则最小划速为:
sinθ = =
所以:最小的船速应为:
V船
V水
V合
=
+
PQ
V水
V合
v船
=
v水
sinθ
v船
= 5 × sinθ =5 × =3(m/s)
提问:表示划船速度的向量怎样画
*
如何解决物理中与向量有关的问题:
(1)弄清物理现象中蕴含的物理量间的关系(数学模型);
(2)灵活运用数学模型研究有关物理问题;
(3)综合运用有关向量的知识,三角等和物理知识解决实际问题;
(4)用所得的结果解释物理现象。
总结:向量有关知识在物理学中应用非常广泛,它也是解释某些物理现象的重要基础知识。通过这节课的学习,我们应掌握什么内容?
*
1.一船从某河一岸驶向另一岸,船速为v1、水速为v2,若船是垂直到达对岸的,则船在河中实际航行速度的大小为( )
A.v12-v22 B.|v1|2+|v2|2
D
课堂练习
2.人骑自行车的速度为v1,风速为v2,则逆风行驶的速度大小为( )
A.v1-v2 B.|v1|+|v2|
C.|v1|-|v2| D.|v1-v2|
C
3.三个力F1、F2、F3同时作用于O点且处于平衡状态,已知F1与F3的夹角为120°,又|F1|=|F2|=20N,则|F3|= .
20N
4.已知两恒力F1=(3,4),F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0).试求:
(1)力F1,F2分别对质点所做的功;(2)F1,F2的合力对质点所做的功.
*
掌握用向量方法解决平面几何问题的三个步骤:
简述:形到向量 向量的运算 向量和数到形
6.4.2向量在物理中的应用举例
物理中有很多量,如力、速度等都是既有大小又有方向的量——即向量,利用向量的有关知识来研究物理中的相关问题.
温故知新
向量是怎样定义的
物理中的矢量与数学中的向量有区别吗
用数学知识解决物理问题,首先要把物理问题转化成数学问题,即将物理量之间的关系抽象成数学模型,然后再通过这个数学模型的研究解释相关物理现象.
在日常生活中,你是否有这样的经验:两个人共提一个旅行包,夹角越大越费力;在单杠上做引体向上运动,两臂的夹角越小越省力.你能从数学的角度解释这种现象吗
F
G
F1
F2
θ
分析:上面的问题可以抽象为图中所示的数学模型.只要分析清楚F、G 、θ三者之间的关系.
解: 不妨设|F1|=|F2|
力F1与力F2的合力同重力G大小相等、方向相反
以F1、F2为邻边的四边形是菱形
例1 一架飞机从A地向北偏西60°的方向飞行
1 000km到达B地,然后向C地飞行.设C地恰好在A地的南偏西60°,并且A,C两地相距2 000km,求飞机从B地到C地的位移.
B
A
D
C
60o
60o
西
南
东
北
分析:
要求飞机从B地到C地的位移,需要解决两个问题:
⑴利用解三角形的知识求线段BC的长度.
⑵求BC与基线的夹角.
30°
分析:本题是向量在物理学中“力学问题”上应用的例子,可以清楚地看出向量的直接作用,根据向量数量积的几何意义,可知对物体所做的功即是表示力的向量和表示位移的向量的数量积.
例2 已知力 与水平方向的夹角为30°(斜向上),
大小为50 N,一个质量为8 kg的木块受力 的作用在
动摩擦因数μ=0.02的水平平面上运动了20 m.问力
和摩擦力 所做的功分别为多少?(g=10 m/s2)
例3:如图,一条河流的两岸平行,河的宽度d = 500m,一艘船从A处出发到河对岸。已知船的速度 =10km/h,水流的速度 = 2km/h。
问:(1)行驶航程最短时,所用的时间是多少?
(2)行驶时间最短时,所用的时间是多少?
v1
v2
分析:(1)因为两平行线之间的最短距离是它们的公垂线段。所以只有当小船的实际运动方向(即合运动方向)是垂直于河岸的方向时,小船的航程最小。
(2)小船过河的问题有一个特点,就是小船在垂直于河岸的方向上的位移是不变的,我们只要使得在垂直于河岸方向上的速度最大,小船过河所用的时间就最短,河水的速度是沿河岸方向的,这个分速度和垂直于河岸的方向没有关系,所以使小船垂直于河岸方向行驶(小船自身的速度,方向指向河对岸),小船过河所用时间才最短。
500m
A
*
把物理问题转化为数学模型为:
解(1) = =
所以
t = = 60
答:行驶的航程最短时,所用的时间是3.1min。
v
-
v1
2
v2
2
96
d
v
0.5
96
~
~
3.1(min)
(2) t = = 60 = 3 (min)
答:行驶的时间最短时,所用的时间是3min
d
v1
0.5
10
(1)
A
B
v1
v2
v
(2)
v2
v1
v
km/h
*
练习;
(1)如图所示,用两条成120 的等长的绳子悬挂一个灯具,已知灯具的重量为10N,则每根绳子的拉力是
————。
120
10N
如图,今有一艘小船位于d = 60m宽的河边P处,从这里起,在下游 =80m处河流有一处瀑布,若河水的流速方向由上游指向下游(与河岸平行),水速大小为5m/s为了使小船能安全过河,船的划速不能小于多少?当划速最小时,划速方向如何?
P
Q
瀑布
θ
Q,
60m
*
P
Q
瀑布
θ
V船
V水
V合的方向
θ
P
Q
从图上看,哪个速度(向量的模)最小?
分析:用向量来分别表示河流的水流速度、船速和它们的合速度为 、 和 ,由题意,船的实际速度为向量
其方向为临界方向 ,船只要朝着这个方向行驶,它就不会掉下瀑布,如(右)图所示:
PQ
V船
V水
V合
=
+
V船
V水
V合
解:由题意知:
其方向为临界方向 ,设 和 夹角为
θ,则最小划速为:
sinθ = =
所以:最小的船速应为:
V船
V水
V合
=
+
PQ
V水
V合
v船
=
v水
sinθ
v船
= 5 × sinθ =5 × =3(m/s)
提问:表示划船速度的向量怎样画
*
如何解决物理中与向量有关的问题:
(1)弄清物理现象中蕴含的物理量间的关系(数学模型);
(2)灵活运用数学模型研究有关物理问题;
(3)综合运用有关向量的知识,三角等和物理知识解决实际问题;
(4)用所得的结果解释物理现象。
总结:向量有关知识在物理学中应用非常广泛,它也是解释某些物理现象的重要基础知识。通过这节课的学习,我们应掌握什么内容?
*
1.一船从某河一岸驶向另一岸,船速为v1、水速为v2,若船是垂直到达对岸的,则船在河中实际航行速度的大小为( )
A.v12-v22 B.|v1|2+|v2|2
D
课堂练习
2.人骑自行车的速度为v1,风速为v2,则逆风行驶的速度大小为( )
A.v1-v2 B.|v1|+|v2|
C.|v1|-|v2| D.|v1-v2|
C
3.三个力F1、F2、F3同时作用于O点且处于平衡状态,已知F1与F3的夹角为120°,又|F1|=|F2|=20N,则|F3|= .
20N
4.已知两恒力F1=(3,4),F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0).试求:
(1)力F1,F2分别对质点所做的功;(2)F1,F2的合力对质点所做的功.
*
掌握用向量方法解决平面几何问题的三个步骤:
简述:形到向量 向量的运算 向量和数到形
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
