6.4.3.3余弦定理、正弦定理应用举例课件(56张ppt)
文档属性
| 名称 | 6.4.3.3余弦定理、正弦定理应用举例课件(56张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 17:38:44 | ||
图片预览







文档简介
(共56张PPT)
6.4.3.3余弦定理、正弦定理应用举例
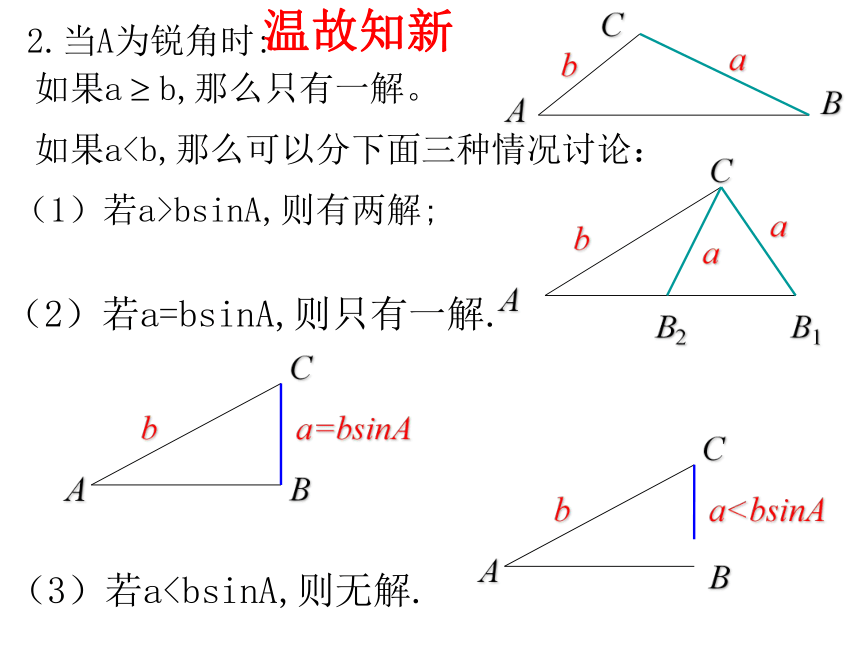
温故知新
1.正弦定理
正弦定理的变形:
2.余弦定理
余弦定理的变形:
温故知新
3.三角形面积公式
温故知新
4.三角形中的常见结论
(2)在三角形中大边对大角,大角对大边.
(3)任意两边之和大于第三边,任意两边之差小于第三边
(4)有关三角形内角的三角函数式
温故知新
(5) 中,A、B、C成等差数列的充要条件
是B=60
温故知新
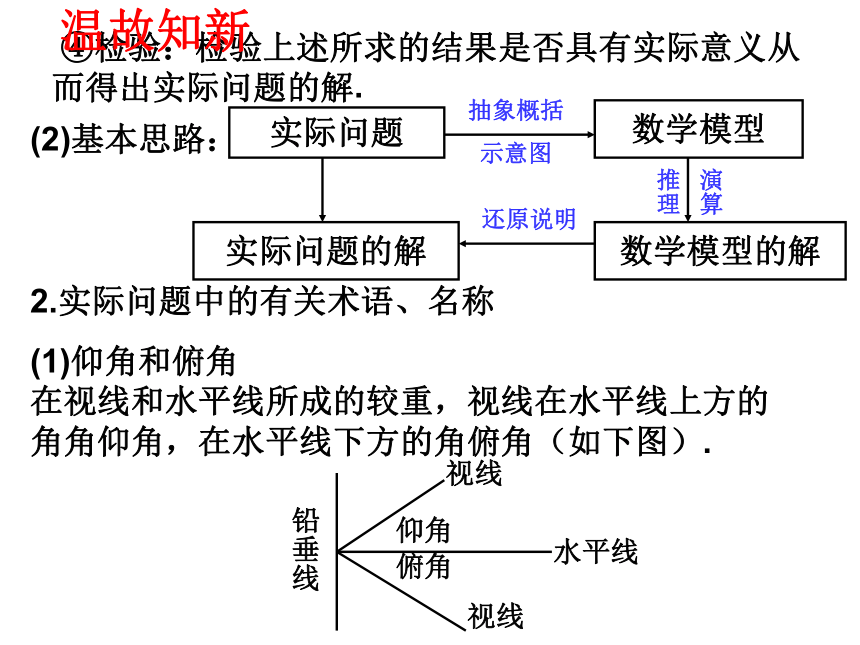
(2)基本思路:
实际问题
数学模型
数学模型的解
实际问题的解
抽象概括
示意图
演算
推理
还原说明
2.实际问题中的有关术语、名称
(1)仰角和俯角 在视线和水平线所成的较重,视线在水平线上方的角角仰角,在水平线下方的角俯角(如下图).
铅垂线
视线
视线
水平线
仰角
俯角
④检验:检验上述所求的结果是否具有实际意义从而得出实际问题的解.
温故知新
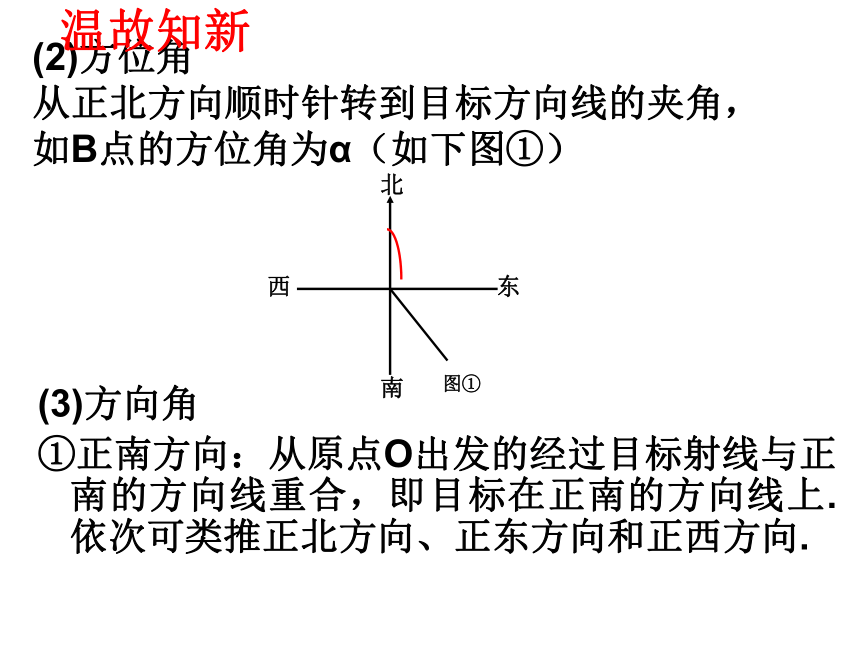
(2)方位角
从正北方向顺时针转到目标方向线的夹角,如B点的方位角为α(如下图①)
(3)方向角
①正南方向:从原点O出发的经过目标射线与正南的方向线重合,即目标在正南的方向线上.依次可类推正北方向、正东方向和正西方向.
西 东
北 南
图①
温故知新
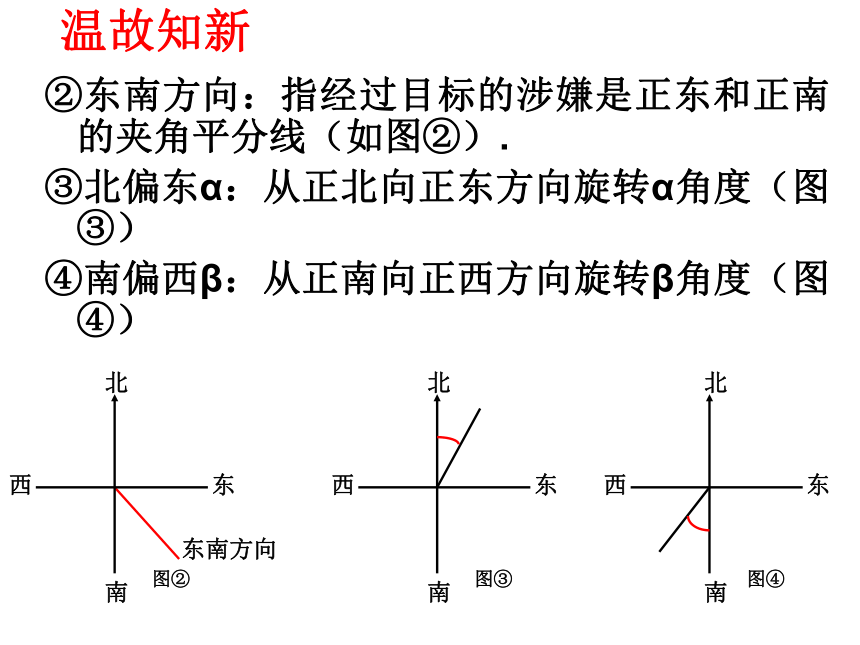
②东南方向:指经过目标的涉嫌是正东和正南的夹角平分线(如图②).
③北偏东α:从正北向正东方向旋转α角度(图③)
④南偏西β:从正南向正西方向旋转β角度(图④)
西 东
北 南
图④
东南方向
西 东
北 南
图②
西 东
北 南
图③
温故知新
A
A
B
B
C
C
a
a
b
b
温故知新
A
B
C
a
b
A
B1
B2
C
a
a
b
A
B
C
b
a=bsinA
A
B
C
b
a温故知新
方法二:画圆法
温故知新
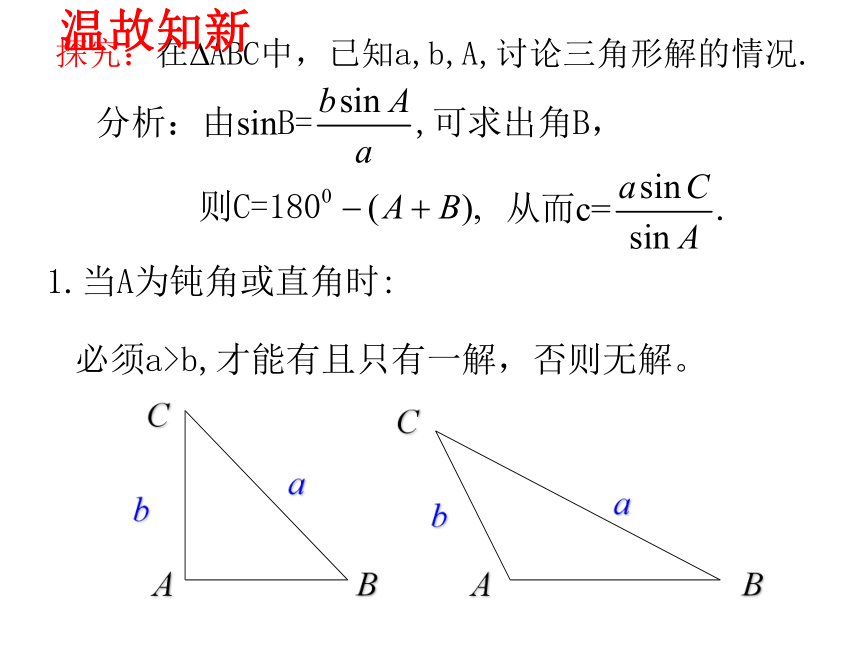
若A为锐角时:
若A为直角或钝角时:
温故知新
题型一 计算三角形的面积
【例1】
如图,在△ABC中,已知,B=45°,D是BC边上的一点,AD=5,AC=7,DC=3,求AB的长.
【例2】
题型二 计算线段的长度
已知AB⊥BD,AC⊥CD,AC=1,AB=2,∠BAC=120°,求BD的长.
【例3】
(1)求角C的大小;(2)求sin A+sin B的最大值..
【题后反思】 此类问题常以三角形为载体,以正、余弦定理和三角函数公式为工具来综合考查,因此要掌握正、余弦定理,掌握三角函数的公式和性质.
【训练3】
A
C
B
51o
55m
75o
例1.设A、B两点在河的两岸,要测量两点之间的距离。
测量者在A的同测,在所在的河岸边选定一点C,测出AC的距离是55cm,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)
分析:已知两角一边,可以用正弦定理解三角形
解:根据正弦定理,得
答:A,B两点间的距离为65.7米。
A
B
C
D
A
B
C
D
α
β
γ
δ
a
解:如图,测量者可以在河岸边选定两点C、D,设CD=a,∠BCA=α,∠ACD=β,∠CDB=γ,
∠ADB=δ
分析:用例1的方法,可以计算出河的这一岸的一点C到对岸两点的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离。
解:测量者可以在河岸边选定两点C、D,测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在 ADC和 BDC中,应用正弦定理得
计算出AC和BC后,再在 ABC中,应用余弦定理计算出AB两点间的距离
变式训练:若在河岸选取相距40米的C、D两点,测得 BCA= , ACD= , CDB= ,BDA=
求A、B两点间距离 .
练习1.一艘船以32.2n mile / hr的速度向正北航行。在A处看灯塔C在船的北偏东20o的方向,30min后航行到B处,在B处看灯塔在船的北偏东65o的方向,已知距离此灯塔6.5n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
C
变式练习:两灯塔A、B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东30o,灯塔B在观察站C南偏东60o,则A、B之间的距离为多少?
练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m).
最大角度
最大角度
最大角度
最大角度
C
A
B
练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m).
最大角度
最大角度
最大角度
最大角度
已知△ABC中AB=1.95m,AC=1.40m,
夹角∠CAB=66°20′,求BC.
解:由余弦定理,得
答:顶杆BC约长1.89m。
C
A
B
测量垂直高度
1、底部可以到达的
测量出角C和BC的长度,解直角三角形即可求出AB的长。
图中给出了怎样的一个
几何图形?已知什么,
求什么?
想一想
B
E
A
G
H
D
C
2、底部不能到达的
例3 AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法
分析:由于建筑物的底部B是不可到达的,所以不能直接测量出建筑物的高。由解直角三角形的知识,只要能测出一点C到建筑物的顶部A的距离CA,并测出由点C观察A的仰角,就可以计算出建筑物的高。所以应该设法借助解三角形的知识测出CA的长。
B
E
A
G
H
D
C
解:选择一条水平基线HG,使H,G,B三点在同一条直线上。由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.那么,在 ACD中,根据正弦定理可得
例3. AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法
B
E
A
G
H
D
C
分析:根据已知条件,应该设法计算出AB或AC的长
A
B
C
D
a
b
CD=BD-BC≈177-27.3=150(m)
答:山的高度约为150米。
解:在⊿ABC中,∠BCA= 90° +β, ∠ABC= 90° -α, ∠BAC=α-β, ∠BAD=α.根据正弦定理,
A
B
C
D
a
b
例3:如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北150的方向上,行驶5km后到达B处,测得此山顶在西偏北250的方向上,仰角为80,求此山的高度CD
例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.
解:在⊿ABC中,∠A=15°,
∠C= 25° 15°=10°.
根据正弦定理,
CD=BC×tan∠DBC≈BC×tan8°≈1047(m)
答:山的高度约为1047米。
变式:某人在M汽车站的北偏西200的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶。公路的走向是M站的北偏东400。开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米。问汽车还需行驶多远,才能到达M汽车站?
例6 一艘海轮从A出发,沿北偏东75°的方向航行67.5n mile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离(角度精确到0.1°,距离精确到0.01n mile)
解:在 △ABC中,∠ABC=180°-75°+32°=137°,根据余弦定理,
1 如图,两点C,D与烟囱底部在同一水平直线上,在点C1 ,D1,利用高为1.5m的测角仪器,测得烟囱的仰角分别是 =45°和 =60°, C、D间的距离是12m. 计算烟囱的高AB(结果精确到0.01m).
D
C
B
A
A1
C1
D1
课堂训练
分析:如图所示,因为AB=AA1+A1B,又已知AA1=1.5m,所以只要求出A1B即可.
3.我军有A、B两个小岛相距10海里,敌军在C岛,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,为提高炮弹命中率,须计算B岛和C岛
间的距离,请你算算看.
A
C
B
10海里
60°
75°
4.如图,一艘船以32海里/时的速度向正北航行,在A处看灯塔S在船的北偏东20°, 30分钟后航行到B处,在B处看灯塔S在船的北偏东65°方向上,求灯塔S和B处的距离.(保留到0.1)
解:AB=16,由正弦定理知:
可求得BS≈7.7海里.
答:灯塔S和B处的距离为7.7海里.
A
B
S
16
?
5 一次机器人足球比赛中,甲队1号机器由点A开始作匀速直线运动,到达B点时,发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动.如图,已知
若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球
A
B
D
45O
分析 机器人最快截住足球的地方正是机器人与足球同时到达的地方,设为C点.利用速度建立AC与BC之间的关系,再利用余弦定理便可建立方程解决问题.
解.设机器人最快可在C处截住足球,点C在线段AD上.设BC=x dm,由题意,CD=2x dm.
A
B
D
45O
C
AC=AD-CD=(17-2x) dm.
在△BCD中,由余弦定理,得.
即
解得
所以
(不合题意,舍去)
答 该机器人最快可在线段AD上离点A7dm的点C处截住足球.
6如图,已知⊙O的半径是1,点C在直径AB的延长线上,BC=1,点P是⊙O上半圆上的一个动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.
(1)若∠POB=θ,试将四边形OPDC的面积y表示成θ的函数;
(2)求四边形OPDC面积的最大值.
A
O
B
D
C
P
分析 四边形OPDC可以分成△OPC与△PCD.S△OPC可用
表示;而求△PCD的面积的关键在于求出边长PC,在△OPC中利用余弦定理即可求出;面积最值,可通过函数解决.
解.(1)在△POC中,由余弦定理,得.
所以
(2)当
时,
6.4.3.3余弦定理、正弦定理应用举例
温故知新
1.正弦定理
正弦定理的变形:
2.余弦定理
余弦定理的变形:
温故知新
3.三角形面积公式
温故知新
4.三角形中的常见结论
(2)在三角形中大边对大角,大角对大边.
(3)任意两边之和大于第三边,任意两边之差小于第三边
(4)有关三角形内角的三角函数式
温故知新
(5) 中,A、B、C成等差数列的充要条件
是B=60
温故知新
(2)基本思路:
实际问题
数学模型
数学模型的解
实际问题的解
抽象概括
示意图
演算
推理
还原说明
2.实际问题中的有关术语、名称
(1)仰角和俯角 在视线和水平线所成的较重,视线在水平线上方的角角仰角,在水平线下方的角俯角(如下图).
铅垂线
视线
视线
水平线
仰角
俯角
④检验:检验上述所求的结果是否具有实际意义从而得出实际问题的解.
温故知新
(2)方位角
从正北方向顺时针转到目标方向线的夹角,如B点的方位角为α(如下图①)
(3)方向角
①正南方向:从原点O出发的经过目标射线与正南的方向线重合,即目标在正南的方向线上.依次可类推正北方向、正东方向和正西方向.
西 东
北 南
图①
温故知新
②东南方向:指经过目标的涉嫌是正东和正南的夹角平分线(如图②).
③北偏东α:从正北向正东方向旋转α角度(图③)
④南偏西β:从正南向正西方向旋转β角度(图④)
西 东
北 南
图④
东南方向
西 东
北 南
图②
西 东
北 南
图③
温故知新
A
A
B
B
C
C
a
a
b
b
温故知新
A
B
C
a
b
A
B1
B2
C
a
a
b
A
B
C
b
a=bsinA
A
B
C
b
a
方法二:画圆法
温故知新
若A为锐角时:
若A为直角或钝角时:
温故知新
题型一 计算三角形的面积
【例1】
如图,在△ABC中,已知,B=45°,D是BC边上的一点,AD=5,AC=7,DC=3,求AB的长.
【例2】
题型二 计算线段的长度
已知AB⊥BD,AC⊥CD,AC=1,AB=2,∠BAC=120°,求BD的长.
【例3】
(1)求角C的大小;(2)求sin A+sin B的最大值..
【题后反思】 此类问题常以三角形为载体,以正、余弦定理和三角函数公式为工具来综合考查,因此要掌握正、余弦定理,掌握三角函数的公式和性质.
【训练3】
A
C
B
51o
55m
75o
例1.设A、B两点在河的两岸,要测量两点之间的距离。
测量者在A的同测,在所在的河岸边选定一点C,测出AC的距离是55cm,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)
分析:已知两角一边,可以用正弦定理解三角形
解:根据正弦定理,得
答:A,B两点间的距离为65.7米。
A
B
C
D
A
B
C
D
α
β
γ
δ
a
解:如图,测量者可以在河岸边选定两点C、D,设CD=a,∠BCA=α,∠ACD=β,∠CDB=γ,
∠ADB=δ
分析:用例1的方法,可以计算出河的这一岸的一点C到对岸两点的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离。
解:测量者可以在河岸边选定两点C、D,测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在 ADC和 BDC中,应用正弦定理得
计算出AC和BC后,再在 ABC中,应用余弦定理计算出AB两点间的距离
变式训练:若在河岸选取相距40米的C、D两点,测得 BCA= , ACD= , CDB= ,BDA=
求A、B两点间距离 .
练习1.一艘船以32.2n mile / hr的速度向正北航行。在A处看灯塔C在船的北偏东20o的方向,30min后航行到B处,在B处看灯塔在船的北偏东65o的方向,已知距离此灯塔6.5n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
C
变式练习:两灯塔A、B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东30o,灯塔B在观察站C南偏东60o,则A、B之间的距离为多少?
练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m).
最大角度
最大角度
最大角度
最大角度
C
A
B
练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m).
最大角度
最大角度
最大角度
最大角度
已知△ABC中AB=1.95m,AC=1.40m,
夹角∠CAB=66°20′,求BC.
解:由余弦定理,得
答:顶杆BC约长1.89m。
C
A
B
测量垂直高度
1、底部可以到达的
测量出角C和BC的长度,解直角三角形即可求出AB的长。
图中给出了怎样的一个
几何图形?已知什么,
求什么?
想一想
B
E
A
G
H
D
C
2、底部不能到达的
例3 AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法
分析:由于建筑物的底部B是不可到达的,所以不能直接测量出建筑物的高。由解直角三角形的知识,只要能测出一点C到建筑物的顶部A的距离CA,并测出由点C观察A的仰角,就可以计算出建筑物的高。所以应该设法借助解三角形的知识测出CA的长。
B
E
A
G
H
D
C
解:选择一条水平基线HG,使H,G,B三点在同一条直线上。由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.那么,在 ACD中,根据正弦定理可得
例3. AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法
B
E
A
G
H
D
C
分析:根据已知条件,应该设法计算出AB或AC的长
A
B
C
D
a
b
CD=BD-BC≈177-27.3=150(m)
答:山的高度约为150米。
解:在⊿ABC中,∠BCA= 90° +β, ∠ABC= 90° -α, ∠BAC=α-β, ∠BAD=α.根据正弦定理,
A
B
C
D
a
b
例3:如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北150的方向上,行驶5km后到达B处,测得此山顶在西偏北250的方向上,仰角为80,求此山的高度CD
例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.
解:在⊿ABC中,∠A=15°,
∠C= 25° 15°=10°.
根据正弦定理,
CD=BC×tan∠DBC≈BC×tan8°≈1047(m)
答:山的高度约为1047米。
变式:某人在M汽车站的北偏西200的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶。公路的走向是M站的北偏东400。开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米。问汽车还需行驶多远,才能到达M汽车站?
例6 一艘海轮从A出发,沿北偏东75°的方向航行67.5n mile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离(角度精确到0.1°,距离精确到0.01n mile)
解:在 △ABC中,∠ABC=180°-75°+32°=137°,根据余弦定理,
1 如图,两点C,D与烟囱底部在同一水平直线上,在点C1 ,D1,利用高为1.5m的测角仪器,测得烟囱的仰角分别是 =45°和 =60°, C、D间的距离是12m. 计算烟囱的高AB(结果精确到0.01m).
D
C
B
A
A1
C1
D1
课堂训练
分析:如图所示,因为AB=AA1+A1B,又已知AA1=1.5m,所以只要求出A1B即可.
3.我军有A、B两个小岛相距10海里,敌军在C岛,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,为提高炮弹命中率,须计算B岛和C岛
间的距离,请你算算看.
A
C
B
10海里
60°
75°
4.如图,一艘船以32海里/时的速度向正北航行,在A处看灯塔S在船的北偏东20°, 30分钟后航行到B处,在B处看灯塔S在船的北偏东65°方向上,求灯塔S和B处的距离.(保留到0.1)
解:AB=16,由正弦定理知:
可求得BS≈7.7海里.
答:灯塔S和B处的距离为7.7海里.
A
B
S
16
?
5 一次机器人足球比赛中,甲队1号机器由点A开始作匀速直线运动,到达B点时,发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动.如图,已知
若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球
A
B
D
45O
分析 机器人最快截住足球的地方正是机器人与足球同时到达的地方,设为C点.利用速度建立AC与BC之间的关系,再利用余弦定理便可建立方程解决问题.
解.设机器人最快可在C处截住足球,点C在线段AD上.设BC=x dm,由题意,CD=2x dm.
A
B
D
45O
C
AC=AD-CD=(17-2x) dm.
在△BCD中,由余弦定理,得.
即
解得
所以
(不合题意,舍去)
答 该机器人最快可在线段AD上离点A7dm的点C处截住足球.
6如图,已知⊙O的半径是1,点C在直径AB的延长线上,BC=1,点P是⊙O上半圆上的一个动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.
(1)若∠POB=θ,试将四边形OPDC的面积y表示成θ的函数;
(2)求四边形OPDC面积的最大值.
A
O
B
D
C
P
分析 四边形OPDC可以分成△OPC与△PCD.S△OPC可用
表示;而求△PCD的面积的关键在于求出边长PC,在△OPC中利用余弦定理即可求出;面积最值,可通过函数解决.
解.(1)在△POC中,由余弦定理,得.
所以
(2)当
时,
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
