1.3空间几何体的表面积与体积同步课时作业-2021-2022学年高一下学期数学人教A版必修2(word含解析)
文档属性
| 名称 | 1.3空间几何体的表面积与体积同步课时作业-2021-2022学年高一下学期数学人教A版必修2(word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 524.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 10:04:11 | ||
图片预览


文档简介
1.3 空间几何体的表面积与体积-2021-2022学年高一数学人教A版必修2同步课时作业
1.长方体中,,,,P为该正方体侧面内(含边界)的动点,且满足.则四棱锥体积的取值范围是( )
A. B. C. D.
2.已知圆锥的顶点为P,母线PA,PB所成角的余弦值为,PA与圆锥底面所成角为.若的面积为,则该圆锥的体积为( )
A. B. C. D.
3.《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥为鳖臑,平面ABC,,,三棱锥的四个顶点都在球O的球面上,则球O的表面积为( )
A.12π B.20π C.24π D.32π
4.在圆柱内有一个球O,球O分别与圆柱的上、下底面及母线均有且只有一个公共点.若,则圆柱的表面积为( )
A.4π B.5π C.6π D.7π
5.已知球O的半径为2,三棱锥四个顶点都在球O上,球心O在平面内,是正三角形,则三棱锥的最大体积为( )
A. B. C. D.3
6.如果一个长方体的长、宽、高分别是6,5,3,则它的体积为( )
A.15 B.18 C.30 D.90
7.在《九章算术·商功》中将正四面形棱台体(棱台的上、下底面均为正方形)称为方亭.在方亭中,,四个侧面均为全等的等腰梯形且面积之和为,则该方亭的体积为( )
A. B. C. D.
8.一个圆柱的侧面展开图是一个面积为的正方形,则这个圆柱的体积为( )
A. B. C. D.
9.在长方体中,,,,M,N分别在线段和AC上,,则三棱锥的体积最小值为( )
A.4 B. C. D.
10.已知球O,过其球面上A,B,C三点作截面,若点O到该截面的距离是球半径的一半,且,,则球O的表面积为( )
A. B. C. D.
11.已知四棱台,中,上、下底面都是正方形,下底面棱长为2,其余各棱长均为1,则该四棱台的外接球的表面积为__________.
12.三棱锥中,,,点D是侧棱PB的中点,且,则三棱锥的外接球O的表面积___________.
13.在平面四边形PACB中,已知,,,.沿对角线AB折起得到四面体,当PA与平面ABC所成的角最大时,该四面体的外接球的半径为_________.
14.已知四棱锥中,,,,,,平面ABCD,.
(1)设平面平面,求证:;
(2)若E是PA的中点,求四面体PBEC的体积.
答案以及解析
1.答案:A
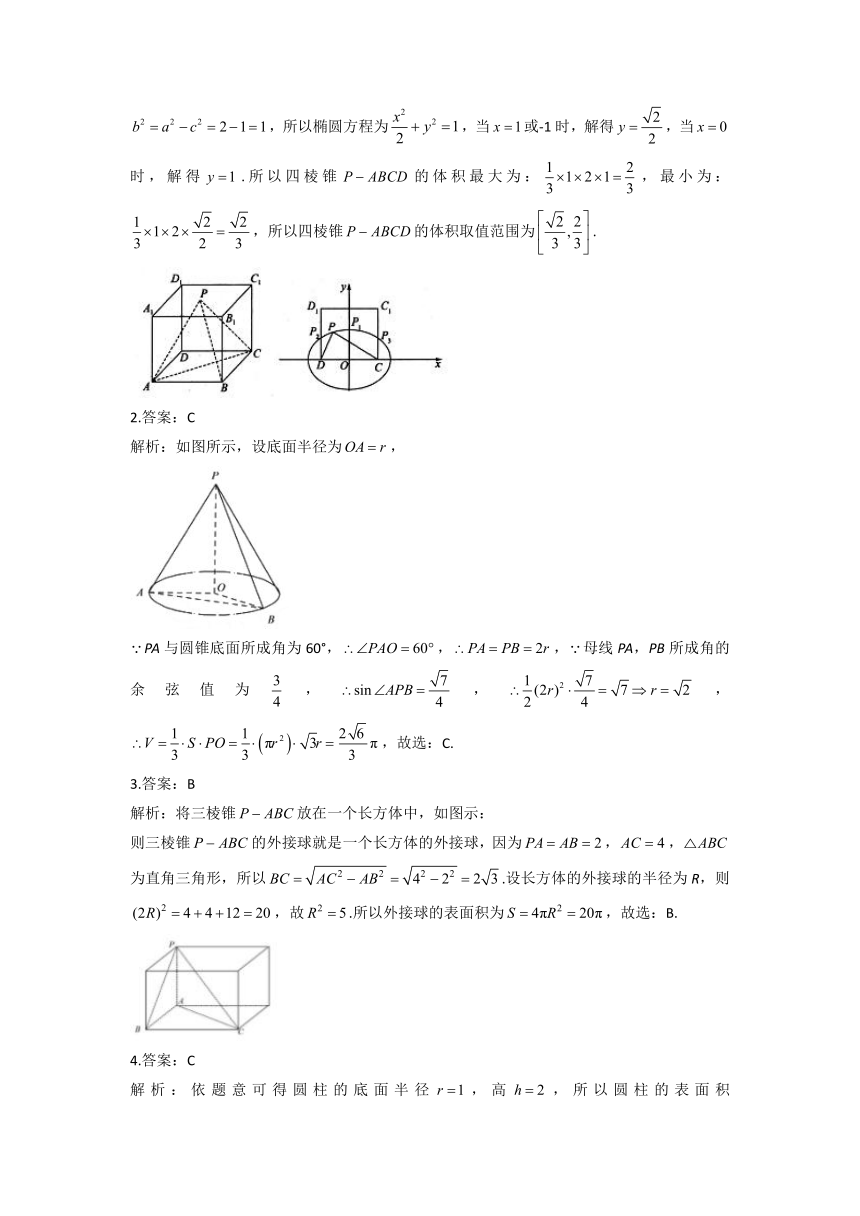
解析:,由椭圆性质可知,点P在面中运动的轨迹为椭圆的一段弧,在平面直角坐标系中画出平面和点P轨迹如下图所示,因为四棱锥底面积不变,所以当点P运动到位置时,体积最大,当点P运动到或位置时,体积最小,设椭圆方程为,因为中,所以,解得,因为,所以,所以,所以椭圆方程为,当或-1时,解得,当时,解得.所以四棱锥的体积最大为:,最小为:,所以四棱锥的体积取值范围为.
2.答案:C
解析:如图所示,设底面半径为,
PA与圆锥底面所成角为60°,,,母线PA,PB所成角的余弦值为,,,,故选:C.
3.答案:B
解析:将三棱锥放在一个长方体中,如图示:
则三棱锥的外接球就是一个长方体的外接球,因为,,为直角三角形,所以.设长方体的外接球的半径为R,则,故.所以外接球的表面积为,故选:B.
4.答案:C
解析:依题意可得圆柱的底面半径,高,所以圆柱的表面积.故选:C.
5.答案:B
解析:由于球O的半径为2,是正三角形,所以,,
所以当平面ABC时,三棱锥的体积最大.
三棱锥的最大体积为.
6.答案:D
解析:长方形体积=
7.答案:B
解析:如图,过点作,垂足为E,由四个侧面的面积之和为可知,侧面的面积为,所以,则.由题意得,在中,.连接AC,,过点作,垂足为F,易知四边形为等腰梯形,且,,则,所以,所以该方亭的体积,故选B.
8.答案:D
解析:设圆柱的底面半径为r,则底面圆的周长为,根据圆柱的侧面展开图是面积为的正方形知,,,所以这个圆柱的体积为.故选:D.
9.答案:A
解析:如图,平面就是平面,因此点D到平面的距离为定值.
由题意易知四边形是正方形,由对称性知当M(或N)与A重合时,到直线MN的距离最小,最小值为5,此时,所以.故选A.
10.答案:A
解析:如图,
设球O的半径为R,是的外心,外接圆的半径为r,
则平面ABC,在中,,,则,
由正弦定理可得,即,
在中,有,得,
球O的表面积为.
11.答案:
解析:沿四棱台的相对侧棱,,作截面大圆,如图所示.
过球心O作AC的垂线交AC于点E,交于点,连接OA,,设球的半径为R,由题知,,,所以,,从而,解得,所以该四棱台的外接球的表面积为.
12.答案:
解析:依题意,由,,得.连接AD,由点D是PB的中点且,得,又,,可知,又,平面PAB,平面PAB,所以平面PAB.
以为底面,AC为侧棱补成一个直三棱柱,则球O是该三棱柱的外接球,球心O到底面的距离.由正弦定理得的外接圆半径,所以球O的半径,故球O的表面积.
13.答案:
解析:当PA与平面ABC所成的角最大时,最大角为,此时平面平面ABC.
在中,由余弦定理可得,又,为直角三角形,,平面PAB.
如图,设四面体的外接球的球心为O,截面ABC对应圆的圆心为,截面PAB对应圆的圆心为H,E为AB的中点,则球心O到平面PAB的距离为.设的外接圆半径为r,由正弦定理可得,则.设四面体的外接球半径为R,连接OA,AH在中,,解得.
14.答案:(1)见解析
(2)
解析:(1)证明:因为,平面PAB,平面PAB,
所以平面PAB.
因为平面PCD,平面平面,
所以.
(2)解:,
平面PAB,所以C,D两点到平面PAB的距离相等.
由条件易得平面PAB且
.
1.长方体中,,,,P为该正方体侧面内(含边界)的动点,且满足.则四棱锥体积的取值范围是( )
A. B. C. D.
2.已知圆锥的顶点为P,母线PA,PB所成角的余弦值为,PA与圆锥底面所成角为.若的面积为,则该圆锥的体积为( )
A. B. C. D.
3.《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥为鳖臑,平面ABC,,,三棱锥的四个顶点都在球O的球面上,则球O的表面积为( )
A.12π B.20π C.24π D.32π
4.在圆柱内有一个球O,球O分别与圆柱的上、下底面及母线均有且只有一个公共点.若,则圆柱的表面积为( )
A.4π B.5π C.6π D.7π
5.已知球O的半径为2,三棱锥四个顶点都在球O上,球心O在平面内,是正三角形,则三棱锥的最大体积为( )
A. B. C. D.3
6.如果一个长方体的长、宽、高分别是6,5,3,则它的体积为( )
A.15 B.18 C.30 D.90
7.在《九章算术·商功》中将正四面形棱台体(棱台的上、下底面均为正方形)称为方亭.在方亭中,,四个侧面均为全等的等腰梯形且面积之和为,则该方亭的体积为( )
A. B. C. D.
8.一个圆柱的侧面展开图是一个面积为的正方形,则这个圆柱的体积为( )
A. B. C. D.
9.在长方体中,,,,M,N分别在线段和AC上,,则三棱锥的体积最小值为( )
A.4 B. C. D.
10.已知球O,过其球面上A,B,C三点作截面,若点O到该截面的距离是球半径的一半,且,,则球O的表面积为( )
A. B. C. D.
11.已知四棱台,中,上、下底面都是正方形,下底面棱长为2,其余各棱长均为1,则该四棱台的外接球的表面积为__________.
12.三棱锥中,,,点D是侧棱PB的中点,且,则三棱锥的外接球O的表面积___________.
13.在平面四边形PACB中,已知,,,.沿对角线AB折起得到四面体,当PA与平面ABC所成的角最大时,该四面体的外接球的半径为_________.
14.已知四棱锥中,,,,,,平面ABCD,.
(1)设平面平面,求证:;
(2)若E是PA的中点,求四面体PBEC的体积.
答案以及解析
1.答案:A
解析:,由椭圆性质可知,点P在面中运动的轨迹为椭圆的一段弧,在平面直角坐标系中画出平面和点P轨迹如下图所示,因为四棱锥底面积不变,所以当点P运动到位置时,体积最大,当点P运动到或位置时,体积最小,设椭圆方程为,因为中,所以,解得,因为,所以,所以,所以椭圆方程为,当或-1时,解得,当时,解得.所以四棱锥的体积最大为:,最小为:,所以四棱锥的体积取值范围为.
2.答案:C
解析:如图所示,设底面半径为,
PA与圆锥底面所成角为60°,,,母线PA,PB所成角的余弦值为,,,,故选:C.
3.答案:B
解析:将三棱锥放在一个长方体中,如图示:
则三棱锥的外接球就是一个长方体的外接球,因为,,为直角三角形,所以.设长方体的外接球的半径为R,则,故.所以外接球的表面积为,故选:B.
4.答案:C
解析:依题意可得圆柱的底面半径,高,所以圆柱的表面积.故选:C.
5.答案:B
解析:由于球O的半径为2,是正三角形,所以,,
所以当平面ABC时,三棱锥的体积最大.
三棱锥的最大体积为.
6.答案:D
解析:长方形体积=
7.答案:B
解析:如图,过点作,垂足为E,由四个侧面的面积之和为可知,侧面的面积为,所以,则.由题意得,在中,.连接AC,,过点作,垂足为F,易知四边形为等腰梯形,且,,则,所以,所以该方亭的体积,故选B.
8.答案:D
解析:设圆柱的底面半径为r,则底面圆的周长为,根据圆柱的侧面展开图是面积为的正方形知,,,所以这个圆柱的体积为.故选:D.
9.答案:A
解析:如图,平面就是平面,因此点D到平面的距离为定值.
由题意易知四边形是正方形,由对称性知当M(或N)与A重合时,到直线MN的距离最小,最小值为5,此时,所以.故选A.
10.答案:A
解析:如图,
设球O的半径为R,是的外心,外接圆的半径为r,
则平面ABC,在中,,,则,
由正弦定理可得,即,
在中,有,得,
球O的表面积为.
11.答案:
解析:沿四棱台的相对侧棱,,作截面大圆,如图所示.
过球心O作AC的垂线交AC于点E,交于点,连接OA,,设球的半径为R,由题知,,,所以,,从而,解得,所以该四棱台的外接球的表面积为.
12.答案:
解析:依题意,由,,得.连接AD,由点D是PB的中点且,得,又,,可知,又,平面PAB,平面PAB,所以平面PAB.
以为底面,AC为侧棱补成一个直三棱柱,则球O是该三棱柱的外接球,球心O到底面的距离.由正弦定理得的外接圆半径,所以球O的半径,故球O的表面积.
13.答案:
解析:当PA与平面ABC所成的角最大时,最大角为,此时平面平面ABC.
在中,由余弦定理可得,又,为直角三角形,,平面PAB.
如图,设四面体的外接球的球心为O,截面ABC对应圆的圆心为,截面PAB对应圆的圆心为H,E为AB的中点,则球心O到平面PAB的距离为.设的外接圆半径为r,由正弦定理可得,则.设四面体的外接球半径为R,连接OA,AH在中,,解得.
14.答案:(1)见解析
(2)
解析:(1)证明:因为,平面PAB,平面PAB,
所以平面PAB.
因为平面PCD,平面平面,
所以.
(2)解:,
平面PAB,所以C,D两点到平面PAB的距离相等.
由条件易得平面PAB且
.
