1.2空间几何体的三视图和直观图同步课时作业-2021-2022学年高一下学期数学人教A版必修2(word含解析)
文档属性
| 名称 | 1.2空间几何体的三视图和直观图同步课时作业-2021-2022学年高一下学期数学人教A版必修2(word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 557.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 10:35:24 | ||
图片预览



文档简介
1.2 空间几何体的三视图和直观图-2021-2022学年高一数学人教A版必修2同步课时作业
1.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:)是( )
A. B. C. D.
2.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )
A.9 B. C.11 D.
3.已知某几何体的三视图如图所示,则该几何体的表面积为( )
A. B. C. D.
4.已知一个几何体的三视图如图所示,其外接球的表面积为,则这个几何体的体积为( )
A.20 B.16 C.20或12 D.16或20
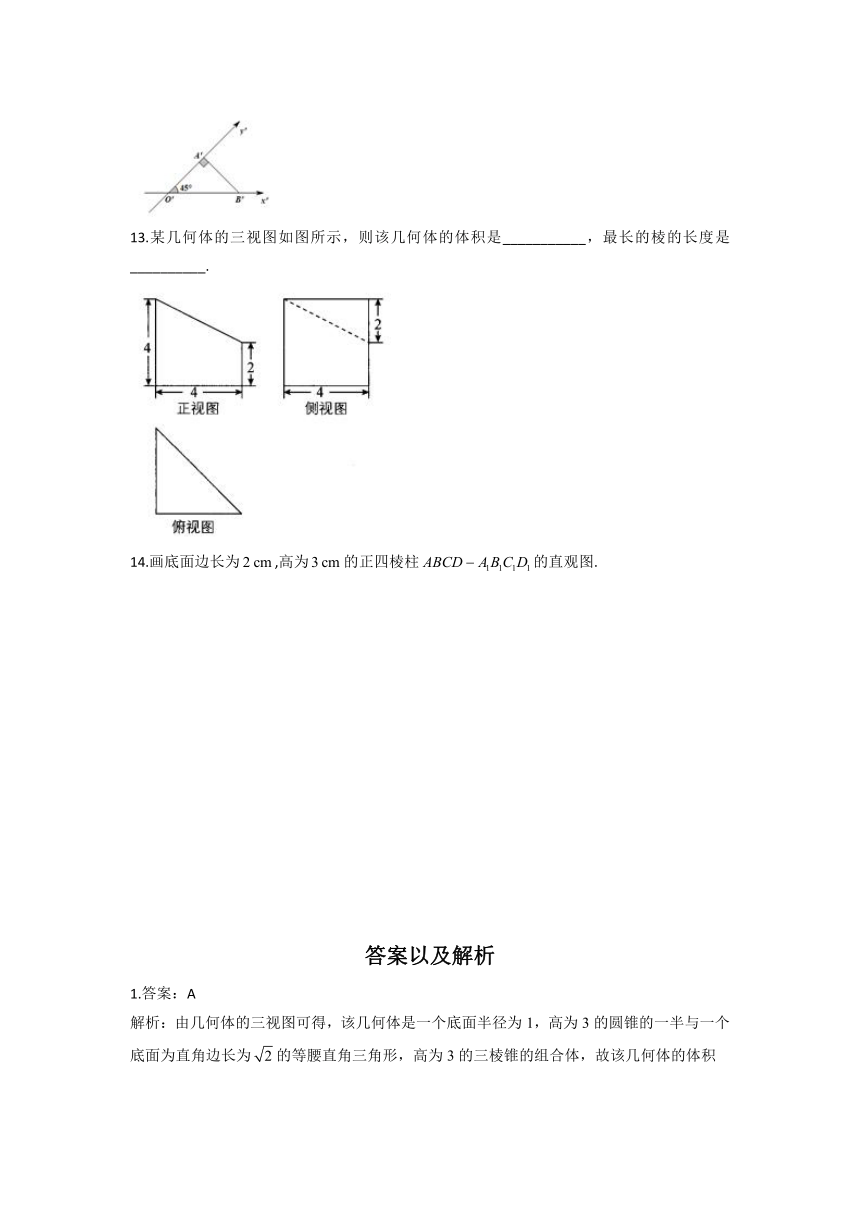
5.已知水平放置的四边形按斜二测画法得到如图所示的直观图,其中,,,,则原四边形的面积为( )
A. B. C. D.
6.下图为某旋转体的三视图,则该几何体的侧面积为( )
A. B. C. D.
7.已知某几何体的三视图如图所示,则该几何体的最长棱的长度为( )
A. B. C. D.
8.某几何体的三视图如图所示,其中正视图中的曲线为圆弧,则该几何体的表面积为( )
A. B. C. D.
9.如图,平行四边形是水平放置的一个平面图形的直观图,其中,则下列叙述正确的是( )
A.原图形是正方形 B.原图形是非正方形的菱形
C.原图形的面积是 D.原图形的面积是
10.如图是六个棱长为1的正方块组成的一个几何体,它的左视图的面积是( )
A.6 B.5 C.4 D.3
11.某四面体的三视图如图所示.该四面体的六条棱中,最大长度是______.
12.如图,已知等腰直角三角形是一个平面图形的直观图,且,斜边,则这个平面图形的面积是________.
13.某几何体的三视图如图所示,则该几何体的体积是___________,最长的棱的长度是__________.
14.画底面边长为,高为的正四棱柱的直观图.
答案以及解析
1.答案:A
解析:由几何体的三视图可得,该几何体是一个底面半径为1,高为3的圆锥的一半与一个底面为直角边长为的等腰直角三角形,高为3的三棱锥的组合体,故该几何体的体积.
2.答案:C
解析:由三视图可知该几何体是在底面为边长是2的正方形、高是3的直四棱柱的基础上,截去一个底面积为,高为3的三棱锥形成的,该几何体如图所示.
,所以.
3.答案:A
解析:根据三视图知,该几何体是底面为直角梯形的四棱锥,且侧棱底面ABCD;画出图形,如图所示:
结合图中数据,计算该几何体的表面积为:
.
4.答案:D
解析:根据趣意,外接球的直径为,该几何体可看作长方体截得的一部分,如下图两种图形,该几何体外接球的直径为长方体的体对角线长,设长方体底面的宽为x,,,故该几何体的体积为或.故选D.
5.答案:B
解析:过点作,垂足为
则由已知可得四边形为矩形,为等腰直角三角形
,
根据直观图画出原图如下:
可得原图形为直角梯形,,
且,
可得原四边形的面积为
故选:B.
6.答案:D
解析:由三视图知:几何体为底面半径为1,高为3的圆锥体,
其侧面展开为以底面周长为弧长,圆锥体母线长为半径的扇形,
故几何体的侧面积为.
7.答案:C
解析:由三视图可得原几何体为右图所示的三棱锥,,,,,该几何体的最长棱为.
8.答案:D
解析:根据三视图知,该几何体是棱长为 4 的正 方体,截去一个 圆柱体,如图所示;
结合图中数据,计算该几何体的表面积为
故选 : D.
9.答案:C
解析:将直观图还原为平面图形,如图所示,可以发现原平而图形不是菱形,故A,B均错误;,,故C正确,D错误.
10.答案:D
解析:解:从左边看,底层有2个正方形,上层右边有1个正方形,共3个正方形,因为棱长为1,所以面积为3.
11.答案:
解析:由三视图可知原几何体为三棱锥,
其中底面为俯视图中的钝角三角形,为钝角,
其中,BC边上的高为,底面ABC,且,
由以上条件可知,为直角,最长的棱为PA或AB,
在直角三角形PAC中,由勾股定理得,
又在钝角三角形ABC中,,
故四面体的六条棱中,最大长度是.故答案为:.
12.答案:
解析:如图所示,因为是一个平面图形的直观图,其中斜边,所以,
根据斜二测画法的规则,可得,所以直角的面积为.
13.答案:;6
解析:本题考查由三视图还原几何体并求几何体的体积和最长的棱的长度.由三视图可知该几何体是由一个底面为等腰直角三角形的直三棱柱截去一个三棱锥得到的,如图所示,
且侧棱
所以该几何体的体积为
最长的棱为.
14.答案:如图D-8-22.
(1)建立空间直角坐标系﹔
(2)在轴上作线段,在轴上作线段;
(3)过作轴的平行线,过作轴的平行线,使得两条平行线交于点;
(4)作,分别过作轴的平行线,使得
(5)连接则四棱柱就是要作的直观图.
1.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:)是( )
A. B. C. D.
2.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )
A.9 B. C.11 D.
3.已知某几何体的三视图如图所示,则该几何体的表面积为( )
A. B. C. D.
4.已知一个几何体的三视图如图所示,其外接球的表面积为,则这个几何体的体积为( )
A.20 B.16 C.20或12 D.16或20
5.已知水平放置的四边形按斜二测画法得到如图所示的直观图,其中,,,,则原四边形的面积为( )
A. B. C. D.
6.下图为某旋转体的三视图,则该几何体的侧面积为( )
A. B. C. D.
7.已知某几何体的三视图如图所示,则该几何体的最长棱的长度为( )
A. B. C. D.
8.某几何体的三视图如图所示,其中正视图中的曲线为圆弧,则该几何体的表面积为( )
A. B. C. D.
9.如图,平行四边形是水平放置的一个平面图形的直观图,其中,则下列叙述正确的是( )
A.原图形是正方形 B.原图形是非正方形的菱形
C.原图形的面积是 D.原图形的面积是
10.如图是六个棱长为1的正方块组成的一个几何体,它的左视图的面积是( )
A.6 B.5 C.4 D.3
11.某四面体的三视图如图所示.该四面体的六条棱中,最大长度是______.
12.如图,已知等腰直角三角形是一个平面图形的直观图,且,斜边,则这个平面图形的面积是________.
13.某几何体的三视图如图所示,则该几何体的体积是___________,最长的棱的长度是__________.
14.画底面边长为,高为的正四棱柱的直观图.
答案以及解析
1.答案:A
解析:由几何体的三视图可得,该几何体是一个底面半径为1,高为3的圆锥的一半与一个底面为直角边长为的等腰直角三角形,高为3的三棱锥的组合体,故该几何体的体积.
2.答案:C
解析:由三视图可知该几何体是在底面为边长是2的正方形、高是3的直四棱柱的基础上,截去一个底面积为,高为3的三棱锥形成的,该几何体如图所示.
,所以.
3.答案:A
解析:根据三视图知,该几何体是底面为直角梯形的四棱锥,且侧棱底面ABCD;画出图形,如图所示:
结合图中数据,计算该几何体的表面积为:
.
4.答案:D
解析:根据趣意,外接球的直径为,该几何体可看作长方体截得的一部分,如下图两种图形,该几何体外接球的直径为长方体的体对角线长,设长方体底面的宽为x,,,故该几何体的体积为或.故选D.
5.答案:B
解析:过点作,垂足为
则由已知可得四边形为矩形,为等腰直角三角形
,
根据直观图画出原图如下:
可得原图形为直角梯形,,
且,
可得原四边形的面积为
故选:B.
6.答案:D
解析:由三视图知:几何体为底面半径为1,高为3的圆锥体,
其侧面展开为以底面周长为弧长,圆锥体母线长为半径的扇形,
故几何体的侧面积为.
7.答案:C
解析:由三视图可得原几何体为右图所示的三棱锥,,,,,该几何体的最长棱为.
8.答案:D
解析:根据三视图知,该几何体是棱长为 4 的正 方体,截去一个 圆柱体,如图所示;
结合图中数据,计算该几何体的表面积为
故选 : D.
9.答案:C
解析:将直观图还原为平面图形,如图所示,可以发现原平而图形不是菱形,故A,B均错误;,,故C正确,D错误.
10.答案:D
解析:解:从左边看,底层有2个正方形,上层右边有1个正方形,共3个正方形,因为棱长为1,所以面积为3.
11.答案:
解析:由三视图可知原几何体为三棱锥,
其中底面为俯视图中的钝角三角形,为钝角,
其中,BC边上的高为,底面ABC,且,
由以上条件可知,为直角,最长的棱为PA或AB,
在直角三角形PAC中,由勾股定理得,
又在钝角三角形ABC中,,
故四面体的六条棱中,最大长度是.故答案为:.
12.答案:
解析:如图所示,因为是一个平面图形的直观图,其中斜边,所以,
根据斜二测画法的规则,可得,所以直角的面积为.
13.答案:;6
解析:本题考查由三视图还原几何体并求几何体的体积和最长的棱的长度.由三视图可知该几何体是由一个底面为等腰直角三角形的直三棱柱截去一个三棱锥得到的,如图所示,
且侧棱
所以该几何体的体积为
最长的棱为.
14.答案:如图D-8-22.
(1)建立空间直角坐标系﹔
(2)在轴上作线段,在轴上作线段;
(3)过作轴的平行线,过作轴的平行线,使得两条平行线交于点;
(4)作,分别过作轴的平行线,使得
(5)连接则四棱柱就是要作的直观图.
