5.1.2导数的概念及其几何意义(第二课时)课件(46张ppt)
文档属性
| 名称 | 5.1.2导数的概念及其几何意义(第二课时)课件(46张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 15.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 00:00:00 | ||
图片预览






文档简介
(共46张PPT)
讲课老师:关老师
学习目标
理解导数的几何意义;
根据导数的几何意义,会求曲线上某点的切线方程;
了解导函数的概念;
会求导函数;
知识回顾
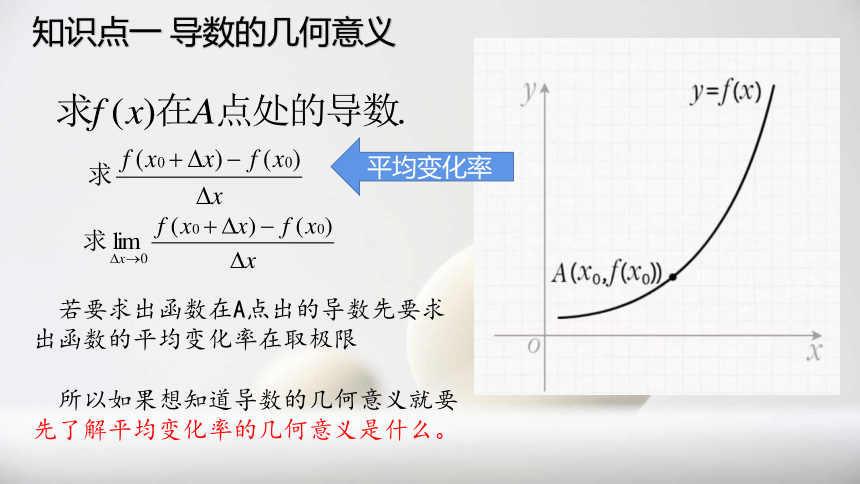
由导数的意义可知,求函数 在点x0处的导数的就基本步骤是:
平均变化率
若要求出函数在A点出的导数先要求出函数的平均变化率在取极限
所以如果想知道导数的几何意义就要先了解平均变化率的几何意义是什么。
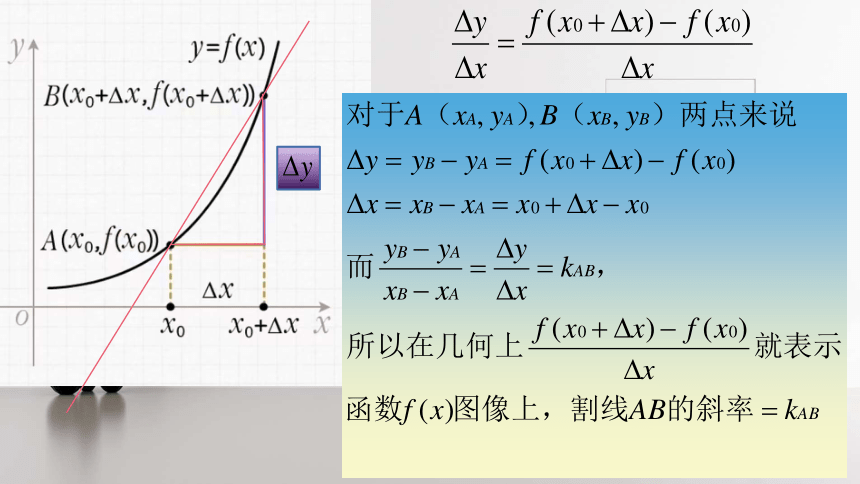
A
B
o
x
y
y=f(x)
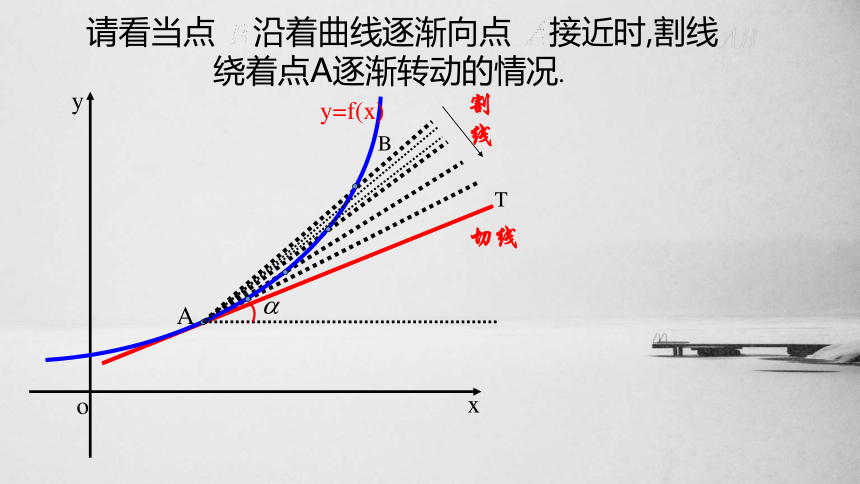
割线
切线
T
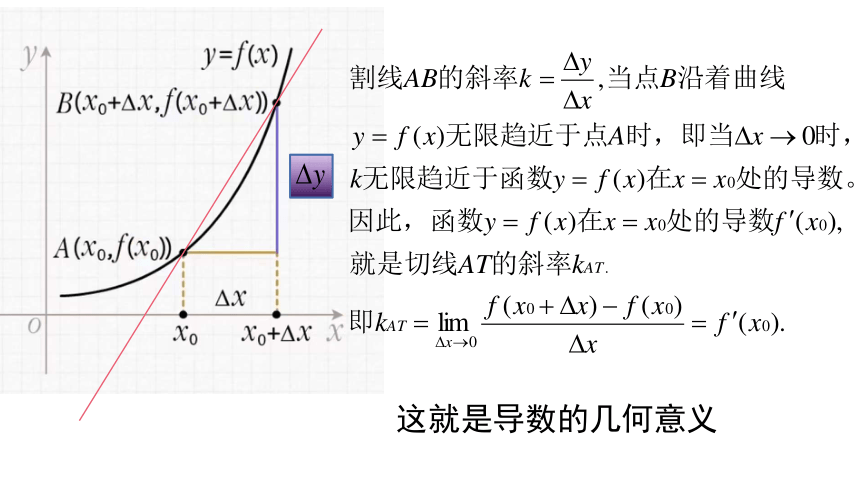
请看当点 沿着曲线逐渐向点 接近时,割线 绕着点A逐渐转动的情况.
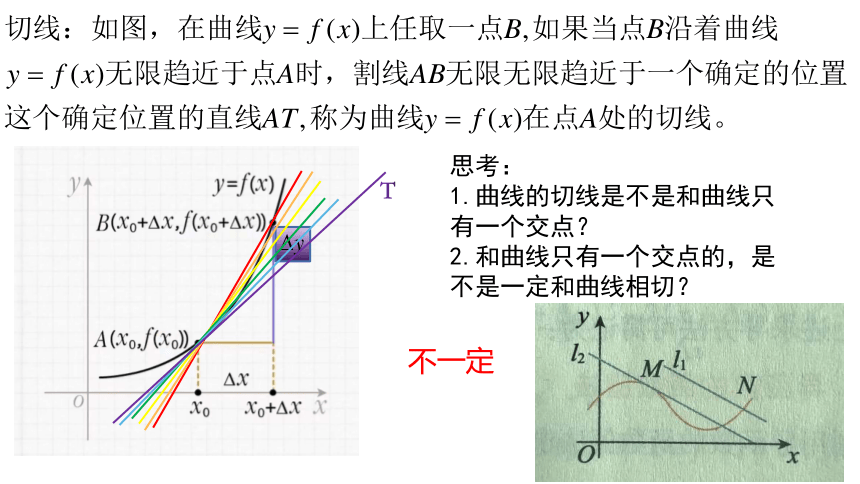
思考:
1.曲线的切线是不是和曲线只有一个交点?
2.和曲线只有一个交点的,是不是一定和曲线相切?
不一定
小牛试刀(判断正误)
1.直线与曲线相切,则直线与已知曲线只有一个公共点;
2.过曲线上的一点作曲线的切线,这点一定是切点。
这就是导数的几何意义
思考:那经过该点的切线方程怎么求?
点斜式
1.求出切点
2.求导,求出切线的斜率
切线方程
点斜式
小牛试刀
题型一 导数几何意义与函数图象
[例1] (1)若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x)在区间[a,b]上的图象可能是( )
[分析] 导数的几何意义是什么?y=f(x)的导函数在区间[a,b]上是增函数,说明y=f(x)图象的切线有什么特点?
[解析] 因为函数y=f(x)的导函数y=f′(x)在[a,b]上是增函数,由导数的几何意义可知,在区间[a,b]上各点处的切线斜率是逐渐增大的,只有A选项符合.
[答案] A
[分析] 解答此类问题的关键是理解导函数的意义.
[答案] 2m
1.f′(x0)即为过曲线y=f(x)上点P(x0,f(x0))切线的斜率.
2.曲线的升降、切线的斜率与导数符号的关系如下表:
曲线f(x)在x=x0附近的升降情况 切线的
斜率k 切线的
倾斜角
f′(x0)>0 上升 k>0 锐角
f′(x0)<0 下降 k<0 钝角
f′(x0)=0 平坦 k=0 零角(切线与x轴平行)
说明:切线斜率的绝对值的大小反映了曲线在相应点附近上升或下降的快慢.
3.若f′(x)是在区间(a,b)上的增函数,则f(x)的图象是向下凸的,如例题(1)中图A.若f′(x)在(a,b)上是减函数,则f(x)的图象是向上凸的,如例题(1)中图B.若f′(x)是在区间(a,b)上的常函数,则f(x)图象是一条线段,如例题(1)中图C.
题型二 求曲线的切线方程
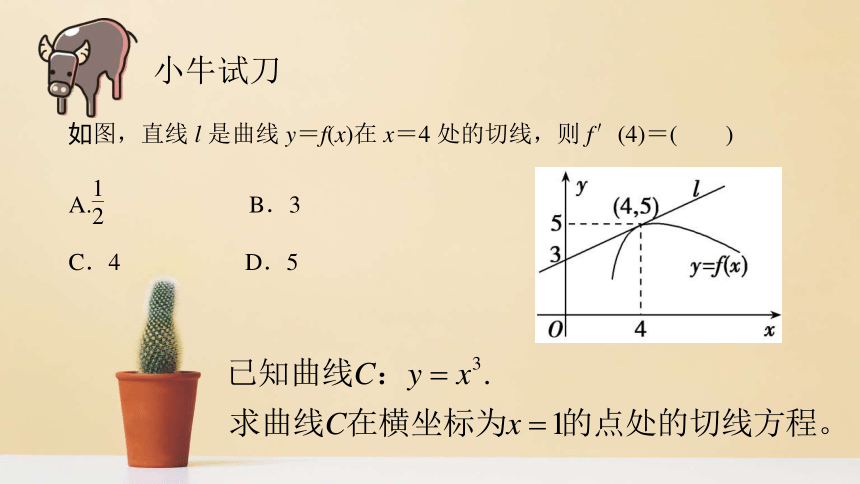
[例2] 已知曲线C:y=x3.
(1)求曲线C在横坐标为x=1的点处的切线方程;
(2)求曲线C过点P(1,1)的切线方程.
利用导数的几何意义求切线方程的方法
(1)若已知点(x0,y0)在已知曲线上,求在点(x0,y0)处的切线方程,先求出函数y=f(x)在点x0处的导数,然后根据直线的点斜式方程,得切线方程y-y0=f′(x0)(x-x0).
(2)若点(x0,y0)不在曲线上,求过点(x0,y0)的切线方程,首先应设出切点坐标,然后根据导数的几何意义列出等式,求出切点坐标,进而求出切线方程.
题型三 求切点坐标
[例3] 已知抛物线y=2x2+1.求:
(1)抛物线上哪一点的切线的倾斜角为45°?
(2)抛物线上哪一点的切线平行于直线4x-y-2=0
(2)∵抛物线的切线平行于直线4x-y-2=0,
∴斜率为4,
即f′(x0)=4x0=4,得x0=1,该点为(1,3).
根据切线斜率求切点坐标的步骤
(1)设切点坐标(x0,y0);
(2)求导函数f′(x);
(3)求切线的斜率f′(x0);
(4)由斜率间的关系列出关于x0的方程,解方程求x0;
(5)点(x0,y0)在曲线f(x)上,将(x0,y0)代入求y0得切点坐标.
微思考:导函数是什么?似乎就是关于导数的函数。可具体该怎么理解呢
还是挺简单的吧!
下面计算当x=2时
找出在解题步骤中出现的自变量x,你发现了什么?
除了自变量x的取值不同,求导的方法步骤,几乎完全一样
作差
求平均变化率
取极限
步骤综合起来
就像一个大型的
求导机器
输入一个自变量x=1,产生一个导数值
输入另一个变量x=-2,又产生一个导数值
因为始终是同一个f(x)
所以除了自变量,步骤也全部相同。
既然定义域内的每个值都是这么算的,我们每次都重复求导过程的话,就非常的麻烦,不如一开始,就输入一个任意的自变量x0,求出函数在x0处的导数,以后在求某一点的导数,直接给xo赋值就可以了。
想求哪个点的导数,就带哪个点到x0里就可以。
对比一下导数的定义和导函数的定义非常相似,不过你发现哪里不同?
v
区别:
在计算某点处的导数值,是给这个点一个增量,x0是一个具体的数,求完的导数值也是一个具体的数。
而计算导函数,是给自变量x一个增量,是从一个函数,算到一个新的函数,而不是具体的数。
所以在求某一点的导数,就不用一个一个算了,可以直接计算出函数的导函数,然后借助导函数研究每一个点的导数
提示:
导函数也简称导数,所以如果题目让你计算函数的导数,一般就是计算它的导函数。
小牛试刀
[素养提升] 导数几何意义的综合应用
(1)导数的几何意义是曲线的切线斜率,已知切点可以求斜率,已知斜率也可以求切点.
(2)导数几何意义的综合应用题目的解题关键是求函数在某点处的导数,即切线的斜率.注意结合相关知识(如函数、方程、不等式等)求解.
综上,过点P(2,4)的切线方程为x-y+2=0或4x-y-4=0.
[答案] x-y+2=0或4x-y-4=0
[误区警示] 求曲线的切线方程时,要看清题目是“求曲线在某点处的切线方程”,还是“求曲线过某点的切线方程”.前者的切线有且只有一条,而后者有可能有一条或多条.如图(1)所示,过点P(点P不在曲线上)的切线有l1,l2两条.如图(2)所示,即使点在曲线上,过点Q的切线也有l3,l4两条,其切点分别为Q,C.
小结
讲课老师:关老师
学习目标
理解导数的几何意义;
根据导数的几何意义,会求曲线上某点的切线方程;
了解导函数的概念;
会求导函数;
知识回顾
由导数的意义可知,求函数 在点x0处的导数的就基本步骤是:
平均变化率
若要求出函数在A点出的导数先要求出函数的平均变化率在取极限
所以如果想知道导数的几何意义就要先了解平均变化率的几何意义是什么。
A
B
o
x
y
y=f(x)
割线
切线
T
请看当点 沿着曲线逐渐向点 接近时,割线 绕着点A逐渐转动的情况.
思考:
1.曲线的切线是不是和曲线只有一个交点?
2.和曲线只有一个交点的,是不是一定和曲线相切?
不一定
小牛试刀(判断正误)
1.直线与曲线相切,则直线与已知曲线只有一个公共点;
2.过曲线上的一点作曲线的切线,这点一定是切点。
这就是导数的几何意义
思考:那经过该点的切线方程怎么求?
点斜式
1.求出切点
2.求导,求出切线的斜率
切线方程
点斜式
小牛试刀
题型一 导数几何意义与函数图象
[例1] (1)若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x)在区间[a,b]上的图象可能是( )
[分析] 导数的几何意义是什么?y=f(x)的导函数在区间[a,b]上是增函数,说明y=f(x)图象的切线有什么特点?
[解析] 因为函数y=f(x)的导函数y=f′(x)在[a,b]上是增函数,由导数的几何意义可知,在区间[a,b]上各点处的切线斜率是逐渐增大的,只有A选项符合.
[答案] A
[分析] 解答此类问题的关键是理解导函数的意义.
[答案] 2m
1.f′(x0)即为过曲线y=f(x)上点P(x0,f(x0))切线的斜率.
2.曲线的升降、切线的斜率与导数符号的关系如下表:
曲线f(x)在x=x0附近的升降情况 切线的
斜率k 切线的
倾斜角
f′(x0)>0 上升 k>0 锐角
f′(x0)<0 下降 k<0 钝角
f′(x0)=0 平坦 k=0 零角(切线与x轴平行)
说明:切线斜率的绝对值的大小反映了曲线在相应点附近上升或下降的快慢.
3.若f′(x)是在区间(a,b)上的增函数,则f(x)的图象是向下凸的,如例题(1)中图A.若f′(x)在(a,b)上是减函数,则f(x)的图象是向上凸的,如例题(1)中图B.若f′(x)是在区间(a,b)上的常函数,则f(x)图象是一条线段,如例题(1)中图C.
题型二 求曲线的切线方程
[例2] 已知曲线C:y=x3.
(1)求曲线C在横坐标为x=1的点处的切线方程;
(2)求曲线C过点P(1,1)的切线方程.
利用导数的几何意义求切线方程的方法
(1)若已知点(x0,y0)在已知曲线上,求在点(x0,y0)处的切线方程,先求出函数y=f(x)在点x0处的导数,然后根据直线的点斜式方程,得切线方程y-y0=f′(x0)(x-x0).
(2)若点(x0,y0)不在曲线上,求过点(x0,y0)的切线方程,首先应设出切点坐标,然后根据导数的几何意义列出等式,求出切点坐标,进而求出切线方程.
题型三 求切点坐标
[例3] 已知抛物线y=2x2+1.求:
(1)抛物线上哪一点的切线的倾斜角为45°?
(2)抛物线上哪一点的切线平行于直线4x-y-2=0
(2)∵抛物线的切线平行于直线4x-y-2=0,
∴斜率为4,
即f′(x0)=4x0=4,得x0=1,该点为(1,3).
根据切线斜率求切点坐标的步骤
(1)设切点坐标(x0,y0);
(2)求导函数f′(x);
(3)求切线的斜率f′(x0);
(4)由斜率间的关系列出关于x0的方程,解方程求x0;
(5)点(x0,y0)在曲线f(x)上,将(x0,y0)代入求y0得切点坐标.
微思考:导函数是什么?似乎就是关于导数的函数。可具体该怎么理解呢
还是挺简单的吧!
下面计算当x=2时
找出在解题步骤中出现的自变量x,你发现了什么?
除了自变量x的取值不同,求导的方法步骤,几乎完全一样
作差
求平均变化率
取极限
步骤综合起来
就像一个大型的
求导机器
输入一个自变量x=1,产生一个导数值
输入另一个变量x=-2,又产生一个导数值
因为始终是同一个f(x)
所以除了自变量,步骤也全部相同。
既然定义域内的每个值都是这么算的,我们每次都重复求导过程的话,就非常的麻烦,不如一开始,就输入一个任意的自变量x0,求出函数在x0处的导数,以后在求某一点的导数,直接给xo赋值就可以了。
想求哪个点的导数,就带哪个点到x0里就可以。
对比一下导数的定义和导函数的定义非常相似,不过你发现哪里不同?
v
区别:
在计算某点处的导数值,是给这个点一个增量,x0是一个具体的数,求完的导数值也是一个具体的数。
而计算导函数,是给自变量x一个增量,是从一个函数,算到一个新的函数,而不是具体的数。
所以在求某一点的导数,就不用一个一个算了,可以直接计算出函数的导函数,然后借助导函数研究每一个点的导数
提示:
导函数也简称导数,所以如果题目让你计算函数的导数,一般就是计算它的导函数。
小牛试刀
[素养提升] 导数几何意义的综合应用
(1)导数的几何意义是曲线的切线斜率,已知切点可以求斜率,已知斜率也可以求切点.
(2)导数几何意义的综合应用题目的解题关键是求函数在某点处的导数,即切线的斜率.注意结合相关知识(如函数、方程、不等式等)求解.
综上,过点P(2,4)的切线方程为x-y+2=0或4x-y-4=0.
[答案] x-y+2=0或4x-y-4=0
[误区警示] 求曲线的切线方程时,要看清题目是“求曲线在某点处的切线方程”,还是“求曲线过某点的切线方程”.前者的切线有且只有一条,而后者有可能有一条或多条.如图(1)所示,过点P(点P不在曲线上)的切线有l1,l2两条.如图(2)所示,即使点在曲线上,过点Q的切线也有l3,l4两条,其切点分别为Q,C.
小结
