第二十四章 圆综合复习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学圆综合复习
一.垂径定理(共5小题)
1.如图,在⊙O中,CD是⊙O的直径,AB⊥CD于点E,若AB=8,CE=2,则⊙O的半径为( )
A. B. C.3 D.5
2.如图,⊙O的直径AB⊥弦CD于点E,连接BD.若CD=8,OE=3,则BD的长为( )
A. B.2 C. D.2
3.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=8cm,CD=8cm,则BE为( )
A.1 B.1.5 C.2 D.2.5
4.如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP,AO分别与⊙O交于B,C两点,若⊙O的半径为3,OP=,则弦BC的最大值为 .
5.如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是 .
二.圆心角、弧、弦的关系(共5小题)
6.已知点O,C在直线m的同一侧,作⊙O交m于点A,B.连结AC,BC,OA,OB,若点C在⊙O外,∠AOB=110°,则∠C的角度可能是( )
A.50° B.55° C.60° D.65°
7.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=3,⊙O的直径为15,则AC长为( )
A.10 B.13 C.12 D.11
8.如图,在半径为13的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=24,则OP的长是 .
9.如图,⊙O的弦AC=BD,且AC⊥BD于点E,连接AB,若⊙O的半径是3cm,则AB的长是 cm.
10.如图,在⊙O中,AC=AB,直径BC=2,,则AD= .
三.圆周角定理(共4小题)
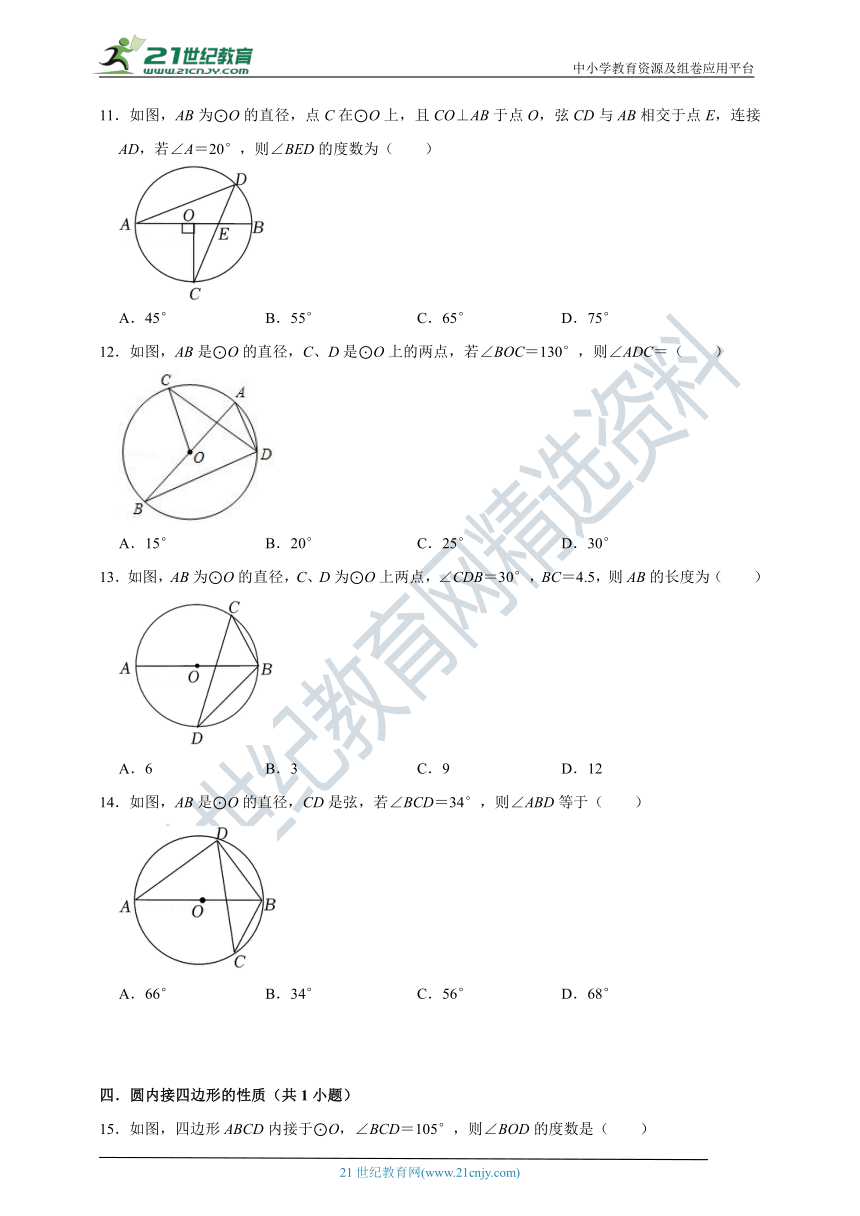
11.如图,AB为⊙O的直径,点C在⊙O上,且CO⊥AB于点O,弦CD与AB相交于点E,连接AD,若∠A=20°,则∠BED的度数为( )
A.45° B.55° C.65° D.75°
12.如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠BOC=130°,则∠ADC=( )
A.15° B.20° C.25° D.30°
13.如图,AB为⊙O的直径,C、D为⊙O上两点,∠CDB=30°,BC=4.5,则AB的长度为( )
A.6 B.3 C.9 D.12
14.如图,AB是⊙O的直径,CD是弦,若∠BCD=34°,则∠ABD等于( )
A.66° B.34° C.56° D.68°
四.圆内接四边形的性质(共1小题)
15.如图,四边形ABCD内接于⊙O,∠BCD=105°,则∠BOD的度数是( )
A.150° B.120° C.105° D.85°
五.切线的性质(共2小题)
16.如图,PA、PB是⊙O的切线,A、B是切点,点C在⊙O上,且∠ACB=56°,则∠APB等于( )
A.58° B.68° C.78° D.124°
17.如图,PA是⊙O的切线,A为切点,连接OP交⊙O于点C,点B在⊙O上,且∠ABC=24°,则∠APC等于( )
A.31° B.42° C.53° D.64°
六.切线的判定与性质(共2小题)
18.已知,如图,AB为圆O直径,AC=FC,E为弧BD中点.
(1)求证:AC为圆O切线;
(2)若AB=4,AC=3,求DF的长.
19.如图,点C在以AB为直径的⊙O上,AC平分∠BAD,且AD⊥CD于点D.
(1)求证:DC是⊙O的切线;
(2)若AD=4,CD=2,求⊙O的半径.
七.三角形的内切圆与内心(共1小题)
20.如图,△ABC中,∠C=90°,AC=12,BC=5,⊙O与△ABC的三边相切于点D、E、F,则AD长为( )
A.8 B.10 C.12 D.14
八.正多边形和圆(共5小题)
21.如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D重合),则∠CPD的度数为( )
A.72° B.60° C.36° D.30°
22.如图,正五边形ABCDE内接于⊙O,则∠CBD的度数是( )
A.30° B.36° C.60° D.72°
23.一个圆的内接正多边形中,一条边所对的圆心角为72°,则该正多边形的边数是( )
A.4 B.5 C.6 D.7
24.正六边形的边长为2,⊙O是它的内切圆,则⊙O的面积为( )
A.2π B.π C. D.3π
25.如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P,则∠APN的度数为( )
A.120° B.118° C.110° D.108°
九.弧长的计算(共3小题)
26.若120°的圆心角所对的弧长是2π,则此弧所在圆的半径为( )
A.1 B.2 C.3 D.4
27.如图,AB是半圆O的直径,C、D是半圆上两点,且满足∠ADC=120°,BC=1,则的长为( )
A. B. C. D.
28.如图,AB为⊙O的直径,AB=4,CD=2,劣弧BC的长是劣弧BD长的2倍,则AC的长为( )
A. B. C.3 D.
一十.弧长的计算(共1小题)
29.如图,四边形ABCD内接于⊙O,AE是⊙O的直径.若⊙O的半径为6,∠ADC﹣∠ABC=40°,则的长度为( )
A. B. C. D.
一十一.圆锥的计算(共2小题)
30.已知圆锥的母线长为6,侧面展开图的面积是12π,则这个圆锥底面圆的半径是( )
A.1 B.2 C.3 D.4
31.如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=3cm,△ABC绕AC所在直线旋转一周,所形成的圆锥侧面积等于( )
A.4πcm2 B.8πcm2 C.12πcm2 D.15πcm2
参考答案与试题解析
一.垂径定理(共5小题)
1.如图,在⊙O中,CD是⊙O的直径,AB⊥CD于点E,若AB=8,CE=2,则⊙O的半径为( )
A. B. C.3 D.5
【解答】解:设⊙O的半径为r,
∵CD是⊙O的直径,AB⊥CD,AB=8,
∴AE=AB=4,
在Rt△OAE中,由勾股定理得:AE2+OE2=OA2,
即42+(r﹣2)2=r2,
解得:r=5,
即⊙O的半径为5,
故选:D.
2.如图,⊙O的直径AB⊥弦CD于点E,连接BD.若CD=8,OE=3,则BD的长为( )
A. B.2 C. D.2
【解答】解:
连接OD,
∵AB⊥CD,AB过圆心O,CD=8,
∴CE=DE=4,∠OED=∠DEB=90°,
∵OE=3,
∴OD===5,
∴OB=OD=5,
∴BE=OB﹣OE=5﹣3=2,
由勾股定理,得BD====2,
故选:D.
3.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=8cm,CD=8cm,则BE为( )
A.1 B.1.5 C.2 D.2.5
【解答】解:∵CD⊥AB,
∴CE=DE=CD=4cm,
设⊙O的半径为rcm,则OC=rcm,OE=(8﹣r)cm,
在Rt△OCE中,(8﹣r)2+42=r2,
解得r=5,
∴OE=8﹣5=3(cm),
∴BE=OB﹣OE=5﹣3=2(cm).
故选:C.
4.如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP,AO分别与⊙O交于B,C两点,若⊙O的半径为3,OP=,则弦BC的最大值为 2 .
【解答】解:如图,过点O作OE⊥AB于E,
∵O为圆心,
∴AE=BE,
∴OE=BC,
∵OE≤OP,
∴BC≤2OP,
∴当E、P重合时,即OP垂直AB时,BC取最大值,
∴弦BC的最大值为:2OP=2,
故答案为:2.
5.如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是 .
【解答】解:如图,作△AEC的外接圆⊙O′,延长BC交⊙O′于D2R,连接AR,则AR是直径,连接OO′,EO′.
∵EC⊥CD,
∴∠ECD=90°,
∵AB是直径,
∴∠ACB=90°,
∴BC===4,
∵∠D+∠DEC=90°,∠B+∠BAC=90°,∠B=∠D,
∴∠DEC=∠BAC=定值,
∴∠AEC是定值,
∴点E的运动轨迹是,
∵∠R+∠AEC=180°,∠AEC+∠DEC=180°,
∴∠R=∠DEC=∠BAC,
∴∠R+∠B=90°,
∴∠BAR=90°,
∵∠B=∠B,∠ACB=∠BAR=90°,
∴△BCA∽△BAR,
∴=,
∴=,
∴BR=,
∴CR=BR﹣BC=,
∴AR===,
∴EO′=AR=,
∵AO=OB,AO′=O′R,
∴OO′=BR=,
∵OE≥OO′﹣EO′=﹣=,
∴OE的最小值为.
故答案为:.
二.圆心角、弧、弦的关系(共5小题)
6.已知点O,C在直线m的同一侧,作⊙O交m于点A,B.连结AC,BC,OA,OB,若点C在⊙O外,∠AOB=110°,则∠C的角度可能是( )
A.50° B.55° C.60° D.65°
【解答】解:如图,设⊙O交AC于点T,连接BT.
∵∠ATB=∠AOB=55°,
又∵∠ATB>∠C,
∴∠C<55°,
故选:A.
7.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=3,⊙O的直径为15,则AC长为( )
A.10 B.13 C.12 D.11
【解答】解:连接OF,
∵DE⊥AB,AB过圆心O,
∴DE=EF,=,
∵D为弧AC的中点,
∴=,
∴=,
∴AC=DF,
∵⊙O的直径为15,
∴OF=OA=,
∵AE=3,
∴OE=OA﹣AE=,
在Rt△OEF中,由勾股定理得:EF===6,
∴DE=EF=6,
∴AC=DF=DE+EF=6+6=12,
故选:C.
8.如图,在半径为13的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=24,则OP的长是 5 .
【解答】解:作OM⊥AB于M,ON⊥CD于N,连接OB,OD,
由垂径定理、勾股定理得:OM=ON==5,
∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=5
故答案为:5.
9.如图,⊙O的弦AC=BD,且AC⊥BD于点E,连接AB,若⊙O的半径是3cm,则AB的长是 cm.
【解答】解:连接AD,OA,OB,
∵AC=BD,
∴弧AC=弧BD,
∴弧AC﹣弧BC=弧BD﹣弧BC,
即弧AB=弧CD,
∴∠ADB=∠CAD,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADB=∠CAD=45°,
∴∠AOB=2∠ADB=90°,
∴AB=.
10.如图,在⊙O中,AC=AB,直径BC=2,,则AD= 3 .
【解答】解:如图,连接DB,DC,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵BC是直径,
∴∠BAC=90°,
∵BC=2,AB=2AC,
∴AC=2,AB=4,
∵∠DEA=∠EAF=∠DFA=90°,
∴四边形DEAF是矩形,
∵AD平分∠BAC,
∴DE=DF,
∴四边形DEAF是正方形,
∴AD=AF,
∵∠DAB=∠DAC,
∴=,
∴BD=CD,
∵∠DEB=∠F=90°,DB=DC,DE=DF,
∴Rt△DEB≌Rt△DFC(HL),
∴BE=CF,
∴AB+AC=AE+BE=AF﹣CF=2AF=6,
∴AF=3,
∴AD=AF=3,
故答案为:3.
三.圆周角定理(共4小题)
11.如图,AB为⊙O的直径,点C在⊙O上,且CO⊥AB于点O,弦CD与AB相交于点E,连接AD,若∠A=20°,则∠BED的度数为( )
A.45° B.55° C.65° D.75°
【解答】解:∵OC⊥AB,
∴∠COA=90°,
∴∠D=∠COA=45°,
∵∠BED=∠D+∠A,∠A=20°,
∴∠BED=45°+20°=65°,
故选:C.
12.如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠BOC=130°,则∠ADC=( )
A.15° B.20° C.25° D.30°
【解答】解:∵∠AOC=180°﹣∠BOC=180°﹣130°=50°,
∴∠ADC=∠AOC=25°,
故选:C.
13.如图,AB为⊙O的直径,C、D为⊙O上两点,∠CDB=30°,BC=4.5,则AB的长度为( )
A.6 B.3 C.9 D.12
【解答】解:如图,连接AC.
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAB=∠CDB=30°,BC=4.5,
∴AB=2BC=9,
故选:C.
14.如图,AB是⊙O的直径,CD是弦,若∠BCD=34°,则∠ABD等于( )
A.66° B.34° C.56° D.68°
【解答】解:连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∵∠DAB=∠BCD=34°,
∴∠ABD=90°﹣34°=56°,
故选:C.
四.圆内接四边形的性质(共1小题)
15.如图,四边形ABCD内接于⊙O,∠BCD=105°,则∠BOD的度数是( )
A.150° B.120° C.105° D.85°
【解答】解:如图,四边形ABCD内接于⊙O,∠BCD=105°,则∠A=180°﹣∠BCD=180°﹣105°=75°.
∴∠BOD=2∠A=2×75°=150°,
故选:A.
五.切线的性质(共2小题)
16.如图,PA、PB是⊙O的切线,A、B是切点,点C在⊙O上,且∠ACB=56°,则∠APB等于( )
A.58° B.68° C.78° D.124°
【解答】解:连接OA、OB,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
由圆周角定理:∠AOB=2∠ACB=2×56°=112°,
∴∠APB=360°﹣90°﹣90°﹣112°=68°,
故选:B.
17.如图,PA是⊙O的切线,A为切点,连接OP交⊙O于点C,点B在⊙O上,且∠ABC=24°,则∠APC等于( )
A.31° B.42° C.53° D.64°
【解答】解:连接OA,
∵∠ABC=24°,
∴∠AOC=2∠ABC=48°,
∵PA是⊙O的切线,
∴∠OAP=90°,
∴∠APC=90°﹣∠AOP=42°,
故选:B.
六.切线的判定与性质(共2小题)
18.已知,如图,AB为圆O直径,AC=FC,E为弧BD中点.
(1)求证:AC为圆O切线;
(2)若AB=4,AC=3,求DF的长.
【解答】(1)证明:如图1,连接BE,
∵E为弧BD中点,
∴=,
∴∠DBE=∠BAE,
∵AB为⊙O直径,
∴∠AEB=90°,
∴∠DBE+∠BFE=90°,
∴∠BAE+∠BFE=90°,
∵∠BFE=∠CFA,
∴∠BAE+∠CFA=90°,
∵AC=FC,
∴∠CAF=∠CFA,
∴∠BAE+∠CAF=90°,
∴AB⊥AC,
∵AB是⊙O的直径,
∴AC为⊙O切线;
(2)如图2,连接AD,过点F作FG⊥AB于点G,
由(1)知:∠BAC=90°,
∴BC===5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴BC AD=AB AC,
∴AD===,
∴BD===,
∵=,
∴∠DAE=∠BAE,
∵FD⊥AD,FG⊥AB,
∴FD=FG,设FD=FG=x,
∵S△ABD=S△ADF+S△ABF,
∴××=×x+×4x,
解得:x=,
∴DF=.
19.如图,点C在以AB为直径的⊙O上,AC平分∠BAD,且AD⊥CD于点D.
(1)求证:DC是⊙O的切线;
(2)若AD=4,CD=2,求⊙O的半径.
【解答】(1)证明:如图中,连接OC.
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠DAC=∠CAB=∠ACO,
∴AD∥OC,
∵AD⊥CD,
∴OC⊥DC,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)解:如图,过点O作OE⊥AD于点E,
得矩形OEDC,
∴OE=CD=2,DE=OC,
∴AE=AD﹣DE=4﹣OC=4﹣OA,
在Rt△AEO中,根据勾股定理,得
OA2=AE2+OE2,
∴OA2=(4﹣OA)2+22,
解得OA=.
∴⊙O的半径为.
七.三角形的内切圆与内心(共1小题)
20.如图,△ABC中,∠C=90°,AC=12,BC=5,⊙O与△ABC的三边相切于点D、E、F,则AD长为( )
A.8 B.10 C.12 D.14
【解答】解:如图,连接OD、OE、OF,
∵∠C=90°,AC=12,BC=5,
∴AB===13,
设OE=OF=OD=r,
∵S△ABC=S△AOB+S△BOC+S△AOC,
∴13r+12r+5r=12×5,
解得r=2,
∵⊙O与Rt△ABC的三边相切于点D、E、F,
∴OE⊥AC,OF⊥BC,
∴四边形OECF为正方形,
∵⊙O的半径为2,BC=5,
∴CE=CF=2,BD=BF=3,
∴AD=AB﹣BD=13﹣3=10.
故选:B.
八.正多边形和圆(共5小题)
21.如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D重合),则∠CPD的度数为( )
A.72° B.60° C.36° D.30°
【解答】解:如图,连接OC,OD.
∵多边形ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
故选:C.
22.如图,正五边形ABCDE内接于⊙O,则∠CBD的度数是( )
A.30° B.36° C.60° D.72°
【解答】解:∵正五边形ABCDE内接于⊙O,
∴CD=BC==108°,
∴∠CBD=∠CDB=(180°﹣108°)=36°,
故选:B.
23.一个圆的内接正多边形中,一条边所对的圆心角为72°,则该正多边形的边数是( )
A.4 B.5 C.6 D.7
【解答】解:设正多边形的边数为n.
由题意可得:=72°,
∴n=5,
故选:B.
24.正六边形的边长为2,⊙O是它的内切圆,则⊙O的面积为( )
A.2π B.π C. D.3π
【解答】解:如图,连接OA、OB,OG;
∵六边形ABCDEF是边长为4的正六边形,
∴△OAB是等边三角形,
∴OA=AB=2,
∴OG=OA sin60°=2×=,
∴边长为2的正六边形的内切圆的半径为,
∴内切圆面积为π×()2=3π.
故选:D.
25.如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P,则∠APN的度数为( )
A.120° B.118° C.110° D.108°
【解答】:∵五边形ABCDE为正五边形,
∴AB=BC,∠ABM=∠C,
在△ABM和△BCN中,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC==108°,
∴∠APN的度数为108°;
故选:D.
九.弧长的计算(共3小题)
26.若120°的圆心角所对的弧长是2π,则此弧所在圆的半径为( )
A.1 B.2 C.3 D.4
【解答】解:由题意得,n=120°,l=2π,
故可得:,
解得:r=3.
故选:C.
27.如图,AB是半圆O的直径,C、D是半圆上两点,且满足∠ADC=120°,BC=1,则的长为( )
A. B. C. D.
【解答】解:如图,连接OC.
∵∠ADC=120°,
∴∠ABC=60°,
∵OB=OC,
∴∠OCB=∠OBC=∠B=60°,
OB=OC=BC=1,
∴的长为=,
故选:A.
28.如图,AB为⊙O的直径,AB=4,CD=2,劣弧BC的长是劣弧BD长的2倍,则AC的长为( )
A. B. C.3 D.
【解答】解:如图,连接OC、OD、BC.
∵AB为⊙O的直径,AB=4,
∴∠ACB=90°,OC=OD=AB=2,
∵CD=2,
∴OC2+OD2=22+22=8=CD2,
∴∠COD=90°,
∵劣弧BC的长是劣弧BD长的2倍,
∴∠COB=2∠BOD,
∴∠COB=∠COD=×90°=60°,
∴∠A=∠COB=30°.
在Rt△ABC中,
AC=AB cosA=4×=2.
故选:D.
一十.弧长的计算(共1小题)
29.如图,四边形ABCD内接于⊙O,AE是⊙O的直径.若⊙O的半径为6,∠ADC﹣∠ABC=40°,则的长度为( )
A. B. C. D.
【解答】解:如图,连接OC.
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∵∠ADC﹣∠ABC=40°,
∴∠ADC=110°,∠ABC=70°.
∴∠AOC=2∠ABC=140°,
∴∠COE=180°﹣∠AOC=40°,
∵⊙O的半径为6,
∴的长度为=.
故选:B.
一十一.圆锥的计算(共2小题)
30.已知圆锥的母线长为6,侧面展开图的面积是12π,则这个圆锥底面圆的半径是( )
A.1 B.2 C.3 D.4
【解答】解:设这个圆锥底面圆的半径为r,
根据题意得×2πr×6=12π,
解得r=2,
即这个圆锥底面圆的半径是2.
故选:B.
31.如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=3cm,△ABC绕AC所在直线旋转一周,所形成的圆锥侧面积等于( )
A.4πcm2 B.8πcm2 C.12πcm2 D.15πcm2
【解答】解:根据题意,△ABC绕AC所在直线旋转一周,所形成的圆锥侧面积=×2π×3×5=15π(cm2).
故选:D.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学圆综合复习
一.垂径定理(共5小题)
1.如图,在⊙O中,CD是⊙O的直径,AB⊥CD于点E,若AB=8,CE=2,则⊙O的半径为( )
A. B. C.3 D.5
2.如图,⊙O的直径AB⊥弦CD于点E,连接BD.若CD=8,OE=3,则BD的长为( )
A. B.2 C. D.2
3.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=8cm,CD=8cm,则BE为( )
A.1 B.1.5 C.2 D.2.5
4.如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP,AO分别与⊙O交于B,C两点,若⊙O的半径为3,OP=,则弦BC的最大值为 .
5.如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是 .
二.圆心角、弧、弦的关系(共5小题)
6.已知点O,C在直线m的同一侧,作⊙O交m于点A,B.连结AC,BC,OA,OB,若点C在⊙O外,∠AOB=110°,则∠C的角度可能是( )
A.50° B.55° C.60° D.65°
7.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=3,⊙O的直径为15,则AC长为( )
A.10 B.13 C.12 D.11
8.如图,在半径为13的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=24,则OP的长是 .
9.如图,⊙O的弦AC=BD,且AC⊥BD于点E,连接AB,若⊙O的半径是3cm,则AB的长是 cm.
10.如图,在⊙O中,AC=AB,直径BC=2,,则AD= .
三.圆周角定理(共4小题)
11.如图,AB为⊙O的直径,点C在⊙O上,且CO⊥AB于点O,弦CD与AB相交于点E,连接AD,若∠A=20°,则∠BED的度数为( )
A.45° B.55° C.65° D.75°
12.如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠BOC=130°,则∠ADC=( )
A.15° B.20° C.25° D.30°
13.如图,AB为⊙O的直径,C、D为⊙O上两点,∠CDB=30°,BC=4.5,则AB的长度为( )
A.6 B.3 C.9 D.12
14.如图,AB是⊙O的直径,CD是弦,若∠BCD=34°,则∠ABD等于( )
A.66° B.34° C.56° D.68°
四.圆内接四边形的性质(共1小题)
15.如图,四边形ABCD内接于⊙O,∠BCD=105°,则∠BOD的度数是( )
A.150° B.120° C.105° D.85°
五.切线的性质(共2小题)
16.如图,PA、PB是⊙O的切线,A、B是切点,点C在⊙O上,且∠ACB=56°,则∠APB等于( )
A.58° B.68° C.78° D.124°
17.如图,PA是⊙O的切线,A为切点,连接OP交⊙O于点C,点B在⊙O上,且∠ABC=24°,则∠APC等于( )
A.31° B.42° C.53° D.64°
六.切线的判定与性质(共2小题)
18.已知,如图,AB为圆O直径,AC=FC,E为弧BD中点.
(1)求证:AC为圆O切线;
(2)若AB=4,AC=3,求DF的长.
19.如图,点C在以AB为直径的⊙O上,AC平分∠BAD,且AD⊥CD于点D.
(1)求证:DC是⊙O的切线;
(2)若AD=4,CD=2,求⊙O的半径.
七.三角形的内切圆与内心(共1小题)
20.如图,△ABC中,∠C=90°,AC=12,BC=5,⊙O与△ABC的三边相切于点D、E、F,则AD长为( )
A.8 B.10 C.12 D.14
八.正多边形和圆(共5小题)
21.如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D重合),则∠CPD的度数为( )
A.72° B.60° C.36° D.30°
22.如图,正五边形ABCDE内接于⊙O,则∠CBD的度数是( )
A.30° B.36° C.60° D.72°
23.一个圆的内接正多边形中,一条边所对的圆心角为72°,则该正多边形的边数是( )
A.4 B.5 C.6 D.7
24.正六边形的边长为2,⊙O是它的内切圆,则⊙O的面积为( )
A.2π B.π C. D.3π
25.如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P,则∠APN的度数为( )
A.120° B.118° C.110° D.108°
九.弧长的计算(共3小题)
26.若120°的圆心角所对的弧长是2π,则此弧所在圆的半径为( )
A.1 B.2 C.3 D.4
27.如图,AB是半圆O的直径,C、D是半圆上两点,且满足∠ADC=120°,BC=1,则的长为( )
A. B. C. D.
28.如图,AB为⊙O的直径,AB=4,CD=2,劣弧BC的长是劣弧BD长的2倍,则AC的长为( )
A. B. C.3 D.
一十.弧长的计算(共1小题)
29.如图,四边形ABCD内接于⊙O,AE是⊙O的直径.若⊙O的半径为6,∠ADC﹣∠ABC=40°,则的长度为( )
A. B. C. D.
一十一.圆锥的计算(共2小题)
30.已知圆锥的母线长为6,侧面展开图的面积是12π,则这个圆锥底面圆的半径是( )
A.1 B.2 C.3 D.4
31.如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=3cm,△ABC绕AC所在直线旋转一周,所形成的圆锥侧面积等于( )
A.4πcm2 B.8πcm2 C.12πcm2 D.15πcm2
参考答案与试题解析
一.垂径定理(共5小题)
1.如图,在⊙O中,CD是⊙O的直径,AB⊥CD于点E,若AB=8,CE=2,则⊙O的半径为( )
A. B. C.3 D.5
【解答】解:设⊙O的半径为r,
∵CD是⊙O的直径,AB⊥CD,AB=8,
∴AE=AB=4,
在Rt△OAE中,由勾股定理得:AE2+OE2=OA2,
即42+(r﹣2)2=r2,
解得:r=5,
即⊙O的半径为5,
故选:D.
2.如图,⊙O的直径AB⊥弦CD于点E,连接BD.若CD=8,OE=3,则BD的长为( )
A. B.2 C. D.2
【解答】解:
连接OD,
∵AB⊥CD,AB过圆心O,CD=8,
∴CE=DE=4,∠OED=∠DEB=90°,
∵OE=3,
∴OD===5,
∴OB=OD=5,
∴BE=OB﹣OE=5﹣3=2,
由勾股定理,得BD====2,
故选:D.
3.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=8cm,CD=8cm,则BE为( )
A.1 B.1.5 C.2 D.2.5
【解答】解:∵CD⊥AB,
∴CE=DE=CD=4cm,
设⊙O的半径为rcm,则OC=rcm,OE=(8﹣r)cm,
在Rt△OCE中,(8﹣r)2+42=r2,
解得r=5,
∴OE=8﹣5=3(cm),
∴BE=OB﹣OE=5﹣3=2(cm).
故选:C.
4.如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP,AO分别与⊙O交于B,C两点,若⊙O的半径为3,OP=,则弦BC的最大值为 2 .
【解答】解:如图,过点O作OE⊥AB于E,
∵O为圆心,
∴AE=BE,
∴OE=BC,
∵OE≤OP,
∴BC≤2OP,
∴当E、P重合时,即OP垂直AB时,BC取最大值,
∴弦BC的最大值为:2OP=2,
故答案为:2.
5.如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是 .
【解答】解:如图,作△AEC的外接圆⊙O′,延长BC交⊙O′于D2R,连接AR,则AR是直径,连接OO′,EO′.
∵EC⊥CD,
∴∠ECD=90°,
∵AB是直径,
∴∠ACB=90°,
∴BC===4,
∵∠D+∠DEC=90°,∠B+∠BAC=90°,∠B=∠D,
∴∠DEC=∠BAC=定值,
∴∠AEC是定值,
∴点E的运动轨迹是,
∵∠R+∠AEC=180°,∠AEC+∠DEC=180°,
∴∠R=∠DEC=∠BAC,
∴∠R+∠B=90°,
∴∠BAR=90°,
∵∠B=∠B,∠ACB=∠BAR=90°,
∴△BCA∽△BAR,
∴=,
∴=,
∴BR=,
∴CR=BR﹣BC=,
∴AR===,
∴EO′=AR=,
∵AO=OB,AO′=O′R,
∴OO′=BR=,
∵OE≥OO′﹣EO′=﹣=,
∴OE的最小值为.
故答案为:.
二.圆心角、弧、弦的关系(共5小题)
6.已知点O,C在直线m的同一侧,作⊙O交m于点A,B.连结AC,BC,OA,OB,若点C在⊙O外,∠AOB=110°,则∠C的角度可能是( )
A.50° B.55° C.60° D.65°
【解答】解:如图,设⊙O交AC于点T,连接BT.
∵∠ATB=∠AOB=55°,
又∵∠ATB>∠C,
∴∠C<55°,
故选:A.
7.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=3,⊙O的直径为15,则AC长为( )
A.10 B.13 C.12 D.11
【解答】解:连接OF,
∵DE⊥AB,AB过圆心O,
∴DE=EF,=,
∵D为弧AC的中点,
∴=,
∴=,
∴AC=DF,
∵⊙O的直径为15,
∴OF=OA=,
∵AE=3,
∴OE=OA﹣AE=,
在Rt△OEF中,由勾股定理得:EF===6,
∴DE=EF=6,
∴AC=DF=DE+EF=6+6=12,
故选:C.
8.如图,在半径为13的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=24,则OP的长是 5 .
【解答】解:作OM⊥AB于M,ON⊥CD于N,连接OB,OD,
由垂径定理、勾股定理得:OM=ON==5,
∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=5
故答案为:5.
9.如图,⊙O的弦AC=BD,且AC⊥BD于点E,连接AB,若⊙O的半径是3cm,则AB的长是 cm.
【解答】解:连接AD,OA,OB,
∵AC=BD,
∴弧AC=弧BD,
∴弧AC﹣弧BC=弧BD﹣弧BC,
即弧AB=弧CD,
∴∠ADB=∠CAD,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADB=∠CAD=45°,
∴∠AOB=2∠ADB=90°,
∴AB=.
10.如图,在⊙O中,AC=AB,直径BC=2,,则AD= 3 .
【解答】解:如图,连接DB,DC,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵BC是直径,
∴∠BAC=90°,
∵BC=2,AB=2AC,
∴AC=2,AB=4,
∵∠DEA=∠EAF=∠DFA=90°,
∴四边形DEAF是矩形,
∵AD平分∠BAC,
∴DE=DF,
∴四边形DEAF是正方形,
∴AD=AF,
∵∠DAB=∠DAC,
∴=,
∴BD=CD,
∵∠DEB=∠F=90°,DB=DC,DE=DF,
∴Rt△DEB≌Rt△DFC(HL),
∴BE=CF,
∴AB+AC=AE+BE=AF﹣CF=2AF=6,
∴AF=3,
∴AD=AF=3,
故答案为:3.
三.圆周角定理(共4小题)
11.如图,AB为⊙O的直径,点C在⊙O上,且CO⊥AB于点O,弦CD与AB相交于点E,连接AD,若∠A=20°,则∠BED的度数为( )
A.45° B.55° C.65° D.75°
【解答】解:∵OC⊥AB,
∴∠COA=90°,
∴∠D=∠COA=45°,
∵∠BED=∠D+∠A,∠A=20°,
∴∠BED=45°+20°=65°,
故选:C.
12.如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠BOC=130°,则∠ADC=( )
A.15° B.20° C.25° D.30°
【解答】解:∵∠AOC=180°﹣∠BOC=180°﹣130°=50°,
∴∠ADC=∠AOC=25°,
故选:C.
13.如图,AB为⊙O的直径,C、D为⊙O上两点,∠CDB=30°,BC=4.5,则AB的长度为( )
A.6 B.3 C.9 D.12
【解答】解:如图,连接AC.
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAB=∠CDB=30°,BC=4.5,
∴AB=2BC=9,
故选:C.
14.如图,AB是⊙O的直径,CD是弦,若∠BCD=34°,则∠ABD等于( )
A.66° B.34° C.56° D.68°
【解答】解:连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∵∠DAB=∠BCD=34°,
∴∠ABD=90°﹣34°=56°,
故选:C.
四.圆内接四边形的性质(共1小题)
15.如图,四边形ABCD内接于⊙O,∠BCD=105°,则∠BOD的度数是( )
A.150° B.120° C.105° D.85°
【解答】解:如图,四边形ABCD内接于⊙O,∠BCD=105°,则∠A=180°﹣∠BCD=180°﹣105°=75°.
∴∠BOD=2∠A=2×75°=150°,
故选:A.
五.切线的性质(共2小题)
16.如图,PA、PB是⊙O的切线,A、B是切点,点C在⊙O上,且∠ACB=56°,则∠APB等于( )
A.58° B.68° C.78° D.124°
【解答】解:连接OA、OB,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
由圆周角定理:∠AOB=2∠ACB=2×56°=112°,
∴∠APB=360°﹣90°﹣90°﹣112°=68°,
故选:B.
17.如图,PA是⊙O的切线,A为切点,连接OP交⊙O于点C,点B在⊙O上,且∠ABC=24°,则∠APC等于( )
A.31° B.42° C.53° D.64°
【解答】解:连接OA,
∵∠ABC=24°,
∴∠AOC=2∠ABC=48°,
∵PA是⊙O的切线,
∴∠OAP=90°,
∴∠APC=90°﹣∠AOP=42°,
故选:B.
六.切线的判定与性质(共2小题)
18.已知,如图,AB为圆O直径,AC=FC,E为弧BD中点.
(1)求证:AC为圆O切线;
(2)若AB=4,AC=3,求DF的长.
【解答】(1)证明:如图1,连接BE,
∵E为弧BD中点,
∴=,
∴∠DBE=∠BAE,
∵AB为⊙O直径,
∴∠AEB=90°,
∴∠DBE+∠BFE=90°,
∴∠BAE+∠BFE=90°,
∵∠BFE=∠CFA,
∴∠BAE+∠CFA=90°,
∵AC=FC,
∴∠CAF=∠CFA,
∴∠BAE+∠CAF=90°,
∴AB⊥AC,
∵AB是⊙O的直径,
∴AC为⊙O切线;
(2)如图2,连接AD,过点F作FG⊥AB于点G,
由(1)知:∠BAC=90°,
∴BC===5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴BC AD=AB AC,
∴AD===,
∴BD===,
∵=,
∴∠DAE=∠BAE,
∵FD⊥AD,FG⊥AB,
∴FD=FG,设FD=FG=x,
∵S△ABD=S△ADF+S△ABF,
∴××=×x+×4x,
解得:x=,
∴DF=.
19.如图,点C在以AB为直径的⊙O上,AC平分∠BAD,且AD⊥CD于点D.
(1)求证:DC是⊙O的切线;
(2)若AD=4,CD=2,求⊙O的半径.
【解答】(1)证明:如图中,连接OC.
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠DAC=∠CAB=∠ACO,
∴AD∥OC,
∵AD⊥CD,
∴OC⊥DC,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)解:如图,过点O作OE⊥AD于点E,
得矩形OEDC,
∴OE=CD=2,DE=OC,
∴AE=AD﹣DE=4﹣OC=4﹣OA,
在Rt△AEO中,根据勾股定理,得
OA2=AE2+OE2,
∴OA2=(4﹣OA)2+22,
解得OA=.
∴⊙O的半径为.
七.三角形的内切圆与内心(共1小题)
20.如图,△ABC中,∠C=90°,AC=12,BC=5,⊙O与△ABC的三边相切于点D、E、F,则AD长为( )
A.8 B.10 C.12 D.14
【解答】解:如图,连接OD、OE、OF,
∵∠C=90°,AC=12,BC=5,
∴AB===13,
设OE=OF=OD=r,
∵S△ABC=S△AOB+S△BOC+S△AOC,
∴13r+12r+5r=12×5,
解得r=2,
∵⊙O与Rt△ABC的三边相切于点D、E、F,
∴OE⊥AC,OF⊥BC,
∴四边形OECF为正方形,
∵⊙O的半径为2,BC=5,
∴CE=CF=2,BD=BF=3,
∴AD=AB﹣BD=13﹣3=10.
故选:B.
八.正多边形和圆(共5小题)
21.如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D重合),则∠CPD的度数为( )
A.72° B.60° C.36° D.30°
【解答】解:如图,连接OC,OD.
∵多边形ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
故选:C.
22.如图,正五边形ABCDE内接于⊙O,则∠CBD的度数是( )
A.30° B.36° C.60° D.72°
【解答】解:∵正五边形ABCDE内接于⊙O,
∴CD=BC==108°,
∴∠CBD=∠CDB=(180°﹣108°)=36°,
故选:B.
23.一个圆的内接正多边形中,一条边所对的圆心角为72°,则该正多边形的边数是( )
A.4 B.5 C.6 D.7
【解答】解:设正多边形的边数为n.
由题意可得:=72°,
∴n=5,
故选:B.
24.正六边形的边长为2,⊙O是它的内切圆,则⊙O的面积为( )
A.2π B.π C. D.3π
【解答】解:如图,连接OA、OB,OG;
∵六边形ABCDEF是边长为4的正六边形,
∴△OAB是等边三角形,
∴OA=AB=2,
∴OG=OA sin60°=2×=,
∴边长为2的正六边形的内切圆的半径为,
∴内切圆面积为π×()2=3π.
故选:D.
25.如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P,则∠APN的度数为( )
A.120° B.118° C.110° D.108°
【解答】:∵五边形ABCDE为正五边形,
∴AB=BC,∠ABM=∠C,
在△ABM和△BCN中,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC==108°,
∴∠APN的度数为108°;
故选:D.
九.弧长的计算(共3小题)
26.若120°的圆心角所对的弧长是2π,则此弧所在圆的半径为( )
A.1 B.2 C.3 D.4
【解答】解:由题意得,n=120°,l=2π,
故可得:,
解得:r=3.
故选:C.
27.如图,AB是半圆O的直径,C、D是半圆上两点,且满足∠ADC=120°,BC=1,则的长为( )
A. B. C. D.
【解答】解:如图,连接OC.
∵∠ADC=120°,
∴∠ABC=60°,
∵OB=OC,
∴∠OCB=∠OBC=∠B=60°,
OB=OC=BC=1,
∴的长为=,
故选:A.
28.如图,AB为⊙O的直径,AB=4,CD=2,劣弧BC的长是劣弧BD长的2倍,则AC的长为( )
A. B. C.3 D.
【解答】解:如图,连接OC、OD、BC.
∵AB为⊙O的直径,AB=4,
∴∠ACB=90°,OC=OD=AB=2,
∵CD=2,
∴OC2+OD2=22+22=8=CD2,
∴∠COD=90°,
∵劣弧BC的长是劣弧BD长的2倍,
∴∠COB=2∠BOD,
∴∠COB=∠COD=×90°=60°,
∴∠A=∠COB=30°.
在Rt△ABC中,
AC=AB cosA=4×=2.
故选:D.
一十.弧长的计算(共1小题)
29.如图,四边形ABCD内接于⊙O,AE是⊙O的直径.若⊙O的半径为6,∠ADC﹣∠ABC=40°,则的长度为( )
A. B. C. D.
【解答】解:如图,连接OC.
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∵∠ADC﹣∠ABC=40°,
∴∠ADC=110°,∠ABC=70°.
∴∠AOC=2∠ABC=140°,
∴∠COE=180°﹣∠AOC=40°,
∵⊙O的半径为6,
∴的长度为=.
故选:B.
一十一.圆锥的计算(共2小题)
30.已知圆锥的母线长为6,侧面展开图的面积是12π,则这个圆锥底面圆的半径是( )
A.1 B.2 C.3 D.4
【解答】解:设这个圆锥底面圆的半径为r,
根据题意得×2πr×6=12π,
解得r=2,
即这个圆锥底面圆的半径是2.
故选:B.
31.如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=3cm,△ABC绕AC所在直线旋转一周,所形成的圆锥侧面积等于( )
A.4πcm2 B.8πcm2 C.12πcm2 D.15πcm2
【解答】解:根据题意,△ABC绕AC所在直线旋转一周,所形成的圆锥侧面积=×2π×3×5=15π(cm2).
故选:D.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
