18.2.1 矩形章节小测验(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
矩形章节小测
一.矩形的性质(共4小题)
1.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线垂直 C.邻边垂直 D.邻角互补
2.在矩形ABCD中,AB=6,BC=8,两对角线交于点O,则BO=( )
A.3 B.4 C.5 D.10
3.如图,在矩形ABCD中,点E是BC的中点,连接AE,点F是AE的中点,连接DF,若AB=9,AD=,则四边形CDFE的面积是( )
A. B. C. D.54
4.如图在矩形ABCD中,对角线AC,BD相交于点O,E,F分别是AO,AD的中点,若AB=12cm,BC=16cm,则EF= cm.
二.矩形的判定(共6小题)
5.如图,要使 ABCD为矩形,则可以添加的条件是( )
AC⊥BD B.AC=BD C.∠AOB=60° D.AB=BC
6.下列命题是真命题的是( )
A.有一个角是直角的四边形是矩形 B.一组对边平行且相等的四边形是矩形
C.对角线互相平分且相等的四边形是矩形 D.对角线互相垂直平分的四边形是矩形
7.如图,在平行四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=90° B.AC=BD C.AD=AB D.∠BAD=∠ADC
8.如图,在 ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( )
A.1个 B.2个 C.3个 D.4个
9.如图,在平行四边形ABCD中,AC=BC,M、N分别是AB和CD的中点.
求证:四边形AMCN是矩形.
10.如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.
(I)求证:DF∥AC;
(2)连接DE、CF,若2AB=BF,G恰好是CD的中点,求证:四边形CFDE是矩形.
三.矩形的判定与性质(共14小题)
11.下列四个命题中,正确的是( )
A.对角线相等的四边形是矩形 B.有一个角是直角的四边形是矩形
C.两组对边分别相等的四边形是矩形 D.四个角都相等的四边形是矩形
12.如图,在四边形ABCD中,AB∥CD,AB⊥BD,AB=5,BD=4,CD=3,点E是AC的中点,则BE的长为( )
A.2 B. C. D.3
13.如图,在△ABC中,∠B=90°,AB=12,BC=5,D为边AC上一动点,DE⊥AB于点E,DF⊥BC于点F,则EF的最小值为( )
A.4.8 B. C. D.13
14.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则AM的最小值是( )
A.2.4 B.2 C.1.5 D.1.2
15.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC于点D,过M作ME⊥CB于点E,则线段DE的最小值为( )
A. B.5 C. D.2.5
16.如图,在△ABC中,∠C=90°,AC=12,BC=5.P为斜边AB上一动点,过点P作PE⊥AC于点E,PF⊥BC于点F,连接EF,则线段EF的最小值为( )
B. C. D.
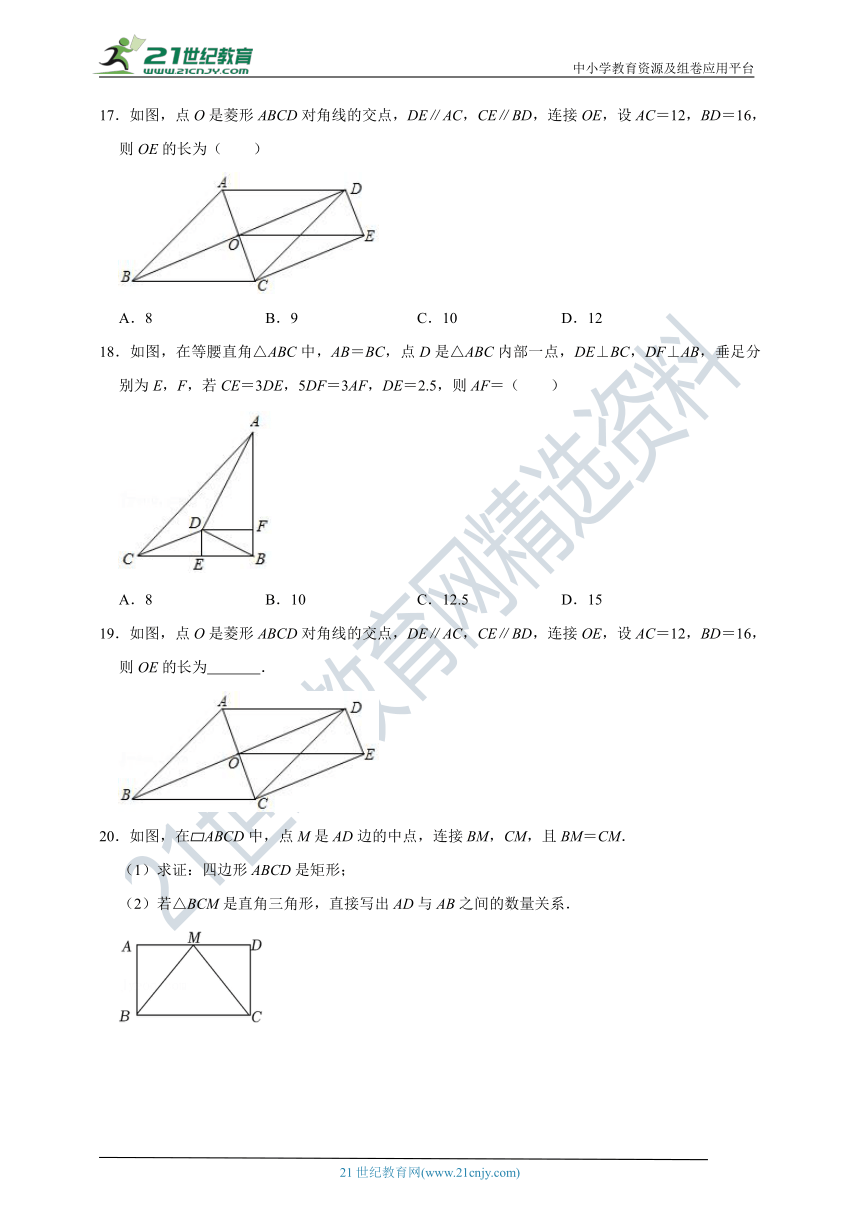
17.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
18.如图,在等腰直角△ABC中,AB=BC,点D是△ABC内部一点,DE⊥BC,DF⊥AB,垂足分别为E,F,若CE=3DE,5DF=3AF,DE=2.5,则AF=( )
A.8 B.10 C.12.5 D.15
19.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为 .
20.如图,在 ABCD中,点M是AD边的中点,连接BM,CM,且BM=CM.
(1)求证:四边形ABCD是矩形;
(2)若△BCM是直角三角形,直接写出AD与AB之间的数量关系.
21.如图,菱形ABCD的对角线AC与BD交于点O,分别过点C、点D作BD、AC的平行线交于点E,连接EO交CD于点F.
(1)求证:四边形DECO是矩形;
(2)若AD=3,求OE的长.
22.如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2时,求EA的长.
四.矩形的判定与性质(共1小题)
23.如图,在矩形ABCD中,E,F分别是边AB,AD上的动点,P是线段EF的中点,PG⊥BC,PH⊥CD,G,H为垂足,连接GH.若AB=8,AD=6,EF=6,则GH的最小值是 .
参考答案与试题解析
一.矩形的性质(共4小题)
1.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线垂直 C.邻边垂直 D.邻角互补
【解答】解:∵菱形的对角线互相垂直,但矩形的对角线不一定垂直,
∴菱形具有而矩形不一定具有的是对角线垂直,
故选:B.
2.在矩形ABCD中,AB=6,BC=8,两对角线交于点O,则BO=( )
A.3 B.4 C.5 D.10
【解答】解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC=8,OB=OD,
∴BD===10,
∴BO=BD=5;
故选:C.
3.如图,在矩形ABCD中,点E是BC的中点,连接AE,点F是AE的中点,连接DF,若AB=9,AD=,则四边形CDFE的面积是( )
A. B. C. D.54
【解答】解:过点F作直线MN,使MN⊥AD,
∵四边形ABCD是矩形,
∴∠AMF=∠ENP=90°,AD=BC=6,
∵点F是AE的中点,
∴AF=EF,
∵∠AFM=∠EFN,
∴△AFM≌△EFN(AAS),
∴MF=FN=AB=4.5,
∵点E是BC的中点,
∴BE=BC=3,
∴四边形CDFE的面积=S矩形ABCD﹣S△ABE﹣S△AFD=9×6﹣×9×3﹣×4.5×6=27,
故选:C.
4.如图在矩形ABCD中,对角线AC,BD相交于点O,E,F分别是AO,AD的中点,若AB=12cm,BC=16cm,则EF= 5 cm.
【解答】解:在Rt△ABC中,AC===20(cm),
∴矩形ABCD中,BD=20cm,DO=10cm,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
∴EF=OD==5(cm),
故答案为:5.
二.矩形的判定(共6小题)
5.如图,要使 ABCD为矩形,则可以添加的条件是( )
A.AC⊥BD B.AC=BD C.∠AOB=60° D.AB=BC
【解答】解:因为有一个角是直角的平行四边形是矩形;对角线相等的平行四边形是矩形,
故选:B.
6.下列命题是真命题的是( )
A.有一个角是直角的四边形是矩形
B.一组对边平行且相等的四边形是矩形
C.对角线互相平分且相等的四边形是矩形
D.对角线互相垂直平分的四边形是矩形
【解答】解:A、有一个角是直角的平行四边形是矩形,故原命题错误,是假命题,不符合题意;
B、一组对边平行且相等的四边形是平行四边形,故原命题错误,是假命题,不符合题意;
C、对角线互相平分且相等的四边形是矩形,正确,是真命题,符合题意;
D、对角线互相垂直平分的四边形是菱形,故原命题错误,是假命题,不符合题意,
故选:C.
7.如图,在平行四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=90° B.AC=BD C.AD=AB D.∠BAD=∠ADC
【解答】解:A.根据有一个角是直角的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意;
B.根据对角线相等的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意;
C.根据邻边相等的平行四边形是菱形能判定平行四边形ABCD为菱形,不能判定平行四边形ABCD为矩形,故此选项符合题意;
D.∵平行四边形ABCD中,AB∥CD,
∴∠BAD+∠ADC=180°,
又∵∠BAD=∠ADC,
∴∠BAD=∠ADC=90°,
根据有一个角是直角的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意.
故选:C.
8.如图,在 ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①∵∠1+∠3=90°,
∴∠ABC=90°,
∴ ABCD是矩形,故①正确;
②∵四边形ABCD是平行四边形,
∴AB=CD,
∵BC2+CD2=AC2,
∴BC2+AB2=AC2,
∴∠ABC=90°,
∴ ABCD是矩形,故②正确;
③∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵∠1=∠2,
∴OA=OB,
∴AC=BD,
∴ ABCD是矩形,故③正确;
④∵四边形ABCD是平行四边形,AC⊥BD,
∴ ABCD是菱形,故④错误;
能判定四边形ABCD是矩形的个数有3个,
故选:C.
9.如图,在平行四边形ABCD中,AC=BC,M、N分别是AB和CD的中点.
求证:四边形AMCN是矩形.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴AM∥CN,
∵M、N分别是AB和CD的中点,
∴AM=AB,CN=CD,
∴AM=CN,
∴四边形AMCN是平行四边形,
∵AC=BC,
∴△ACB是等腰三角形,
∵M是AB的中点,
∴CM是△ACB的边AB上的高,
∴∠AMC=90°,
∴平行四边形AMCN是矩形.
10.如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.
(I)求证:DF∥AC;
(2)连接DE、CF,若2AB=BF,G恰好是CD的中点,求证:四边形CFDE是矩形.
【解答】(1)证明:连接BD,交AC于点O,如图所示:
∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE=EF,
∴OE是△BDF的中位线,
∴OE∥DF,
即DF∥AC;
(2)证明:如图所示:
由(1)得:DF∥AC,
∴∠DFG=∠CEG,∠GDF=∠GCE,
∵G是CD的中点,
∴DG=CG,
在△DFG和△CEG中,
,
∴△DFG≌△CEG(AAS),
∴FG=EG,
∴四边形CFDE是平行四边形,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵2AB=BF,
∴2CD=BF,
又∵EF=BE,
∴CD=EF,
∴平行四边形CFDE是矩形.
三.矩形的判定与性质(共14小题)
11.下列四个命题中,正确的是( )
A.对角线相等的四边形是矩形
B.有一个角是直角的四边形是矩形
C.两组对边分别相等的四边形是矩形
D.四个角都相等的四边形是矩形
【解答】解:A、对角线相等的平行四边形是矩形,故原命题错误,不符合题意;
B、有一个角是直角的平行四边形是矩形,故原命题错误,不符合题意;
C、两组对边分别相等的四边形是平行四边形,故原命题错误,不符合题意;
D、四个角都相等的四边形是矩形,正确,符合题意,
故选:D.
12.如图,在四边形ABCD中,AB∥CD,AB⊥BD,AB=5,BD=4,CD=3,点E是AC的中点,则BE的长为( )
A.2 B. C. D.3
【解答】解:过点C作CF⊥AB的延长线于点F,如图所示:
∵AB∥CD,AB⊥BD,
∴CD⊥BD,
∵CF⊥AB,
∴CF⊥CD,
∴BD∥CF,
∴四边形BFCD是矩形,
∴BF=CD=3,CF=BD=4,
在Rt△BCF中,BC=,
在Rt△AFC中,AC==,
∴BC=AB=5,
∴△ABC是等腰三角形,
∵点E是AC的中点,
∴BE⊥AC,
∵,
∴×5×4=×BE,
解得:BE=.
故选:C.
13.如图,在△ABC中,∠B=90°,AB=12,BC=5,D为边AC上一动点,DE⊥AB于点E,DF⊥BC于点F,则EF的最小值为( )
A.4.8 B. C. D.13
【解答】解:如图,连接BD,
∵∠B=90°,AB=12,BC=5,
∴AC===13,
∵DE⊥AB于点E,DF⊥BC于点F,
∴四边形DEBF是矩形,
∴EF=BD,
由垂线段最短可得BD⊥AC时,线段BD最短,则EF最小,
此时,S△ABC=BC AB=AC BD,
即×12×5=×13 BD,
解得:BD=,
∴EF的最小值为.
故选:B.
14.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则AM的最小值是( )
A.2.4 B.2 C.1.5 D.1.2
【解答】解:由题意知,四边形AFPE是矩形,
∵点M是矩形对角线EF的中点,则延长AM应过点P,
∴当AP为直角三角形ABC的斜边上的高时,即AP⊥BC时,AM有最小值,
此时AM=AP,由勾股定理知BC==5,
∵S△ABC=AB AC=BC AP,
∴AP=,
∴AM=AP==1.2,
故选:D.
15.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC于点D,过M作ME⊥CB于点E,则线段DE的最小值为( )
A. B.5 C. D.2.5
【解答】解:连接CM,如图所示:
∵MD⊥AC,ME⊥CB,
∴∠MDC=∠MEC=90°,
∵∠ACB=90°,
∴四边形CDME是矩形,
∴DE=CM,
∵∠C=90°,BC=3,AC=4,
∴AB==5,
当CM⊥AB时,CM最短,此时△ABC的面积=AB CM=BC AC,
∴CM的最小值==,
∴线段DE的最小值为;
故选:A.
16.如图,在△ABC中,∠C=90°,AC=12,BC=5.P为斜边AB上一动点,过点P作PE⊥AC于点E,PF⊥BC于点F,连接EF,则线段EF的最小值为( )
A. B. C. D.
【解答】解:连接PC,如图:
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=90°,
∵∠ACB=90°,
∴四边形ECFP是矩形,
∴EF=PC,
当PC最小时,EF也最小,
∵∠ACB=90°,AC=12,BC=5,
∴AB===13,
当CP⊥AB时,PC最小,
此时,CP===,
∴线段EF长的最小值为,
故选:C.
17.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
【解答】解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故选:C.
18.如图,在等腰直角△ABC中,AB=BC,点D是△ABC内部一点,DE⊥BC,DF⊥AB,垂足分别为E,F,若CE=3DE,5DF=3AF,DE=2.5,则AF=( )
A.8 B.10 C.12.5 D.15
【解答】解:∵DE⊥BC,DF⊥AB,
∴∠DEB=∠DFB=90°,
∵△ABC为等腰直角三角形,AB=BC,
∴∠ABC=90°,
∴四边形DEBF为矩形,
∴BF=DE=2.5,DF=EB,
设DF=3x,则EB=3x,
∵5DF=3AF,
∴AF=5x,AB=5x+2.5,
∵DE=2.5,
∴CE=3DE=7.5,
∴CB=7.5+3x,
∵AB=CB,
∴5x+2.5=7.5+3x,
解得x=2.5,
∴AF=5x=12.5,
故选:C.
19.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为 10 .
【解答】解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故答案为:10.
20.如图,在 ABCD中,点M是AD边的中点,连接BM,CM,且BM=CM.
(1)求证:四边形ABCD是矩形;
(2)若△BCM是直角三角形,直接写出AD与AB之间的数量关系.
【解答】(1)证明:∵点M是AD边的中点,
∴AM=DM,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥CD,
在△ABM和△DCM中,
,
∴△ABM≌△DCM(SSS),
∴∠A=∠D,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠A=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)解:AD与AB之间的数量关系:AD=2AB,理由如下:
∵△BCM是直角三角形,BM=CM,
∴△BCM是等腰直角三角形,
∴∠MBC=45°,
由(1)得:四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠AMB=∠MBC=45°,
∴△ABM是等腰直角三角形,
∴AB=AM,
∵点M是AD边的中点,
∴AD=2AM
∴AD=2AB.
21.如图,菱形ABCD的对角线AC与BD交于点O,分别过点C、点D作BD、AC的平行线交于点E,连接EO交CD于点F.
(1)求证:四边形DECO是矩形;
(2)若AD=3,求OE的长.
【解答】(1)证明:∵CE∥BD,DE∥AC,
∴四边形DECO是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形DECO是矩形;
(2)解:∵四边形ABCD是菱形,
∴CD=AD=3,
由(1)得:四边形DECO是矩形,
∴OE=CD=3.
22.如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2时,求EA的长.
【解答】(1)证明:∵CE∥BD,DE∥AC,
∴四边形ODEC是平行四边形.
又∵菱形ABCD,
∴AC⊥BD,∴∠DOC=90°.
∴四边形ODEC是矩形.
(2)解:
四.矩形的判定与性质(共1小题)
23.如图,在矩形ABCD中,E,F分别是边AB,AD上的动点,P是线段EF的中点,PG⊥BC,PH⊥CD,G,H为垂足,连接GH.若AB=8,AD=6,EF=6,则GH的最小值是 7 .
【解答】解:连接AC、AP、CP,如图所示:
∵四边形ABCD是矩形,
∴BC=AD=6,∠BAD=∠B=∠C=90°,
∴AC===10,
∵P是线段EF的中点,
∴AP=EF=3,
∵PG⊥BC,PH⊥CD,
∴∠PGC=∠PHC=90°,
∴四边形PGCH是矩形,
∴GH=CP,
当A、P、C三点共线时,CP最小=AC﹣AP=10﹣3=7,
∴GH的最小值是7,
故答案为:7.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
矩形章节小测
一.矩形的性质(共4小题)
1.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线垂直 C.邻边垂直 D.邻角互补
2.在矩形ABCD中,AB=6,BC=8,两对角线交于点O,则BO=( )
A.3 B.4 C.5 D.10
3.如图,在矩形ABCD中,点E是BC的中点,连接AE,点F是AE的中点,连接DF,若AB=9,AD=,则四边形CDFE的面积是( )
A. B. C. D.54
4.如图在矩形ABCD中,对角线AC,BD相交于点O,E,F分别是AO,AD的中点,若AB=12cm,BC=16cm,则EF= cm.
二.矩形的判定(共6小题)
5.如图,要使 ABCD为矩形,则可以添加的条件是( )
AC⊥BD B.AC=BD C.∠AOB=60° D.AB=BC
6.下列命题是真命题的是( )
A.有一个角是直角的四边形是矩形 B.一组对边平行且相等的四边形是矩形
C.对角线互相平分且相等的四边形是矩形 D.对角线互相垂直平分的四边形是矩形
7.如图,在平行四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=90° B.AC=BD C.AD=AB D.∠BAD=∠ADC
8.如图,在 ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( )
A.1个 B.2个 C.3个 D.4个
9.如图,在平行四边形ABCD中,AC=BC,M、N分别是AB和CD的中点.
求证:四边形AMCN是矩形.
10.如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.
(I)求证:DF∥AC;
(2)连接DE、CF,若2AB=BF,G恰好是CD的中点,求证:四边形CFDE是矩形.
三.矩形的判定与性质(共14小题)
11.下列四个命题中,正确的是( )
A.对角线相等的四边形是矩形 B.有一个角是直角的四边形是矩形
C.两组对边分别相等的四边形是矩形 D.四个角都相等的四边形是矩形
12.如图,在四边形ABCD中,AB∥CD,AB⊥BD,AB=5,BD=4,CD=3,点E是AC的中点,则BE的长为( )
A.2 B. C. D.3
13.如图,在△ABC中,∠B=90°,AB=12,BC=5,D为边AC上一动点,DE⊥AB于点E,DF⊥BC于点F,则EF的最小值为( )
A.4.8 B. C. D.13
14.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则AM的最小值是( )
A.2.4 B.2 C.1.5 D.1.2
15.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC于点D,过M作ME⊥CB于点E,则线段DE的最小值为( )
A. B.5 C. D.2.5
16.如图,在△ABC中,∠C=90°,AC=12,BC=5.P为斜边AB上一动点,过点P作PE⊥AC于点E,PF⊥BC于点F,连接EF,则线段EF的最小值为( )
B. C. D.
17.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
18.如图,在等腰直角△ABC中,AB=BC,点D是△ABC内部一点,DE⊥BC,DF⊥AB,垂足分别为E,F,若CE=3DE,5DF=3AF,DE=2.5,则AF=( )
A.8 B.10 C.12.5 D.15
19.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为 .
20.如图,在 ABCD中,点M是AD边的中点,连接BM,CM,且BM=CM.
(1)求证:四边形ABCD是矩形;
(2)若△BCM是直角三角形,直接写出AD与AB之间的数量关系.
21.如图,菱形ABCD的对角线AC与BD交于点O,分别过点C、点D作BD、AC的平行线交于点E,连接EO交CD于点F.
(1)求证:四边形DECO是矩形;
(2)若AD=3,求OE的长.
22.如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2时,求EA的长.
四.矩形的判定与性质(共1小题)
23.如图,在矩形ABCD中,E,F分别是边AB,AD上的动点,P是线段EF的中点,PG⊥BC,PH⊥CD,G,H为垂足,连接GH.若AB=8,AD=6,EF=6,则GH的最小值是 .
参考答案与试题解析
一.矩形的性质(共4小题)
1.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线垂直 C.邻边垂直 D.邻角互补
【解答】解:∵菱形的对角线互相垂直,但矩形的对角线不一定垂直,
∴菱形具有而矩形不一定具有的是对角线垂直,
故选:B.
2.在矩形ABCD中,AB=6,BC=8,两对角线交于点O,则BO=( )
A.3 B.4 C.5 D.10
【解答】解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC=8,OB=OD,
∴BD===10,
∴BO=BD=5;
故选:C.
3.如图,在矩形ABCD中,点E是BC的中点,连接AE,点F是AE的中点,连接DF,若AB=9,AD=,则四边形CDFE的面积是( )
A. B. C. D.54
【解答】解:过点F作直线MN,使MN⊥AD,
∵四边形ABCD是矩形,
∴∠AMF=∠ENP=90°,AD=BC=6,
∵点F是AE的中点,
∴AF=EF,
∵∠AFM=∠EFN,
∴△AFM≌△EFN(AAS),
∴MF=FN=AB=4.5,
∵点E是BC的中点,
∴BE=BC=3,
∴四边形CDFE的面积=S矩形ABCD﹣S△ABE﹣S△AFD=9×6﹣×9×3﹣×4.5×6=27,
故选:C.
4.如图在矩形ABCD中,对角线AC,BD相交于点O,E,F分别是AO,AD的中点,若AB=12cm,BC=16cm,则EF= 5 cm.
【解答】解:在Rt△ABC中,AC===20(cm),
∴矩形ABCD中,BD=20cm,DO=10cm,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
∴EF=OD==5(cm),
故答案为:5.
二.矩形的判定(共6小题)
5.如图,要使 ABCD为矩形,则可以添加的条件是( )
A.AC⊥BD B.AC=BD C.∠AOB=60° D.AB=BC
【解答】解:因为有一个角是直角的平行四边形是矩形;对角线相等的平行四边形是矩形,
故选:B.
6.下列命题是真命题的是( )
A.有一个角是直角的四边形是矩形
B.一组对边平行且相等的四边形是矩形
C.对角线互相平分且相等的四边形是矩形
D.对角线互相垂直平分的四边形是矩形
【解答】解:A、有一个角是直角的平行四边形是矩形,故原命题错误,是假命题,不符合题意;
B、一组对边平行且相等的四边形是平行四边形,故原命题错误,是假命题,不符合题意;
C、对角线互相平分且相等的四边形是矩形,正确,是真命题,符合题意;
D、对角线互相垂直平分的四边形是菱形,故原命题错误,是假命题,不符合题意,
故选:C.
7.如图,在平行四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=90° B.AC=BD C.AD=AB D.∠BAD=∠ADC
【解答】解:A.根据有一个角是直角的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意;
B.根据对角线相等的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意;
C.根据邻边相等的平行四边形是菱形能判定平行四边形ABCD为菱形,不能判定平行四边形ABCD为矩形,故此选项符合题意;
D.∵平行四边形ABCD中,AB∥CD,
∴∠BAD+∠ADC=180°,
又∵∠BAD=∠ADC,
∴∠BAD=∠ADC=90°,
根据有一个角是直角的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意.
故选:C.
8.如图,在 ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①∵∠1+∠3=90°,
∴∠ABC=90°,
∴ ABCD是矩形,故①正确;
②∵四边形ABCD是平行四边形,
∴AB=CD,
∵BC2+CD2=AC2,
∴BC2+AB2=AC2,
∴∠ABC=90°,
∴ ABCD是矩形,故②正确;
③∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵∠1=∠2,
∴OA=OB,
∴AC=BD,
∴ ABCD是矩形,故③正确;
④∵四边形ABCD是平行四边形,AC⊥BD,
∴ ABCD是菱形,故④错误;
能判定四边形ABCD是矩形的个数有3个,
故选:C.
9.如图,在平行四边形ABCD中,AC=BC,M、N分别是AB和CD的中点.
求证:四边形AMCN是矩形.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴AM∥CN,
∵M、N分别是AB和CD的中点,
∴AM=AB,CN=CD,
∴AM=CN,
∴四边形AMCN是平行四边形,
∵AC=BC,
∴△ACB是等腰三角形,
∵M是AB的中点,
∴CM是△ACB的边AB上的高,
∴∠AMC=90°,
∴平行四边形AMCN是矩形.
10.如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.
(I)求证:DF∥AC;
(2)连接DE、CF,若2AB=BF,G恰好是CD的中点,求证:四边形CFDE是矩形.
【解答】(1)证明:连接BD,交AC于点O,如图所示:
∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE=EF,
∴OE是△BDF的中位线,
∴OE∥DF,
即DF∥AC;
(2)证明:如图所示:
由(1)得:DF∥AC,
∴∠DFG=∠CEG,∠GDF=∠GCE,
∵G是CD的中点,
∴DG=CG,
在△DFG和△CEG中,
,
∴△DFG≌△CEG(AAS),
∴FG=EG,
∴四边形CFDE是平行四边形,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵2AB=BF,
∴2CD=BF,
又∵EF=BE,
∴CD=EF,
∴平行四边形CFDE是矩形.
三.矩形的判定与性质(共14小题)
11.下列四个命题中,正确的是( )
A.对角线相等的四边形是矩形
B.有一个角是直角的四边形是矩形
C.两组对边分别相等的四边形是矩形
D.四个角都相等的四边形是矩形
【解答】解:A、对角线相等的平行四边形是矩形,故原命题错误,不符合题意;
B、有一个角是直角的平行四边形是矩形,故原命题错误,不符合题意;
C、两组对边分别相等的四边形是平行四边形,故原命题错误,不符合题意;
D、四个角都相等的四边形是矩形,正确,符合题意,
故选:D.
12.如图,在四边形ABCD中,AB∥CD,AB⊥BD,AB=5,BD=4,CD=3,点E是AC的中点,则BE的长为( )
A.2 B. C. D.3
【解答】解:过点C作CF⊥AB的延长线于点F,如图所示:
∵AB∥CD,AB⊥BD,
∴CD⊥BD,
∵CF⊥AB,
∴CF⊥CD,
∴BD∥CF,
∴四边形BFCD是矩形,
∴BF=CD=3,CF=BD=4,
在Rt△BCF中,BC=,
在Rt△AFC中,AC==,
∴BC=AB=5,
∴△ABC是等腰三角形,
∵点E是AC的中点,
∴BE⊥AC,
∵,
∴×5×4=×BE,
解得:BE=.
故选:C.
13.如图,在△ABC中,∠B=90°,AB=12,BC=5,D为边AC上一动点,DE⊥AB于点E,DF⊥BC于点F,则EF的最小值为( )
A.4.8 B. C. D.13
【解答】解:如图,连接BD,
∵∠B=90°,AB=12,BC=5,
∴AC===13,
∵DE⊥AB于点E,DF⊥BC于点F,
∴四边形DEBF是矩形,
∴EF=BD,
由垂线段最短可得BD⊥AC时,线段BD最短,则EF最小,
此时,S△ABC=BC AB=AC BD,
即×12×5=×13 BD,
解得:BD=,
∴EF的最小值为.
故选:B.
14.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则AM的最小值是( )
A.2.4 B.2 C.1.5 D.1.2
【解答】解:由题意知,四边形AFPE是矩形,
∵点M是矩形对角线EF的中点,则延长AM应过点P,
∴当AP为直角三角形ABC的斜边上的高时,即AP⊥BC时,AM有最小值,
此时AM=AP,由勾股定理知BC==5,
∵S△ABC=AB AC=BC AP,
∴AP=,
∴AM=AP==1.2,
故选:D.
15.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC于点D,过M作ME⊥CB于点E,则线段DE的最小值为( )
A. B.5 C. D.2.5
【解答】解:连接CM,如图所示:
∵MD⊥AC,ME⊥CB,
∴∠MDC=∠MEC=90°,
∵∠ACB=90°,
∴四边形CDME是矩形,
∴DE=CM,
∵∠C=90°,BC=3,AC=4,
∴AB==5,
当CM⊥AB时,CM最短,此时△ABC的面积=AB CM=BC AC,
∴CM的最小值==,
∴线段DE的最小值为;
故选:A.
16.如图,在△ABC中,∠C=90°,AC=12,BC=5.P为斜边AB上一动点,过点P作PE⊥AC于点E,PF⊥BC于点F,连接EF,则线段EF的最小值为( )
A. B. C. D.
【解答】解:连接PC,如图:
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=90°,
∵∠ACB=90°,
∴四边形ECFP是矩形,
∴EF=PC,
当PC最小时,EF也最小,
∵∠ACB=90°,AC=12,BC=5,
∴AB===13,
当CP⊥AB时,PC最小,
此时,CP===,
∴线段EF长的最小值为,
故选:C.
17.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
【解答】解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故选:C.
18.如图,在等腰直角△ABC中,AB=BC,点D是△ABC内部一点,DE⊥BC,DF⊥AB,垂足分别为E,F,若CE=3DE,5DF=3AF,DE=2.5,则AF=( )
A.8 B.10 C.12.5 D.15
【解答】解:∵DE⊥BC,DF⊥AB,
∴∠DEB=∠DFB=90°,
∵△ABC为等腰直角三角形,AB=BC,
∴∠ABC=90°,
∴四边形DEBF为矩形,
∴BF=DE=2.5,DF=EB,
设DF=3x,则EB=3x,
∵5DF=3AF,
∴AF=5x,AB=5x+2.5,
∵DE=2.5,
∴CE=3DE=7.5,
∴CB=7.5+3x,
∵AB=CB,
∴5x+2.5=7.5+3x,
解得x=2.5,
∴AF=5x=12.5,
故选:C.
19.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为 10 .
【解答】解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故答案为:10.
20.如图,在 ABCD中,点M是AD边的中点,连接BM,CM,且BM=CM.
(1)求证:四边形ABCD是矩形;
(2)若△BCM是直角三角形,直接写出AD与AB之间的数量关系.
【解答】(1)证明:∵点M是AD边的中点,
∴AM=DM,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥CD,
在△ABM和△DCM中,
,
∴△ABM≌△DCM(SSS),
∴∠A=∠D,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠A=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)解:AD与AB之间的数量关系:AD=2AB,理由如下:
∵△BCM是直角三角形,BM=CM,
∴△BCM是等腰直角三角形,
∴∠MBC=45°,
由(1)得:四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠AMB=∠MBC=45°,
∴△ABM是等腰直角三角形,
∴AB=AM,
∵点M是AD边的中点,
∴AD=2AM
∴AD=2AB.
21.如图,菱形ABCD的对角线AC与BD交于点O,分别过点C、点D作BD、AC的平行线交于点E,连接EO交CD于点F.
(1)求证:四边形DECO是矩形;
(2)若AD=3,求OE的长.
【解答】(1)证明:∵CE∥BD,DE∥AC,
∴四边形DECO是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形DECO是矩形;
(2)解:∵四边形ABCD是菱形,
∴CD=AD=3,
由(1)得:四边形DECO是矩形,
∴OE=CD=3.
22.如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2时,求EA的长.
【解答】(1)证明:∵CE∥BD,DE∥AC,
∴四边形ODEC是平行四边形.
又∵菱形ABCD,
∴AC⊥BD,∴∠DOC=90°.
∴四边形ODEC是矩形.
(2)解:
四.矩形的判定与性质(共1小题)
23.如图,在矩形ABCD中,E,F分别是边AB,AD上的动点,P是线段EF的中点,PG⊥BC,PH⊥CD,G,H为垂足,连接GH.若AB=8,AD=6,EF=6,则GH的最小值是 7 .
【解答】解:连接AC、AP、CP,如图所示:
∵四边形ABCD是矩形,
∴BC=AD=6,∠BAD=∠B=∠C=90°,
∴AC===10,
∵P是线段EF的中点,
∴AP=EF=3,
∵PG⊥BC,PH⊥CD,
∴∠PGC=∠PHC=90°,
∴四边形PGCH是矩形,
∴GH=CP,
当A、P、C三点共线时,CP最小=AC﹣AP=10﹣3=7,
∴GH的最小值是7,
故答案为:7.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
