5.1相交线与平行线 同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
相交线与平行线小测
一.选择题(共8小题)
1.如图,直线a、b被直线c所截,下列说法不正确的是( )
A.∠1与∠5是同位角 B.∠2与∠4是对顶角
C.∠3与∠6是同旁内角 D.∠5与∠2是内错角
2.如图,AC⊥BC,CD⊥AB,垂足分别为C、D,线段CD的长度是( )
A.点A到BC的距离 B.点B到AC的距离
C.点C到AB的距离 D.点D到AC的距离
3.如图,直线AB、CD相交于点O,则推导出“∠AOD=∠BOC”,下列依据中,最合理的是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等
4.下列说法正确的是( )
A.不相交的两条直线叫做平行线
B.同一平面内,过一点有且仅有一条直线与已知直线垂直
C.平角是一条直线
D.过同一平面内三点中任意两点,只能画出3条直线
5.如图,不能推出a∥b的条件是( )
A.∠4=∠2 B.∠3+∠4=180° C.∠1=∠3 D.∠2+∠3=180°
6.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠3=∠5 B.∠1=∠5 C.∠4+∠5=180° D.∠2=∠4
7.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
8.如图,下列条件①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC,∠3=∠4;④∠BAD+∠ADC=180°.其中能判定AB∥CD的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共2小题)
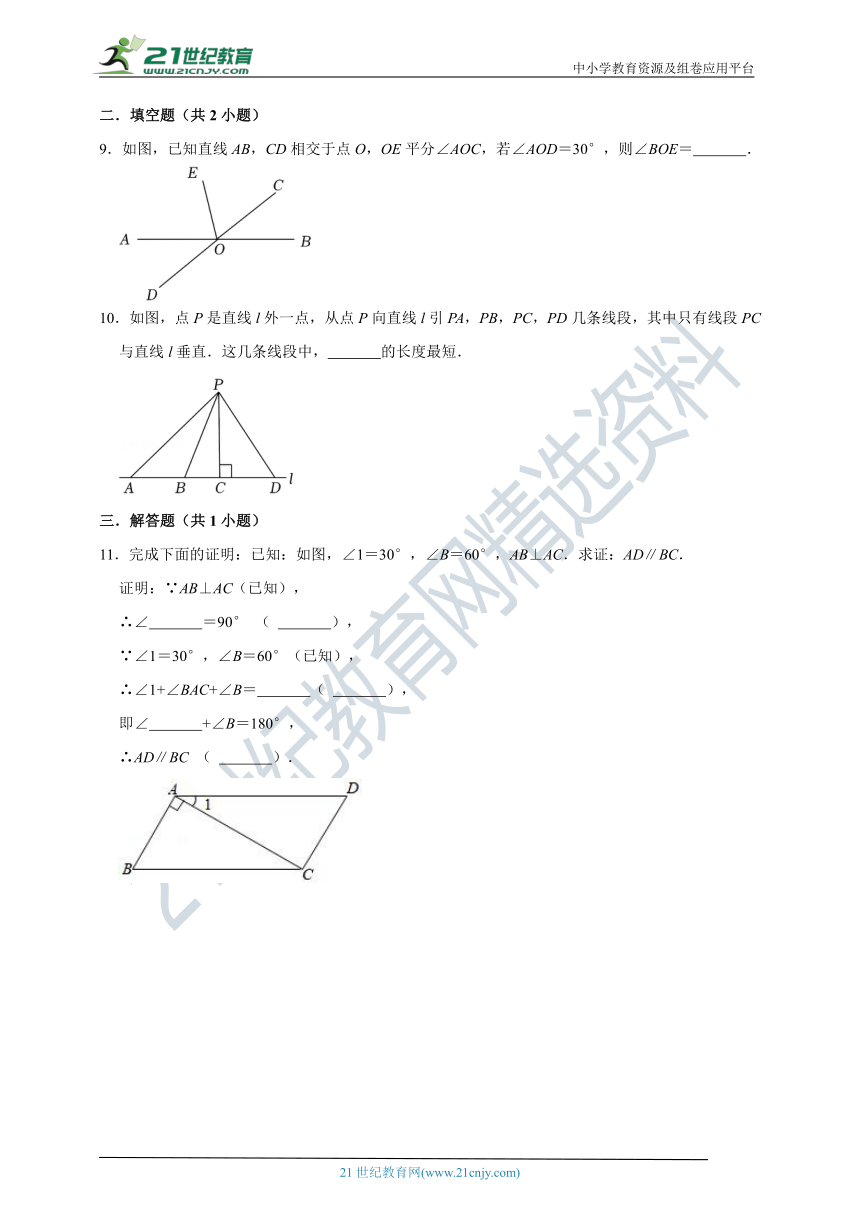
9.如图,已知直线AB,CD相交于点O,OE平分∠AOC,若∠AOD=30°,则∠BOE= .
10.如图,点P是直线l外一点,从点P向直线l引PA,PB,PC,PD几条线段,其中只有线段PC与直线l垂直.这几条线段中, 的长度最短.
三.解答题(共1小题)
11.完成下面的证明:已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.
证明:∵AB⊥AC(已知),
∴∠ =90° ( ),
∵∠1=30°,∠B=60°(已知),
∴∠1+∠BAC+∠B= ( ),
即∠ +∠B=180°,
∴AD∥BC ( ).
参考答案与试题解析
一.选择题(共8小题)
1.如图,直线a、b被直线c所截,下列说法不正确的是( )
A.∠1与∠5是同位角 B.∠2与∠4是对顶角
C.∠3与∠6是同旁内角 D.∠5与∠2是内错角
【解答】解:由图可知:
A.∠1与∠5是同位角,正确,故A不符合题意;
B.∠2与∠4是对顶角,正确,故B不符合题意;
C.∠3与∠6是同旁内角,正确,故C不符合题意;
D.∠5与∠2是内错角,不正确,故D符合题意;
故选:D.
2.如图,AC⊥BC,CD⊥AB,垂足分别为C、D,线段CD的长度是( )
A.点A到BC的距离 B.点B到AC的距离
C.点C到AB的距离 D.点D到AC的距离
【解答】解:∵CD⊥AB,垂足为D,
∴线段CD的长度是点C到AB的距离,
故选:C.
3.如图,直线AB、CD相交于点O,则推导出“∠AOD=∠BOC”,下列依据中,最合理的是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等
【解答】解:∵∠AOD与∠BOC都是∠AOC的补角,
∴∠AOD=∠BOC(同角的补角相等).
故选:C.
4.下列说法正确的是( )
A.不相交的两条直线叫做平行线
B.同一平面内,过一点有且仅有一条直线与已知直线垂直
C.平角是一条直线
D.过同一平面内三点中任意两点,只能画出3条直线
【解答】解:A.应强调在同一平面内,错误;
B.同一平面内,过一点有且仅有一条直线与已知直线垂直,正确;
C.直线与角是不同的两个概念,错误;
D.过同一平面内三点中任意两点,能画出3条直线或1条直线,故错误.
故选:B.
5.如图,不能推出a∥b的条件是( )
A.∠4=∠2 B.∠3+∠4=180° C.∠1=∠3 D.∠2+∠3=180°
【解答】解:∵∠4=∠2,
∴a∥b(内错角相等,两直线平行),故选项A不符合题意;
∠3+∠4=180°,不能得到a∥b,故选项B符合题意;
∵∠1=∠3,
∴a∥b(同位角相等,两直线平行),故选项C不符合题意;
∵∠2+∠3=180°,
∴a∥b(同旁内角互补,两直线平行),故选项D不符合题意;
故选:B.
6.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠3=∠5 B.∠1=∠5 C.∠4+∠5=180° D.∠2=∠4
【解答】解:A.∠3=∠5,可判定a∥b,不符合题意;
B.∠1=∠5,可判定a∥b,不符合题意;
C.∠4+∠5=180°,由同旁内角互补,两直线平行,可判定a∥b,不符合题意;
D.∠2=∠4,不能判定a∥b,符合题意.
故选:D.
7.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
【解答】解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠7+∠4﹣∠1=180°,∠7=∠1+∠3,可得∠3+∠4=180°,即可得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠2=∠3,不能得到a∥b;
故能判断直线a∥b的有5个.
故选:C.
8.如图,下列条件①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC,∠3=∠4;④∠BAD+∠ADC=180°.其中能判定AB∥CD的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①由∠1=∠2可判定AD∥BC,不符合题意;
②由∠BAD=∠BCD不能判定AB∥BC,不符合题意;
③由∠ABC=∠ADC且∠3=∠4知∠ABD=∠CDB,可判定AB∥CD,符合题意;
④由∠BAD+∠ADC=180°可判定AB∥CD,符合题意;
故选:B.
二.填空题(共2小题)
9.如图,已知直线AB,CD相交于点O,OE平分∠AOC,若∠AOD=30°,则∠BOE= 105° .
【解答】解:∵∠AOD=30°,∠AOD=∠BOC,
∴∠AOC=180°﹣∠AOD=150°,∠BOC=30°,
又∵OE平分∠AOC,
∴∠COE=75°,
∴∠B0E=∠COE+∠BOC=75°+30°=105°.
故答案为:105°.
10.如图,点P是直线l外一点,从点P向直线l引PA,PB,PC,PD几条线段,其中只有线段PC与直线l垂直.这几条线段中, PC 的长度最短.
【解答】解:直线外一点P与直线l上各点连接的所有线段中,最短的是PC,依据是垂线段最短,
故答案为:PC.
三.解答题(共1小题)
11.完成下面的证明:已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.
证明:∵AB⊥AC(已知),
∴∠ BAC =90° ( 垂直的定义 ),
∵∠1=30°,∠B=60°(已知),
∴∠1+∠BAC+∠B= 180° ( 等量关系 ),
即∠ BAD +∠B=180°,
∴AD∥BC ( 同旁内角互补,两直线平行 ).
【解答】解:证明:∵AB⊥AC(已知),
∴∠BAC=90° (垂直的定义),
∵∠1=30°,∠B=60°(已知),
∴∠1+∠BAC+∠B=180°(等量关系),
即∠BAD+∠B=180°,
∴AD∥BC (同旁内角互补,两直线平行),
故答案为:BAC;垂直的定义;180°;等量关系;BAD;同旁内角互补,两直线平行.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
相交线与平行线小测
一.选择题(共8小题)
1.如图,直线a、b被直线c所截,下列说法不正确的是( )
A.∠1与∠5是同位角 B.∠2与∠4是对顶角
C.∠3与∠6是同旁内角 D.∠5与∠2是内错角
2.如图,AC⊥BC,CD⊥AB,垂足分别为C、D,线段CD的长度是( )
A.点A到BC的距离 B.点B到AC的距离
C.点C到AB的距离 D.点D到AC的距离
3.如图,直线AB、CD相交于点O,则推导出“∠AOD=∠BOC”,下列依据中,最合理的是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等
4.下列说法正确的是( )
A.不相交的两条直线叫做平行线
B.同一平面内,过一点有且仅有一条直线与已知直线垂直
C.平角是一条直线
D.过同一平面内三点中任意两点,只能画出3条直线
5.如图,不能推出a∥b的条件是( )
A.∠4=∠2 B.∠3+∠4=180° C.∠1=∠3 D.∠2+∠3=180°
6.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠3=∠5 B.∠1=∠5 C.∠4+∠5=180° D.∠2=∠4
7.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
8.如图,下列条件①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC,∠3=∠4;④∠BAD+∠ADC=180°.其中能判定AB∥CD的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共2小题)
9.如图,已知直线AB,CD相交于点O,OE平分∠AOC,若∠AOD=30°,则∠BOE= .
10.如图,点P是直线l外一点,从点P向直线l引PA,PB,PC,PD几条线段,其中只有线段PC与直线l垂直.这几条线段中, 的长度最短.
三.解答题(共1小题)
11.完成下面的证明:已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.
证明:∵AB⊥AC(已知),
∴∠ =90° ( ),
∵∠1=30°,∠B=60°(已知),
∴∠1+∠BAC+∠B= ( ),
即∠ +∠B=180°,
∴AD∥BC ( ).
参考答案与试题解析
一.选择题(共8小题)
1.如图,直线a、b被直线c所截,下列说法不正确的是( )
A.∠1与∠5是同位角 B.∠2与∠4是对顶角
C.∠3与∠6是同旁内角 D.∠5与∠2是内错角
【解答】解:由图可知:
A.∠1与∠5是同位角,正确,故A不符合题意;
B.∠2与∠4是对顶角,正确,故B不符合题意;
C.∠3与∠6是同旁内角,正确,故C不符合题意;
D.∠5与∠2是内错角,不正确,故D符合题意;
故选:D.
2.如图,AC⊥BC,CD⊥AB,垂足分别为C、D,线段CD的长度是( )
A.点A到BC的距离 B.点B到AC的距离
C.点C到AB的距离 D.点D到AC的距离
【解答】解:∵CD⊥AB,垂足为D,
∴线段CD的长度是点C到AB的距离,
故选:C.
3.如图,直线AB、CD相交于点O,则推导出“∠AOD=∠BOC”,下列依据中,最合理的是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等
【解答】解:∵∠AOD与∠BOC都是∠AOC的补角,
∴∠AOD=∠BOC(同角的补角相等).
故选:C.
4.下列说法正确的是( )
A.不相交的两条直线叫做平行线
B.同一平面内,过一点有且仅有一条直线与已知直线垂直
C.平角是一条直线
D.过同一平面内三点中任意两点,只能画出3条直线
【解答】解:A.应强调在同一平面内,错误;
B.同一平面内,过一点有且仅有一条直线与已知直线垂直,正确;
C.直线与角是不同的两个概念,错误;
D.过同一平面内三点中任意两点,能画出3条直线或1条直线,故错误.
故选:B.
5.如图,不能推出a∥b的条件是( )
A.∠4=∠2 B.∠3+∠4=180° C.∠1=∠3 D.∠2+∠3=180°
【解答】解:∵∠4=∠2,
∴a∥b(内错角相等,两直线平行),故选项A不符合题意;
∠3+∠4=180°,不能得到a∥b,故选项B符合题意;
∵∠1=∠3,
∴a∥b(同位角相等,两直线平行),故选项C不符合题意;
∵∠2+∠3=180°,
∴a∥b(同旁内角互补,两直线平行),故选项D不符合题意;
故选:B.
6.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠3=∠5 B.∠1=∠5 C.∠4+∠5=180° D.∠2=∠4
【解答】解:A.∠3=∠5,可判定a∥b,不符合题意;
B.∠1=∠5,可判定a∥b,不符合题意;
C.∠4+∠5=180°,由同旁内角互补,两直线平行,可判定a∥b,不符合题意;
D.∠2=∠4,不能判定a∥b,符合题意.
故选:D.
7.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
【解答】解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠7+∠4﹣∠1=180°,∠7=∠1+∠3,可得∠3+∠4=180°,即可得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠2=∠3,不能得到a∥b;
故能判断直线a∥b的有5个.
故选:C.
8.如图,下列条件①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC,∠3=∠4;④∠BAD+∠ADC=180°.其中能判定AB∥CD的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①由∠1=∠2可判定AD∥BC,不符合题意;
②由∠BAD=∠BCD不能判定AB∥BC,不符合题意;
③由∠ABC=∠ADC且∠3=∠4知∠ABD=∠CDB,可判定AB∥CD,符合题意;
④由∠BAD+∠ADC=180°可判定AB∥CD,符合题意;
故选:B.
二.填空题(共2小题)
9.如图,已知直线AB,CD相交于点O,OE平分∠AOC,若∠AOD=30°,则∠BOE= 105° .
【解答】解:∵∠AOD=30°,∠AOD=∠BOC,
∴∠AOC=180°﹣∠AOD=150°,∠BOC=30°,
又∵OE平分∠AOC,
∴∠COE=75°,
∴∠B0E=∠COE+∠BOC=75°+30°=105°.
故答案为:105°.
10.如图,点P是直线l外一点,从点P向直线l引PA,PB,PC,PD几条线段,其中只有线段PC与直线l垂直.这几条线段中, PC 的长度最短.
【解答】解:直线外一点P与直线l上各点连接的所有线段中,最短的是PC,依据是垂线段最短,
故答案为:PC.
三.解答题(共1小题)
11.完成下面的证明:已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.
证明:∵AB⊥AC(已知),
∴∠ BAC =90° ( 垂直的定义 ),
∵∠1=30°,∠B=60°(已知),
∴∠1+∠BAC+∠B= 180° ( 等量关系 ),
即∠ BAD +∠B=180°,
∴AD∥BC ( 同旁内角互补,两直线平行 ).
【解答】解:证明:∵AB⊥AC(已知),
∴∠BAC=90° (垂直的定义),
∵∠1=30°,∠B=60°(已知),
∴∠1+∠BAC+∠B=180°(等量关系),
即∠BAD+∠B=180°,
∴AD∥BC (同旁内角互补,两直线平行),
故答案为:BAC;垂直的定义;180°;等量关系;BAD;同旁内角互补,两直线平行.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
