2020-2021学年湖北省武汉市华师一附中光谷校区九年级下开学考数学试卷(图片版含答案)
文档属性
| 名称 | 2020-2021学年湖北省武汉市华师一附中光谷校区九年级下开学考数学试卷(图片版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览




文档简介
∴抛物线的解析式为y=-x2-2x+4
(2)如图1,设P(,-212t+4,过点P作PE∥y轴交AB与点E,设直线AB的解析式为y=kx+
b,把A(-3,1,(0,4)代入得到,{。54解得=1
3k+b=1
b=4
直线AB的解析式为y=x+4,
∵E(t,t+4),
PE=-t2-2t+4-(t+4)=-t2-3t
1
.SAP4BsS△pEA+S△PBE一2
PE×3
2(2+31)=-2(t+3)+
27
8
当t=-3时,S△PBA有最大值
点
319
(3)由y=-x2+kx-2k=k(x-2)-x2,当x-2=0时,x=2,y=-4
无论k取何值,拋物线都经过定点H(2,-4),
二次函数的顶点N(,4-2k)
①如图2中,若点N在ⅹ轴下方时,过点H作HE⊥X轴于E,过N作NF⊥HE于点F,
M(2,0),H(2,-4),
∴ME=4,HE=4
∠MHE=45
∴∠MHN=90
∠NHF=900-45°=45°,
∴FN=FH∴
4-2k-(-4)=k
k2-10k+24=0
M-2,0)
E
k=6或k=4当k=4时,
k
2=24-2k
4,
N(2,-4)与H重合
H(2-4)
k=4(不合题意舍弃)
抢物线的解析式为y=-x2+6x-12
②如图3中若点N在x轴上方时过点H作HE⊥X轴于E,过N作NF⊥x轴于点F
同理可得,∠NMF=45°,
∴NF=FM
4~2kk
M-2
即k2-10k=8
解得k=5+√33,或k=5-√33
抛物线的解析式为y=-x2+(5+√33)x-10-2√33
或y=-x2+(5-√33)x-10+2√33
综上所述,抛物线的解析式为y=-x2+6x-12,y=-x2+(5+√33)x-10-233或y=
-x2+(5-√33)x-10+2√33
华中师大一附中光谷分校2020-2021学年度第二学期九年级开学测试卷
、选择题(共6小题,每小题3分,共18分)
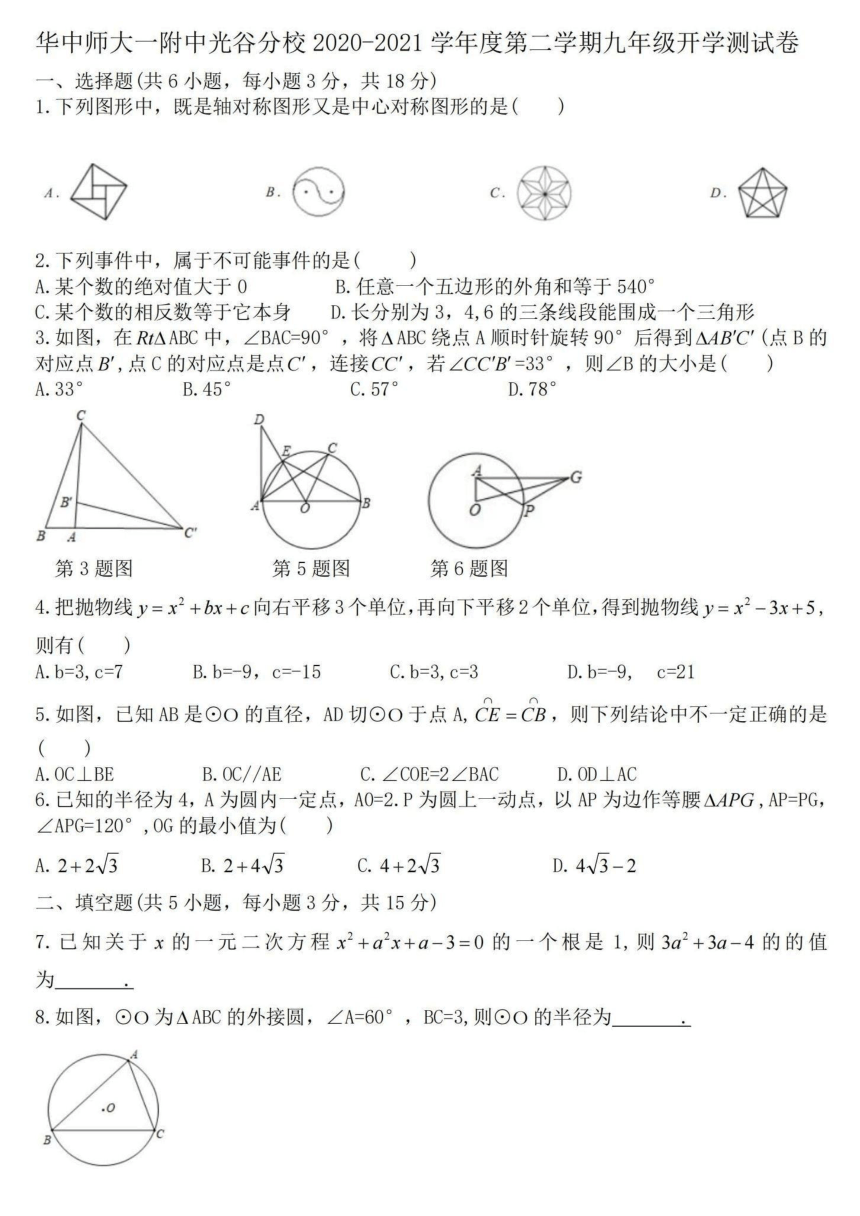
1.下列图形中,既是轴对称图形又是中心对称图形的是()
B
C
2.下列事件中,属于不可能事件的是()
A.某个数的绝对值大于0
B.任意一个五边形的外角和等于540°
C.某个数的相反数等于它本身D.长分别为3,4,6的三条线段能围成一个三角形
3.如图,在 RtAABC中,∠BAC=90°,将ΔABC绕点A顺时针旋转90°后得到△ABC'(点B的
对应点B′,点C的对应点是点C′,连接CC′,若∠CCB′=33°,则∠B的大小是()
A.33°
B.45°
C.57°
D.78°
B
B
第3题图
第5题图
第6题图
4.把抛物线y=x2+bx+c向右平移3个单位,再向下平移2个单位,得到抛物线y=x2-3x+5,
则有()
A.b=3,c=7
B.b=-9,c=-15
C.b=3,c=3
D.b=-9,c=21
5.如图,已知AB是⊙O的直径,AD切⊙O于点A,CE=CB,则下列结论中不一定正确的是
A.0C⊥BE
B OC//AE
C.∠COE=2∠BAC
D.OD⊥AC
6.已知的半径为4,A为圆内一定点,A0=2.P为圆上一动点,以AP为边作等腰△APG,AP=PG,
∠APG=120°,0G的最小值为(
A.2+2√3
B.2+4√3
C.4+2√3
D.4√3-2
、填空题(共5小题,每小题3分,共15分)
7.已知关于x的一元二次方程x2+a2x+a-3=0的一个根是1,则3a2+3a-4的的值
为
8.如图,⊙O为△ABC的外接圆,∠A=60°,BC=3,则⊙O的半径为
(2)如图1,设P(,-212t+4,过点P作PE∥y轴交AB与点E,设直线AB的解析式为y=kx+
b,把A(-3,1,(0,4)代入得到,{。54解得=1
3k+b=1
b=4
直线AB的解析式为y=x+4,
∵E(t,t+4),
PE=-t2-2t+4-(t+4)=-t2-3t
1
.SAP4BsS△pEA+S△PBE一2
PE×3
2(2+31)=-2(t+3)+
27
8
当t=-3时,S△PBA有最大值
点
319
(3)由y=-x2+kx-2k=k(x-2)-x2,当x-2=0时,x=2,y=-4
无论k取何值,拋物线都经过定点H(2,-4),
二次函数的顶点N(,4-2k)
①如图2中,若点N在ⅹ轴下方时,过点H作HE⊥X轴于E,过N作NF⊥HE于点F,
M(2,0),H(2,-4),
∴ME=4,HE=4
∠MHE=45
∴∠MHN=90
∠NHF=900-45°=45°,
∴FN=FH∴
4-2k-(-4)=k
k2-10k+24=0
M-2,0)
E
k=6或k=4当k=4时,
k
2=24-2k
4,
N(2,-4)与H重合
H(2-4)
k=4(不合题意舍弃)
抢物线的解析式为y=-x2+6x-12
②如图3中若点N在x轴上方时过点H作HE⊥X轴于E,过N作NF⊥x轴于点F
同理可得,∠NMF=45°,
∴NF=FM
4~2kk
M-2
即k2-10k=8
解得k=5+√33,或k=5-√33
抛物线的解析式为y=-x2+(5+√33)x-10-2√33
或y=-x2+(5-√33)x-10+2√33
综上所述,抛物线的解析式为y=-x2+6x-12,y=-x2+(5+√33)x-10-233或y=
-x2+(5-√33)x-10+2√33
华中师大一附中光谷分校2020-2021学年度第二学期九年级开学测试卷
、选择题(共6小题,每小题3分,共18分)
1.下列图形中,既是轴对称图形又是中心对称图形的是()
B
C
2.下列事件中,属于不可能事件的是()
A.某个数的绝对值大于0
B.任意一个五边形的外角和等于540°
C.某个数的相反数等于它本身D.长分别为3,4,6的三条线段能围成一个三角形
3.如图,在 RtAABC中,∠BAC=90°,将ΔABC绕点A顺时针旋转90°后得到△ABC'(点B的
对应点B′,点C的对应点是点C′,连接CC′,若∠CCB′=33°,则∠B的大小是()
A.33°
B.45°
C.57°
D.78°
B
B
第3题图
第5题图
第6题图
4.把抛物线y=x2+bx+c向右平移3个单位,再向下平移2个单位,得到抛物线y=x2-3x+5,
则有()
A.b=3,c=7
B.b=-9,c=-15
C.b=3,c=3
D.b=-9,c=21
5.如图,已知AB是⊙O的直径,AD切⊙O于点A,CE=CB,则下列结论中不一定正确的是
A.0C⊥BE
B OC//AE
C.∠COE=2∠BAC
D.OD⊥AC
6.已知的半径为4,A为圆内一定点,A0=2.P为圆上一动点,以AP为边作等腰△APG,AP=PG,
∠APG=120°,0G的最小值为(
A.2+2√3
B.2+4√3
C.4+2√3
D.4√3-2
、填空题(共5小题,每小题3分,共15分)
7.已知关于x的一元二次方程x2+a2x+a-3=0的一个根是1,则3a2+3a-4的的值
为
8.如图,⊙O为△ABC的外接圆,∠A=60°,BC=3,则⊙O的半径为
同课章节目录
