【人教版】数学八年级下册 第17章 专题训练(二)折叠与展开邂逅勾股定理 习题课件
文档属性
| 名称 | 【人教版】数学八年级下册 第17章 专题训练(二)折叠与展开邂逅勾股定理 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 09:37:52 | ||
图片预览




文档简介
(共14张PPT)
第十七章 勾股定理
专题训练(二)
折叠与展 开邂逅勾股定理
D
A
B
A
D
B
D
1
4
5
A2
C2
C1
A2
1
C1
4
5
A2
4
D2
5
1
C1
专题(三)
勾股定理牵手图形面积与分类思想
D
C
B
D
128
4
9或21
①
A
②
D
D
E
E
①
②
下页
上页
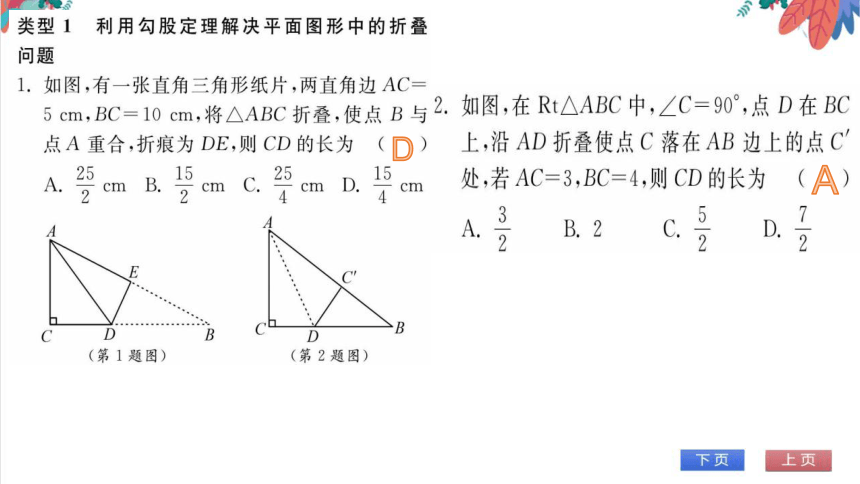
类型1利用勾股定理解决平面图形中的折叠
问题
如图,有一张直角三角形纸片,两直角边AC
5cm,BC=10cm,将△ABC折叠,使点B与
点A重合,折痕为DE,则CD的长为()
2 cm B 15
25
cm
cm
4
(第1题图
第2题图
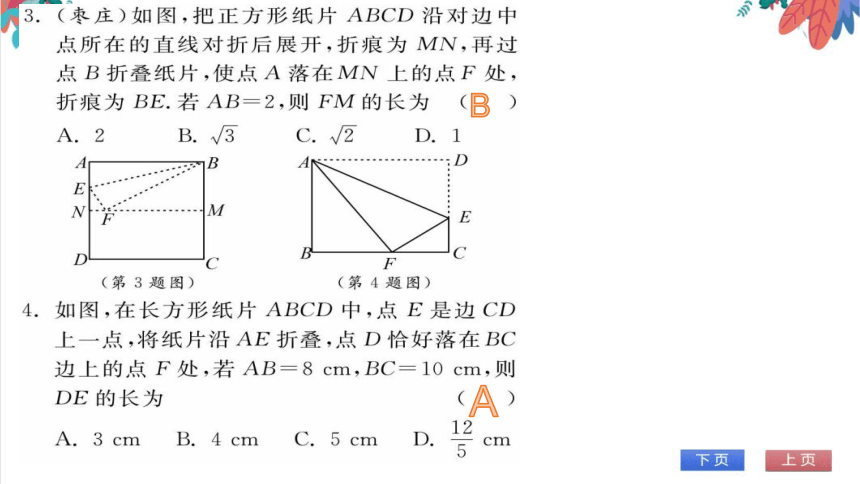
3.(枣庄)如图,把正方形纸片ABCD沿对边中
点所在的直线对折后展开,折痕为MN,再过
点B折叠纸片,使点A落在MN上的点F处,
折痕为BE.若AB=2,则FM的长为(
A.2
B.√3
C.√2
B
D
E
(第3题图)
(第4题图)
5.如图,在平面直角坐标系中,A(3,0),B(0,4),
连接AB,将线段AB沿过点A的直线翻折,
使点B仍然落在x轴上,折痕交y轴于点C,
则点C的坐标为
类型2利用勾股定理解决立体图形中的展开
问题
6.(东营)如图,点B为正方体棱的中点,一只蚂
蚁沿边长为2的正方体表面从A点出发,到
达B点,则它运动的最短路径为
A.√5
B.2√2C.√7D.√17
B
A
A
B
C
(第6题图)
(第7题图)(第8题图)
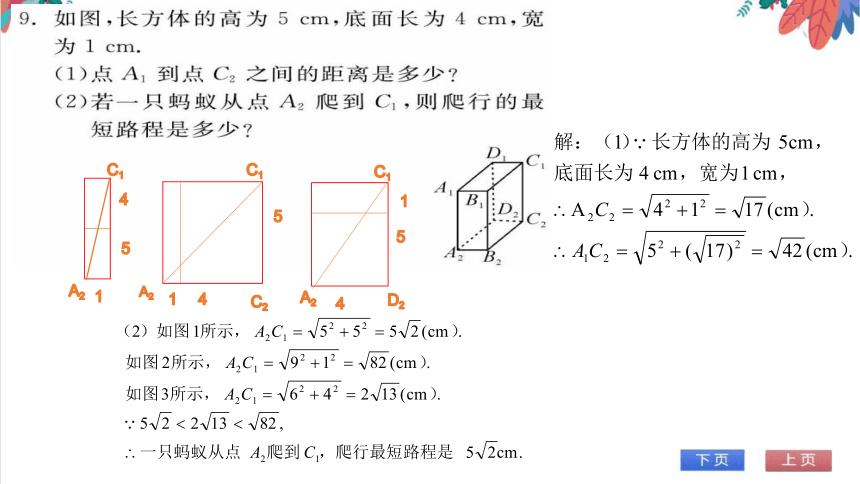
9.如图,长方体的高为5cm,底面长为4cm,宽
为1cm.
(1)点A1到点C2之间的距离是多少
(2)若一只蚂蚁从点A2爬到C1,则爬行的最
短路程是多少
类型1利用勾股定理解决图形面积问题
1.已知在Rt△ABC中,∠C=90°,若a+b=
12cm,c=10cm,则Rt△ABC的面积是()
A. 48 cm
B. 24 cm2
C. 16 cm2
D. 11 cm2
2.(襄阳)“赵爽弦图”巧妙地利用面积关系证明
了勾股定理,是我国古代数学的骄傲.如图所
示的“赵爽弦图”是由四个全等的直角三角形
和一个小正方形拼成的大正方形.设直角三角
形较长直角边长为a,较短直角边长为b.若
(a+b)2=21,大正方形的面积为13,则小正方
形的面积为
A.3
B.4
C.5
D.6
E
(第2题图)
(第3题图)
3.(莆田)如图是一株美丽的勾股树,其中所有的
四边形都是正方形,所有的三角形都是直角三
角形,若正方形A,B,C,D的边长分别是3,5,
2,3,则最大正方形E的面积是
A.94
B.47
C.26
D.13
第十七章 勾股定理
专题训练(二)
折叠与展 开邂逅勾股定理
D
A
B
A
D
B
D
1
4
5
A2
C2
C1
A2
1
C1
4
5
A2
4
D2
5
1
C1
专题(三)
勾股定理牵手图形面积与分类思想
D
C
B
D
128
4
9或21
①
A
②
D
D
E
E
①
②
下页
上页
类型1利用勾股定理解决平面图形中的折叠
问题
如图,有一张直角三角形纸片,两直角边AC
5cm,BC=10cm,将△ABC折叠,使点B与
点A重合,折痕为DE,则CD的长为()
2 cm B 15
25
cm
cm
4
(第1题图
第2题图
3.(枣庄)如图,把正方形纸片ABCD沿对边中
点所在的直线对折后展开,折痕为MN,再过
点B折叠纸片,使点A落在MN上的点F处,
折痕为BE.若AB=2,则FM的长为(
A.2
B.√3
C.√2
B
D
E
(第3题图)
(第4题图)
5.如图,在平面直角坐标系中,A(3,0),B(0,4),
连接AB,将线段AB沿过点A的直线翻折,
使点B仍然落在x轴上,折痕交y轴于点C,
则点C的坐标为
类型2利用勾股定理解决立体图形中的展开
问题
6.(东营)如图,点B为正方体棱的中点,一只蚂
蚁沿边长为2的正方体表面从A点出发,到
达B点,则它运动的最短路径为
A.√5
B.2√2C.√7D.√17
B
A
A
B
C
(第6题图)
(第7题图)(第8题图)
9.如图,长方体的高为5cm,底面长为4cm,宽
为1cm.
(1)点A1到点C2之间的距离是多少
(2)若一只蚂蚁从点A2爬到C1,则爬行的最
短路程是多少
类型1利用勾股定理解决图形面积问题
1.已知在Rt△ABC中,∠C=90°,若a+b=
12cm,c=10cm,则Rt△ABC的面积是()
A. 48 cm
B. 24 cm2
C. 16 cm2
D. 11 cm2
2.(襄阳)“赵爽弦图”巧妙地利用面积关系证明
了勾股定理,是我国古代数学的骄傲.如图所
示的“赵爽弦图”是由四个全等的直角三角形
和一个小正方形拼成的大正方形.设直角三角
形较长直角边长为a,较短直角边长为b.若
(a+b)2=21,大正方形的面积为13,则小正方
形的面积为
A.3
B.4
C.5
D.6
E
(第2题图)
(第3题图)
3.(莆田)如图是一株美丽的勾股树,其中所有的
四边形都是正方形,所有的三角形都是直角三
角形,若正方形A,B,C,D的边长分别是3,5,
2,3,则最大正方形E的面积是
A.94
B.47
C.26
D.13
