【人教版】数学八年级下册 第18章 重难点突破 习题课件
文档属性
| 名称 | 【人教版】数学八年级下册 第18章 重难点突破 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 09:37:52 | ||
图片预览



文档简介
(共17张PPT)
本章重难点突破
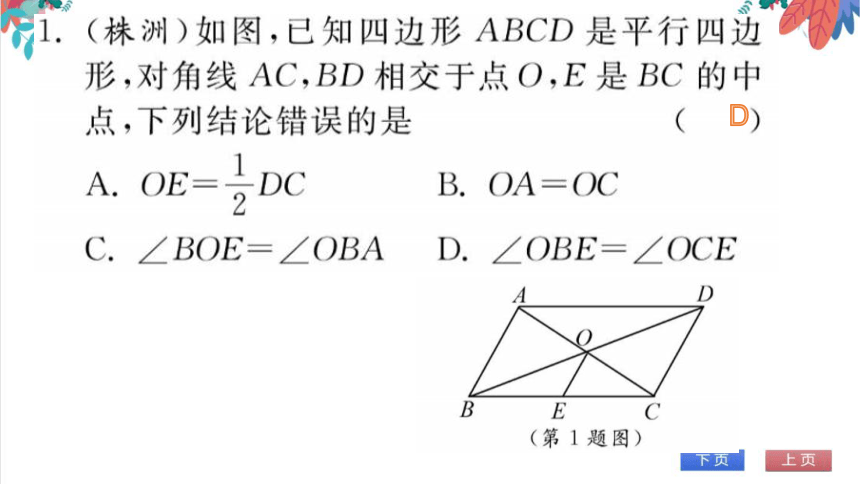
D
D
1.5
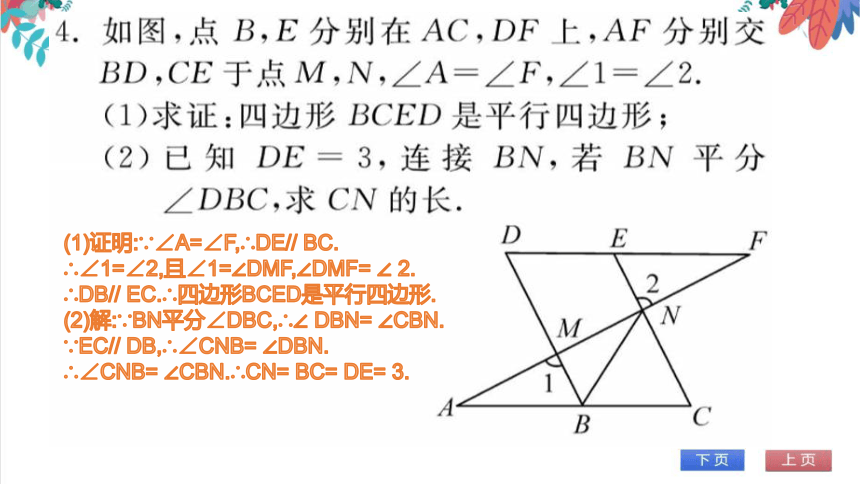
(1)证明:∵∠A=∠F,∴DE// BC.
∴∠1=∠2,且∠1=∠DMF,∠DMF= ∠ 2.
∴DB// EC.∴四边形BCED是平行四边形.
(2)解:∵BN平分∠DBC,∴∠ DBN= ∠CBN.
∵EC// DB,∴∠CNB= ∠DBN.
∴∠CNB= ∠CBN.∴CN= BC= DE= 3.
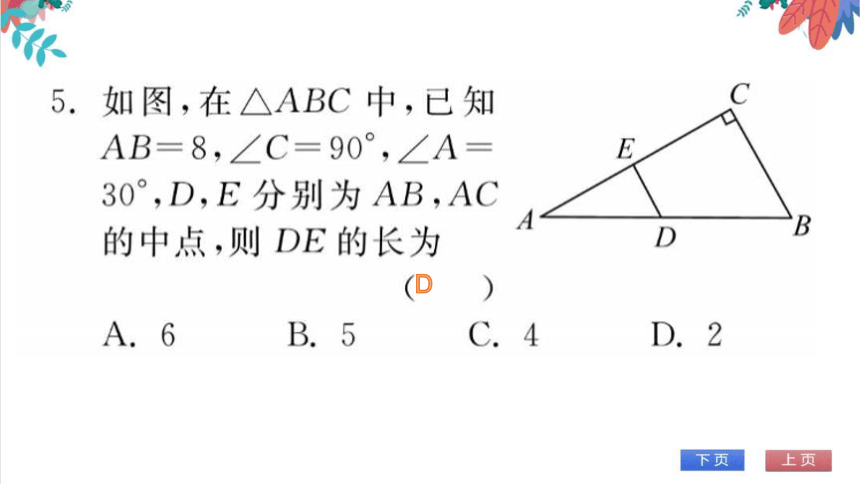
D
B
A
4√3或2√3
(3,√3)
证明:∵四边形ABCD是平行四边形,
∴AD//BC,CD//AB.∴∠CDB=∠ABD.
∵BE平分∠ABD,DF平分∠CDB,
∴∠FDB=1/2∠CDB,∠ EBD=1/2 ∠ABD.
∴∠FDB=∠EBD. .DF// EB.
又∵AD// BC.∴四边形DFBE是平行四边形.
∵AB=DB,BE平分∠ ABD,
∴BE⊥AD.∴∠DEB= 90°.
∴四边形DFBE是矩形.
解:(1)A=-CG-CE.证明:∵四边形ABCD是菱形.∴AB=BC.
又∵∠BAC=60°,∴ ABC是等边三角形。
∴∠ABC=∠ACB=∠BAC=60°,AB=AC.∵ AD// BC,AB//DC.
∴∠DAC=∠ACB=∠BAC=∠ACD=∠EAG= 60°.
∴∠BAC+∠CAE= ∠ EAG+∠CAE, 即∠BAE∠CAG.
在 ABE和 ACG中,
∠BAE=∠CAG,AB=AC,∠ABC=∠ACD,
∴ ABE≌ ACG(ASA).∴BE=CG.
∵ BC=CD,∴CE= DG.
∵ AB=CD=CG- DG,.AB= CG- CE.
(2)AB=CE- CG.
C
(1)证明:∵在Rt OAB中,D为OB的中点,∴DO=DA.∴∠DAO=∠DOA= 30°,可求∠EOA = 90°,
∴∠AEO=60°.又:∵ OBC为等边三角形,∴∠BCO=∠AE0=60°. .∴BC//AE. ∵∠BAO=∠COA= 90°,
∴CO//AB. ∴四边形ABCE是平行四边形,
(2)解:设OG=x,由折叠可得AG=GC=8-x,在Rt ABO中,∴∠OAB= 90°,∠AOB= 30°,BO= 8,
∴AB=4.∴ AO=4√3,在Rt △OAG中,OG + OA =AG ,即x +(4√3) =(8-x) ,解得x=1.∴0G=1.
本章重难点突破
D
D
1.5
(1)证明:∵∠A=∠F,∴DE// BC.
∴∠1=∠2,且∠1=∠DMF,∠DMF= ∠ 2.
∴DB// EC.∴四边形BCED是平行四边形.
(2)解:∵BN平分∠DBC,∴∠ DBN= ∠CBN.
∵EC// DB,∴∠CNB= ∠DBN.
∴∠CNB= ∠CBN.∴CN= BC= DE= 3.
D
B
A
4√3或2√3
(3,√3)
证明:∵四边形ABCD是平行四边形,
∴AD//BC,CD//AB.∴∠CDB=∠ABD.
∵BE平分∠ABD,DF平分∠CDB,
∴∠FDB=1/2∠CDB,∠ EBD=1/2 ∠ABD.
∴∠FDB=∠EBD. .DF// EB.
又∵AD// BC.∴四边形DFBE是平行四边形.
∵AB=DB,BE平分∠ ABD,
∴BE⊥AD.∴∠DEB= 90°.
∴四边形DFBE是矩形.
解:(1)A=-CG-CE.证明:∵四边形ABCD是菱形.∴AB=BC.
又∵∠BAC=60°,∴ ABC是等边三角形。
∴∠ABC=∠ACB=∠BAC=60°,AB=AC.∵ AD// BC,AB//DC.
∴∠DAC=∠ACB=∠BAC=∠ACD=∠EAG= 60°.
∴∠BAC+∠CAE= ∠ EAG+∠CAE, 即∠BAE∠CAG.
在 ABE和 ACG中,
∠BAE=∠CAG,AB=AC,∠ABC=∠ACD,
∴ ABE≌ ACG(ASA).∴BE=CG.
∵ BC=CD,∴CE= DG.
∵ AB=CD=CG- DG,.AB= CG- CE.
(2)AB=CE- CG.
C
(1)证明:∵在Rt OAB中,D为OB的中点,∴DO=DA.∴∠DAO=∠DOA= 30°,可求∠EOA = 90°,
∴∠AEO=60°.又:∵ OBC为等边三角形,∴∠BCO=∠AE0=60°. .∴BC//AE. ∵∠BAO=∠COA= 90°,
∴CO//AB. ∴四边形ABCE是平行四边形,
(2)解:设OG=x,由折叠可得AG=GC=8-x,在Rt ABO中,∴∠OAB= 90°,∠AOB= 30°,BO= 8,
∴AB=4.∴ AO=4√3,在Rt △OAG中,OG + OA =AG ,即x +(4√3) =(8-x) ,解得x=1.∴0G=1.
