【人教版】数学八年级下册 第19章 专题训练(七)利用图象解决应用题 习题课件
文档属性
| 名称 | 【人教版】数学八年级下册 第19章 专题训练(七)利用图象解决应用题 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 09:37:52 | ||
图片预览




文档简介
(共10张PPT)
第十九章
专题训练(七)利用图象解决应用题
C
80
下页
上页
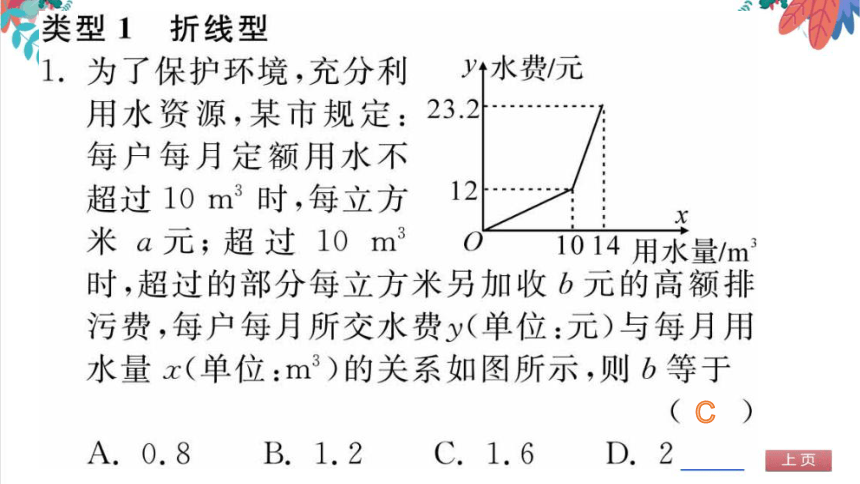
类型1折线型
为了保护环境,充分利水费元
用水资源,某市规定:23.2
每户每月定额用水不
超过10m3时,每立方
米a元;超过10mO1014用水量/m3
时,超过的部分每立方米另加收b元的高额排
污费,每户每月所交水费y(单位:元)与每月用
水量x(单位:m3)的关系如图所示,则b等于
A.0.8B.1.2C.1.6D.2
2.(淮安)甲、乙两地的路程为290km,一辆汽车
早上8:00从甲地出发,匀速向乙地行驶,途中
休息一段时间后,按原速继续前进,当离甲地
路程为240km时接到通知,要求中午12:00
准时到达乙地.设汽车出发xh后离甲地的路
程为ykm,图中折线OCDE表示接到通知前
y与x之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度为
km/h
(2)求线段DE所表示的y与x之间的函数解
析式;
解:(2)休息后按原速继续前进行
驶的时间为(240-80)÷80=2
(h),2+1.5=3.5(h).
点E的坐标为(3.5,240)
设线段DE所表示的y与x之间
的函数解析式为y=kx+b,则:
1.5k+b=80,解得(b=-40
k=80,
3.5k+b=240.
类型2双线型
(上海)某物流公司引进A,B两种机器人用来
搬运某种货物,这两种机器人充满电后可以连
续搬运5h,A种机器人于某日0时开始搬运,
过了1h,B种机器人也开始搬运.如图所示,
线段OG表示A种机器人的搬运量yA(单
位:kg)与时间x(单位:h)的函数图象,线段
EF表示B种机器人的搬运量y(单位:kg)与
时间x(单位:h)的函数图象.根据图象提供的
信息,解答下列问题
(1)求yB关于x的函数解析式;
解:(1)设yB关于x的函数解
y/kg
yBF
析式为yB=kx+b(k≠0)
将点(1,0),(3,180)代入得
k+b=0,
k=90,
180-…
解得
3k+b=180,
b=-90
所以y关于x的函数解析式
E
x/h
为yB=90x-90(1≤x≤6)
(2)设M关于x的解析式为y=kx
根据题意得3k1=180,解得k1=60
所以y=60x(0≤x≤5)
当x=5时,yA=60×5=300(kg)
当x=6时,yB=90×6-90=450(kg)
50-300=150(kg)
答:如果A,B两种机器人各连续搬运5h,B种机器人比
A种机器人多搬运了150kg
第十九章
专题训练(七)利用图象解决应用题
C
80
下页
上页
类型1折线型
为了保护环境,充分利水费元
用水资源,某市规定:23.2
每户每月定额用水不
超过10m3时,每立方
米a元;超过10mO1014用水量/m3
时,超过的部分每立方米另加收b元的高额排
污费,每户每月所交水费y(单位:元)与每月用
水量x(单位:m3)的关系如图所示,则b等于
A.0.8B.1.2C.1.6D.2
2.(淮安)甲、乙两地的路程为290km,一辆汽车
早上8:00从甲地出发,匀速向乙地行驶,途中
休息一段时间后,按原速继续前进,当离甲地
路程为240km时接到通知,要求中午12:00
准时到达乙地.设汽车出发xh后离甲地的路
程为ykm,图中折线OCDE表示接到通知前
y与x之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度为
km/h
(2)求线段DE所表示的y与x之间的函数解
析式;
解:(2)休息后按原速继续前进行
驶的时间为(240-80)÷80=2
(h),2+1.5=3.5(h).
点E的坐标为(3.5,240)
设线段DE所表示的y与x之间
的函数解析式为y=kx+b,则:
1.5k+b=80,解得(b=-40
k=80,
3.5k+b=240.
类型2双线型
(上海)某物流公司引进A,B两种机器人用来
搬运某种货物,这两种机器人充满电后可以连
续搬运5h,A种机器人于某日0时开始搬运,
过了1h,B种机器人也开始搬运.如图所示,
线段OG表示A种机器人的搬运量yA(单
位:kg)与时间x(单位:h)的函数图象,线段
EF表示B种机器人的搬运量y(单位:kg)与
时间x(单位:h)的函数图象.根据图象提供的
信息,解答下列问题
(1)求yB关于x的函数解析式;
解:(1)设yB关于x的函数解
y/kg
yBF
析式为yB=kx+b(k≠0)
将点(1,0),(3,180)代入得
k+b=0,
k=90,
180-…
解得
3k+b=180,
b=-90
所以y关于x的函数解析式
E
x/h
为yB=90x-90(1≤x≤6)
(2)设M关于x的解析式为y=kx
根据题意得3k1=180,解得k1=60
所以y=60x(0≤x≤5)
当x=5时,yA=60×5=300(kg)
当x=6时,yB=90×6-90=450(kg)
50-300=150(kg)
答:如果A,B两种机器人各连续搬运5h,B种机器人比
A种机器人多搬运了150kg
