【人教版】数学八年级下册 17.1 勾股定理 习题课件
文档属性
| 名称 | 【人教版】数学八年级下册 17.1 勾股定理 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
A
B
C
勾股定理
a2+b2=c2
C
C
C
A
12
30
B
C
C
A
49
13
①
②
第2课时 勾股定理的应用
C
A
C
A
B
B
D
D
C
A
B
C
D
D
①
②
③
下页
上页
知识要点全练∥分奥基
知识点1勾股定理的认识
1.(滨州)在直角三角形中,若勾为3,股为4,则
弦为
A.5
B.6
D.8
2.如图,在边长为1个单位长度的小A
正方形网格中,点A,B都是格点
(即网格线的交点),则线段AB的
B
长度为
A.3√3B.5
D.4√2
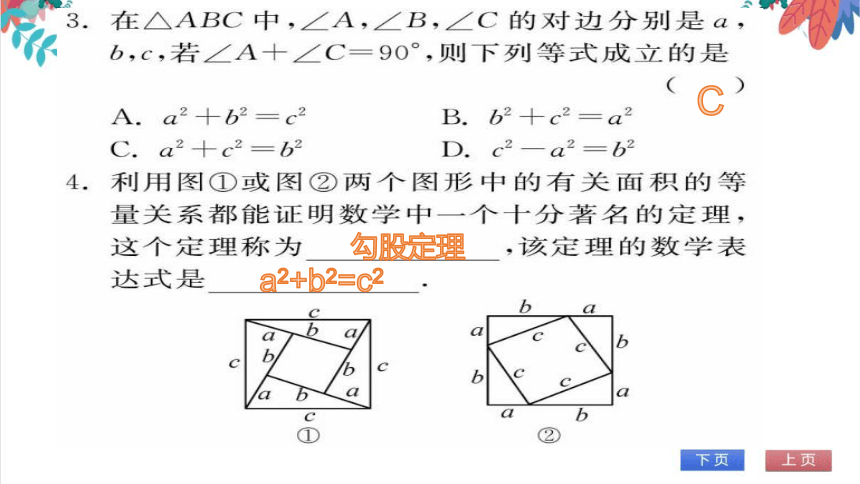
3.在△ABC中,∠A,∠B,∠C的对边分别是a,
b,c,若∠A+∠C=90°,则下列等式成立的是
A.a2+b2=c2
B.b2+c2=a2
C.a2+c2=b2
D
4.利用图①或图②两个图形中的有关面积的等
量关系都能证明数学中一个十分著名的定理,
这个定理称为
,该定理的数学表
达式是
如图是美国总统 Garfield于1896年给出的
种验证勾股定理的办法,你能利用它证明勾股
定理吗 请你写出证明过程(提示:图中三个
三角形均是直角三角形)
知识点2勾股定理的简单应用
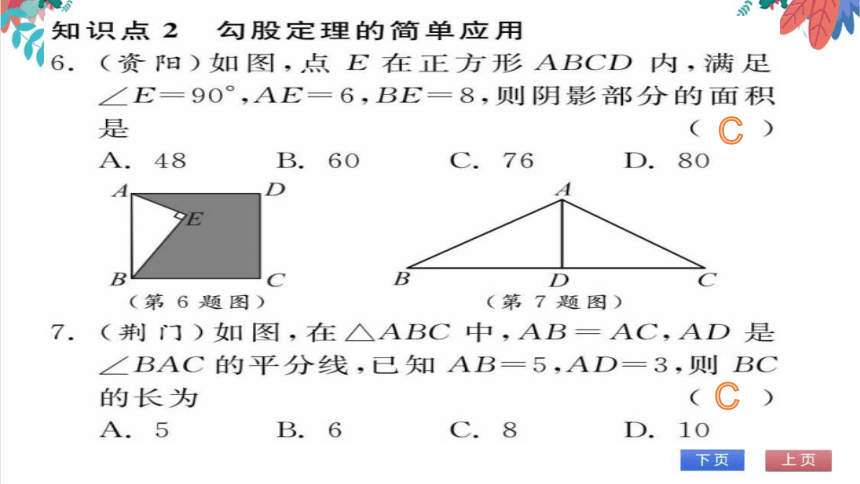
6.(资阳)如图,点E在正方形ABCD内,满足
∠E=90°,AE=6,BE=8,则阴影部分的面积
是
A.48
B.60
C.76
D.80
B
C
D
(第6题图)
(第7题图)
7.(荆门)如图,在△ABC中,AB=AC,AD是
∠BAC的平分线,已知AB=5,AD=3,则BC
的长为
A.5
B.6
D.10
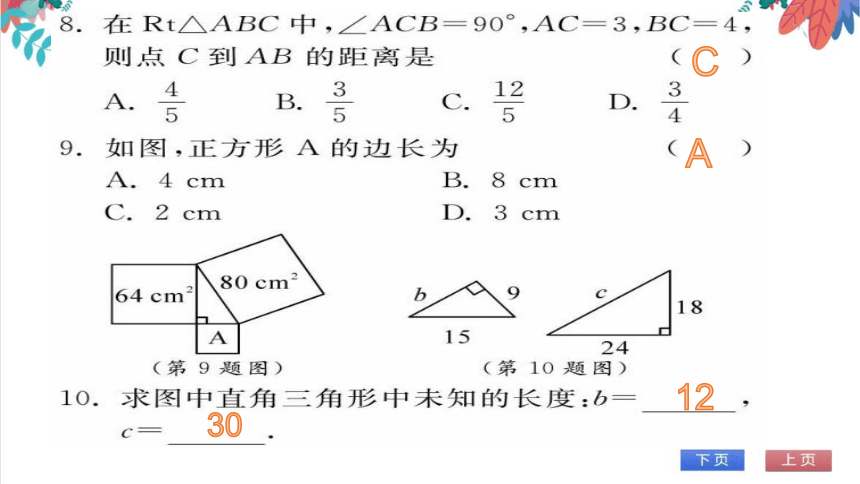
8.在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
则点C到AB的距离是
12
4
9.如图,正方形A的边长为
A.4
cm
B.8 cm
cm
cm
80 cm
64 cm
4
(第9题图)
(第10题图)
10.求图中直角三角形中未知的长度:b=
C
11.已知某直角三角形的两条直角边的长分别为
52和12√2,则这个直角三角形的周长为
12.在△ABC中,∠C=90°,AB=c,BC=a,
Ac-b
(1)若a=7,b=24,求c;
(2)若c=√51,b=√2,求a
规律方法全练
提升能力
13.等腰三角形的底边长为6,底边上的中线长
为4,则它的腰长为
A.4
B.5
14.在Rt△ABC中,AB=3,AC=4,则BC的
长为
B.√7
C.5或√7
D.无法确定
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
A
B
C
勾股定理
a2+b2=c2
C
C
C
A
12
30
B
C
C
A
49
13
①
②
第2课时 勾股定理的应用
C
A
C
A
B
B
D
D
C
A
B
C
D
D
①
②
③
下页
上页
知识要点全练∥分奥基
知识点1勾股定理的认识
1.(滨州)在直角三角形中,若勾为3,股为4,则
弦为
A.5
B.6
D.8
2.如图,在边长为1个单位长度的小A
正方形网格中,点A,B都是格点
(即网格线的交点),则线段AB的
B
长度为
A.3√3B.5
D.4√2
3.在△ABC中,∠A,∠B,∠C的对边分别是a,
b,c,若∠A+∠C=90°,则下列等式成立的是
A.a2+b2=c2
B.b2+c2=a2
C.a2+c2=b2
D
4.利用图①或图②两个图形中的有关面积的等
量关系都能证明数学中一个十分著名的定理,
这个定理称为
,该定理的数学表
达式是
如图是美国总统 Garfield于1896年给出的
种验证勾股定理的办法,你能利用它证明勾股
定理吗 请你写出证明过程(提示:图中三个
三角形均是直角三角形)
知识点2勾股定理的简单应用
6.(资阳)如图,点E在正方形ABCD内,满足
∠E=90°,AE=6,BE=8,则阴影部分的面积
是
A.48
B.60
C.76
D.80
B
C
D
(第6题图)
(第7题图)
7.(荆门)如图,在△ABC中,AB=AC,AD是
∠BAC的平分线,已知AB=5,AD=3,则BC
的长为
A.5
B.6
D.10
8.在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
则点C到AB的距离是
12
4
9.如图,正方形A的边长为
A.4
cm
B.8 cm
cm
cm
80 cm
64 cm
4
(第9题图)
(第10题图)
10.求图中直角三角形中未知的长度:b=
C
11.已知某直角三角形的两条直角边的长分别为
52和12√2,则这个直角三角形的周长为
12.在△ABC中,∠C=90°,AB=c,BC=a,
Ac-b
(1)若a=7,b=24,求c;
(2)若c=√51,b=√2,求a
规律方法全练
提升能力
13.等腰三角形的底边长为6,底边上的中线长
为4,则它的腰长为
A.4
B.5
14.在Rt△ABC中,AB=3,AC=4,则BC的
长为
B.√7
C.5或√7
D.无法确定
