【人教版】数学八年级下册 第18章 专题训练(四)判定正方形两捷径 习题课件
文档属性
| 名称 | 【人教版】数学八年级下册 第18章 专题训练(四)判定正方形两捷径 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 812.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 09:37:52 | ||
图片预览

文档简介
(共7张PPT)
专题训练(四)
判定正方形两捷径
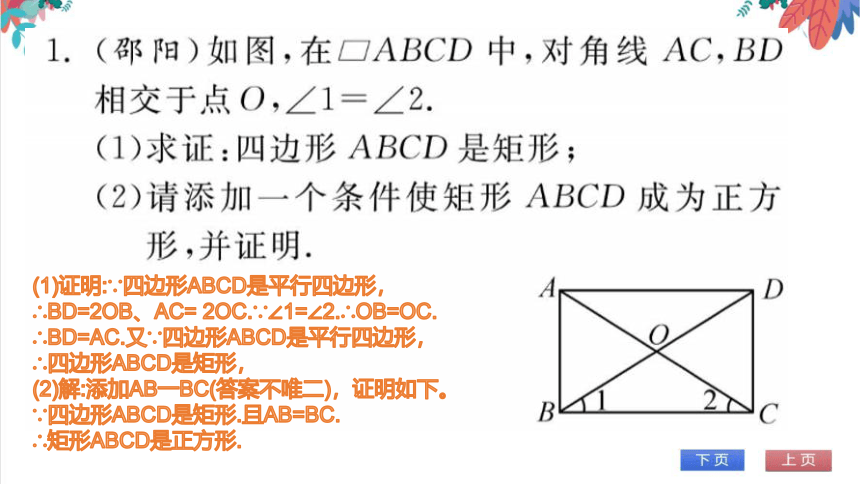
(1)证明:∵四边形ABCD是平行四边形,
∴BD=2OB、AC= 2OC.∵∠1=∠2.∴OB=OC.
∴BD=AC.又∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
(2)解:添加AB一BC(答案不唯二),证明如下。
∵四边形ABCD是矩形.且AB=BC.
∴矩形ABCD是正方形.
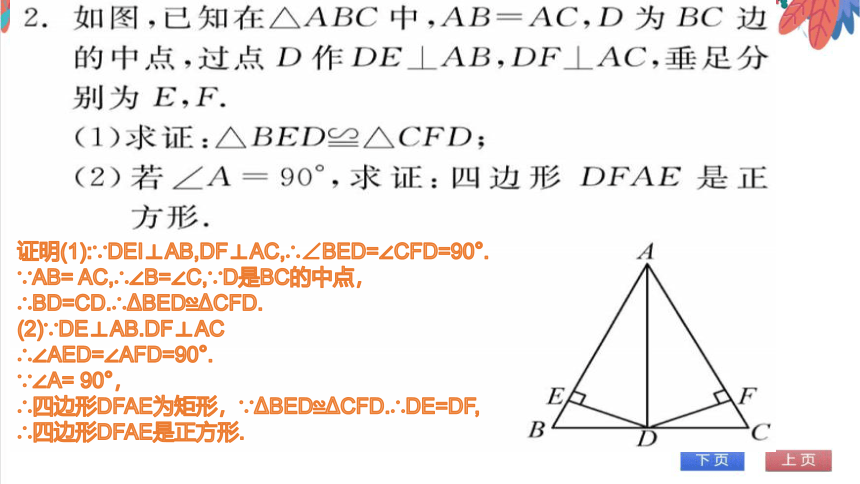
证明(1):∵DEI⊥AB,DF⊥AC,∴∠BED=∠CFD=90°.
∵AB= AC,∴∠B=∠C,∵D是BC的中点,
∴BD=CD.∴ BED≌ CFD.
(2)∵DE⊥AB.DF⊥AC
∴∠AED=∠AFD=90°.
∵∠A= 90°,
∴四边形DFAE为矩形,∵ BED≌ CFD.∴DE=DF,
∴四边形DFAE是正方形.
45°
(1)证明:∵O是CD的中点,∴OD=OC.
∵四边形ABCD是平行四边形,∴AD// BC.
∴∠ADO= ∠OCE.在 AOD和 EOC中,
∠ADO=∠OCE.OD=OC,∠AOD=∠EOC,
∴ AOD≌ EOC(ASA)
(2)当∠B=∠AEB= 45°时,四边形ACED为正方形,理由如下:∵ AOD≌ EOC,
∴OA=OE,OC= OD,∴四边形ACED是平行四边形.
∴.AD=CE .∵四边形ABCD是平行四边形,∴AD=BC.∴BC=CE.
∵∠B=∠AEB=45,∴∠BAE= 90°.ACED是菱形,∵∠B= AEB,∴AB=AE.又∵BC=CE,∴AC⊥BE,∴∠ACE=90°.又∵四边形ACED是菱形,∴四边形ACED是正方形
解:(1)四边形AEDF是菱形。
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.又∵EF垂直平分AD.∴∠AOE=∠AOF=90°
又∵AO=AO,∴ AOE≌ AOF.∴OE=OF
∵EF重直平分AD.∴OA=OD, ∴四边形AEDF是平行四边形。
∵EF⊥AD,∴四边形AEDF是菱形.
(2)当 ABC满足∠BAC=90°时,四边形AEDF是正方形
理由:在 ABC,当∠BAC=90°,∵四边形AEDF是菱形,
∴四边形AEDF是正方形。
≌
专题训练(四)
判定正方形两捷径
(1)证明:∵四边形ABCD是平行四边形,
∴BD=2OB、AC= 2OC.∵∠1=∠2.∴OB=OC.
∴BD=AC.又∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
(2)解:添加AB一BC(答案不唯二),证明如下。
∵四边形ABCD是矩形.且AB=BC.
∴矩形ABCD是正方形.
证明(1):∵DEI⊥AB,DF⊥AC,∴∠BED=∠CFD=90°.
∵AB= AC,∴∠B=∠C,∵D是BC的中点,
∴BD=CD.∴ BED≌ CFD.
(2)∵DE⊥AB.DF⊥AC
∴∠AED=∠AFD=90°.
∵∠A= 90°,
∴四边形DFAE为矩形,∵ BED≌ CFD.∴DE=DF,
∴四边形DFAE是正方形.
45°
(1)证明:∵O是CD的中点,∴OD=OC.
∵四边形ABCD是平行四边形,∴AD// BC.
∴∠ADO= ∠OCE.在 AOD和 EOC中,
∠ADO=∠OCE.OD=OC,∠AOD=∠EOC,
∴ AOD≌ EOC(ASA)
(2)当∠B=∠AEB= 45°时,四边形ACED为正方形,理由如下:∵ AOD≌ EOC,
∴OA=OE,OC= OD,∴四边形ACED是平行四边形.
∴.AD=CE .∵四边形ABCD是平行四边形,∴AD=BC.∴BC=CE.
∵∠B=∠AEB=45,∴∠BAE= 90°.ACED是菱形,∵∠B= AEB,∴AB=AE.又∵BC=CE,∴AC⊥BE,∴∠ACE=90°.又∵四边形ACED是菱形,∴四边形ACED是正方形
解:(1)四边形AEDF是菱形。
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.又∵EF垂直平分AD.∴∠AOE=∠AOF=90°
又∵AO=AO,∴ AOE≌ AOF.∴OE=OF
∵EF重直平分AD.∴OA=OD, ∴四边形AEDF是平行四边形。
∵EF⊥AD,∴四边形AEDF是菱形.
(2)当 ABC满足∠BAC=90°时,四边形AEDF是正方形
理由:在 ABC,当∠BAC=90°,∵四边形AEDF是菱形,
∴四边形AEDF是正方形。
≌
