2022年人教版七年级数学 下册 8.2 消元—解二元一次方程组(1)代入法 课件(共25张)
文档属性
| 名称 | 2022年人教版七年级数学 下册 8.2 消元—解二元一次方程组(1)代入法 课件(共25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 966.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 11:06:31 | ||
图片预览







文档简介
(共25张PPT)
问题:体育节要到了,篮球是七年级(1)班的拳头项目.为了取得好名次,他们想在全部22场比赛中得到40分.已知每场比赛都要分出胜负,胜队得2分,负队得1分.那么七年级(1)班应该胜、负各几场
你会用二元一次方程组解决这个问题吗
根据问题中的等量关系,设胜x场,负y场,可以更容易地列出方程:
x+y=22, ①
2x+y=40.②
那么有哪些方法可以求得二元一次方程组的解呢
8.2 消元—解二元一次方程组
第1课时 代入法
人教版七年级数学 下册
1.领会并总结解二元一次方程组的方法,根据方程组的情况,能恰当地应用“代入消元法”解方程组.
2.提高逻辑思维能力、计算能力、解决实际问题的能力.
学习目标
认真阅读课本中8.2 消元——解二元一次方程组的内容,完成下面练习并体验知识点的形成过程。
自主研学
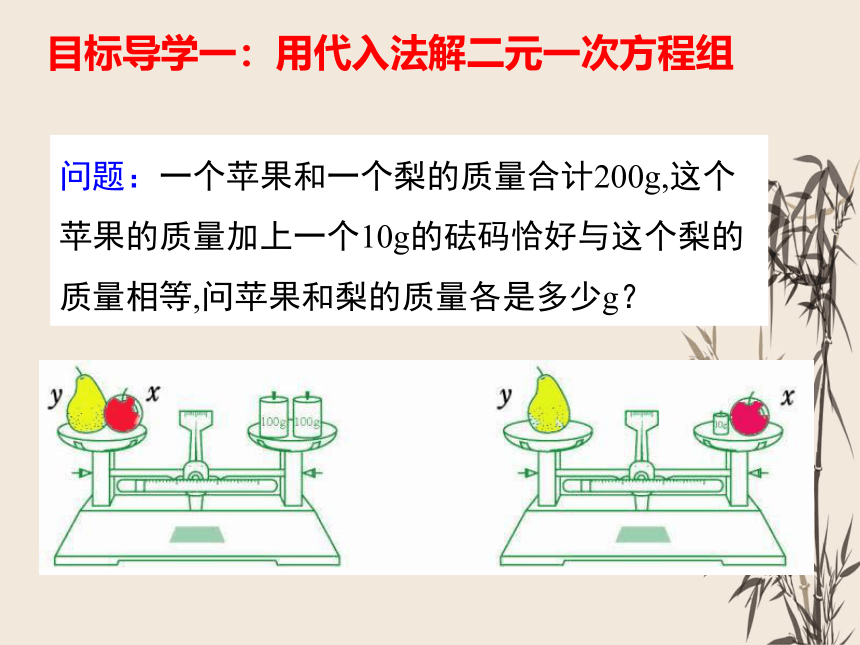
问题:一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
目标导学一:用代入法解二元一次方程组
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
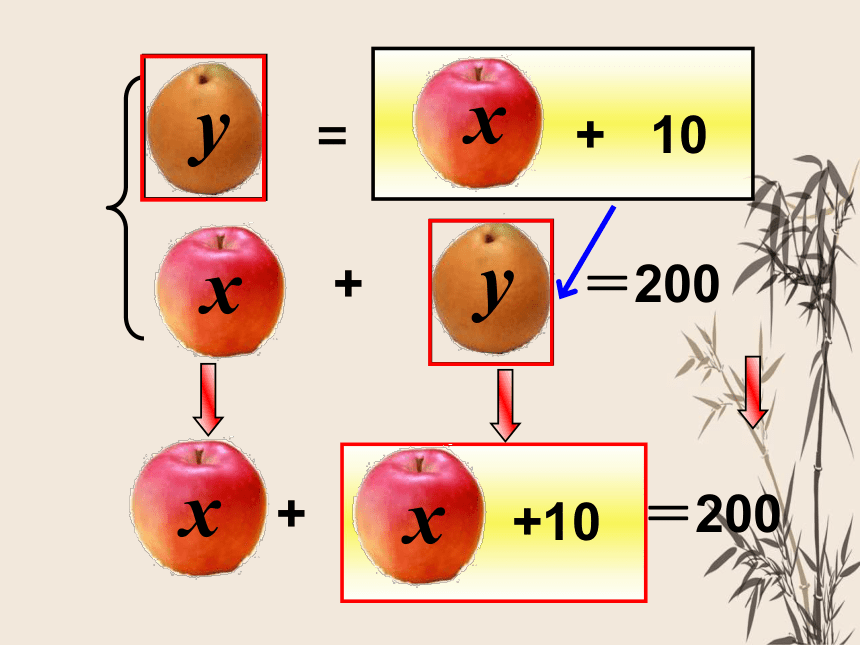
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法.
代入法是解二元一次方程组常用的方法之一.
知识归纳
例1 用代入法解方程组
解:把①代入②,得
3(y+3)-8y=14,
所以y=-1.
把y=-1代入①,得x=2.
1、变形:将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值
3、回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值
4、写解
典型例题
1.把下列方程改写成用含x的式子表示y的形式.
(1)2x-y=3; (2)3x+y-1=0.
2.用代入法解下列方程组:
1.(1)y=2x-3;(2)y=1-3x.
答案:
即学即练
观察上面的方程和方程组,你能发现二者之间的联系吗?请你尝试求得方程组的解。(先试着独立完成,然后与你的同伴交流做法)
1.为什么能替换?
代表了同一个量
二元一次方程组 一元一次方程
消元
2.代入前后的方程组发生了怎样的变化 (代入的作用)
化归思想
代入
例2:解方程组:
解:
由①得,y=3x-5,③
把③带入②,得5x-2(3x-5)=0.8
解得x=9.2。
把x=9.2代入③得,y=22.6。
所以原方程组的解是
典型例题
解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的一个方程中,可得一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
步骤归纳
用代入消元法解二元一次方程组时,尽量选取未知数系数的绝对值是1的方程进行变形;若未知数系数的绝对值都不是1,则选取系数的绝对值较小的方程变形.
温馨提示
例3.篮球联赛中,每场比赛都要分出胜负,胜一场得2分.负一场得1分,某队为了争取较好名次,想在全部20场比赛中得到35分,那么这个队胜负场数分别是多少?
解 设胜的场数是x,负的场数是y,可列方程组:
由①得 y=20-x . ③
将③代入②,得 2x+20-x=35 .
解得 x=15.
将 x=15代入③得y=5.则这个方程组的解是
答:这个队胜15场,负5场.
①
②
目标导学二:代入法解二元一次方程组的简单应用
张翔从学校出发骑自行车去县城,中途因道路施工
步行一段路,1.5 h后到达县城.他骑车的平均速度是
15 km/h,步行的平均速度是5 km/h,路程全长20 km.
他骑车与步行各用多少时间
解:设他骑车用的时间为x h ,则他步行用的时间为(1.5-x) h.根据题意,得15x+5(1.5-x)=20.
解得x=1.25. 则1.5-1.25=0.25( h ).
答:他骑车用了1.25 h ,步行用了0.25 h .
即学即练
1.二元一次方程组
代入消元法
一元一次方程
2.代入消元法的一般步骤:
3.思想方法:转化思想、消元思想、方程(组)思想.
变
代
求
写
转化
课堂小结
1. 已知 是二元一次方程组 的解,则a-b的值为( )。
B
A.
B.
C.
D.
1
-1
2
3
检测目标
2. 解方程组:
由①,得x+1=6y。
解:
把x+1=6y代入②,得2×6y-y=11,解得y=1。
把y=1代入①,得 =2×1,x=5。
所以原方程组的解为
检测目标
3. 用代入法解下列方程组:
3y=-7,y= 。
把y= 代入⑤,得x=-3。
所以原方程组的解是
解:
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
问题:体育节要到了,篮球是七年级(1)班的拳头项目.为了取得好名次,他们想在全部22场比赛中得到40分.已知每场比赛都要分出胜负,胜队得2分,负队得1分.那么七年级(1)班应该胜、负各几场
你会用二元一次方程组解决这个问题吗
根据问题中的等量关系,设胜x场,负y场,可以更容易地列出方程:
x+y=22, ①
2x+y=40.②
那么有哪些方法可以求得二元一次方程组的解呢
8.2 消元—解二元一次方程组
第1课时 代入法
人教版七年级数学 下册
1.领会并总结解二元一次方程组的方法,根据方程组的情况,能恰当地应用“代入消元法”解方程组.
2.提高逻辑思维能力、计算能力、解决实际问题的能力.
学习目标
认真阅读课本中8.2 消元——解二元一次方程组的内容,完成下面练习并体验知识点的形成过程。
自主研学
问题:一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
目标导学一:用代入法解二元一次方程组
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法.
代入法是解二元一次方程组常用的方法之一.
知识归纳
例1 用代入法解方程组
解:把①代入②,得
3(y+3)-8y=14,
所以y=-1.
把y=-1代入①,得x=2.
1、变形:将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值
3、回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值
4、写解
典型例题
1.把下列方程改写成用含x的式子表示y的形式.
(1)2x-y=3; (2)3x+y-1=0.
2.用代入法解下列方程组:
1.(1)y=2x-3;(2)y=1-3x.
答案:
即学即练
观察上面的方程和方程组,你能发现二者之间的联系吗?请你尝试求得方程组的解。(先试着独立完成,然后与你的同伴交流做法)
1.为什么能替换?
代表了同一个量
二元一次方程组 一元一次方程
消元
2.代入前后的方程组发生了怎样的变化 (代入的作用)
化归思想
代入
例2:解方程组:
解:
由①得,y=3x-5,③
把③带入②,得5x-2(3x-5)=0.8
解得x=9.2。
把x=9.2代入③得,y=22.6。
所以原方程组的解是
典型例题
解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的一个方程中,可得一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
步骤归纳
用代入消元法解二元一次方程组时,尽量选取未知数系数的绝对值是1的方程进行变形;若未知数系数的绝对值都不是1,则选取系数的绝对值较小的方程变形.
温馨提示
例3.篮球联赛中,每场比赛都要分出胜负,胜一场得2分.负一场得1分,某队为了争取较好名次,想在全部20场比赛中得到35分,那么这个队胜负场数分别是多少?
解 设胜的场数是x,负的场数是y,可列方程组:
由①得 y=20-x . ③
将③代入②,得 2x+20-x=35 .
解得 x=15.
将 x=15代入③得y=5.则这个方程组的解是
答:这个队胜15场,负5场.
①
②
目标导学二:代入法解二元一次方程组的简单应用
张翔从学校出发骑自行车去县城,中途因道路施工
步行一段路,1.5 h后到达县城.他骑车的平均速度是
15 km/h,步行的平均速度是5 km/h,路程全长20 km.
他骑车与步行各用多少时间
解:设他骑车用的时间为x h ,则他步行用的时间为(1.5-x) h.根据题意,得15x+5(1.5-x)=20.
解得x=1.25. 则1.5-1.25=0.25( h ).
答:他骑车用了1.25 h ,步行用了0.25 h .
即学即练
1.二元一次方程组
代入消元法
一元一次方程
2.代入消元法的一般步骤:
3.思想方法:转化思想、消元思想、方程(组)思想.
变
代
求
写
转化
课堂小结
1. 已知 是二元一次方程组 的解,则a-b的值为( )。
B
A.
B.
C.
D.
1
-1
2
3
检测目标
2. 解方程组:
由①,得x+1=6y。
解:
把x+1=6y代入②,得2×6y-y=11,解得y=1。
把y=1代入①,得 =2×1,x=5。
所以原方程组的解为
检测目标
3. 用代入法解下列方程组:
3y=-7,y= 。
把y= 代入⑤,得x=-3。
所以原方程组的解是
解:
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
