2022年人教版七年级数学 下册 8.3 实际问题与二元一次方程组 课件(共31张)
文档属性
| 名称 | 2022年人教版七年级数学 下册 8.3 实际问题与二元一次方程组 课件(共31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
1.二元一次方程组
代入消元法
一元一次方程
2.代入消元法的一般步骤:
3.思想方法:转化思想、消元思想、方程(组)思想.
变
代
求
写
转化
知识回顾
我们学过哪几种解二元一次方程组的方法?
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄
新课导入
8.3 实际问题与二元一次方程组
人教版七年级数学 下册
目标导航
1.能够根据具体的数量关系,列出二元一次方程组解决实际问题.(重点)
2.学会利用二元一次方程组解决几何、行程问题.(重点、难点)
3.经历和体验方程组解决实际问题的过程.
目标导航一
用二元一次方程组解决
简单的实际问题
1.简单实际问题
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李
大叔估计的准确吗?
目标导学一:列方程组解决简单实际问题
合作与交流
问题1 题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;
每头小牛1天需用的饲料.
问题2 题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用
饲料为xkg和ykg,
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组:x= ,
y= .
20
5
解题小结:用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解
出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,
然后作答.
总结归纳
数量关系
字母
2
代入消元
加减消元法
第一个数与第二个数的和是67,第一个数与第二个数的差是21.求这两个数.
解此方程组,得
x+ y=67
x- y=21
x=44
y=23
答:第一个数为44,第二个数为23.
解:设第一个数为x,第二个数为y,
由题意得
即学即练
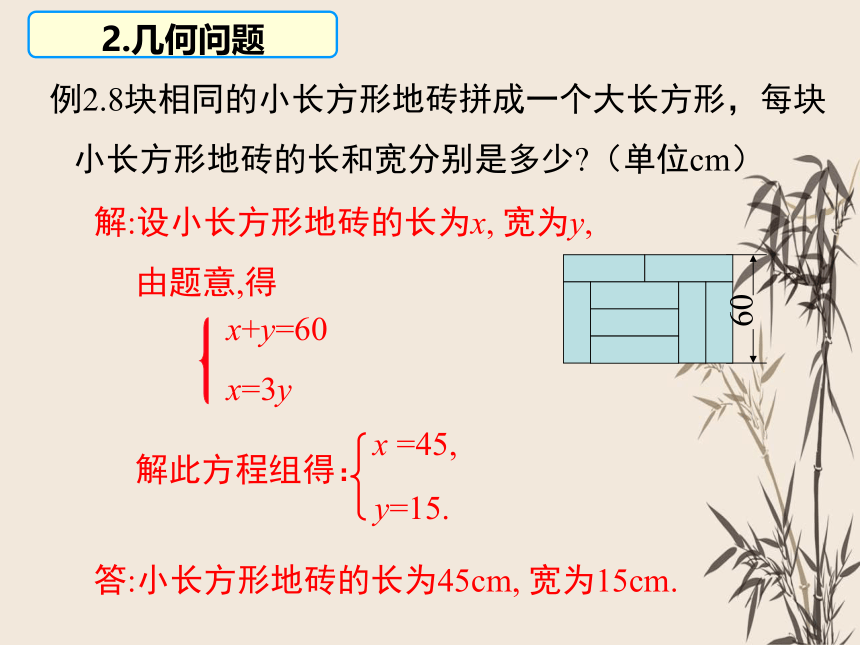
例2.8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (单位cm)
60
x+y=60
x=3y
解:设小长方形地砖的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
2.几何问题
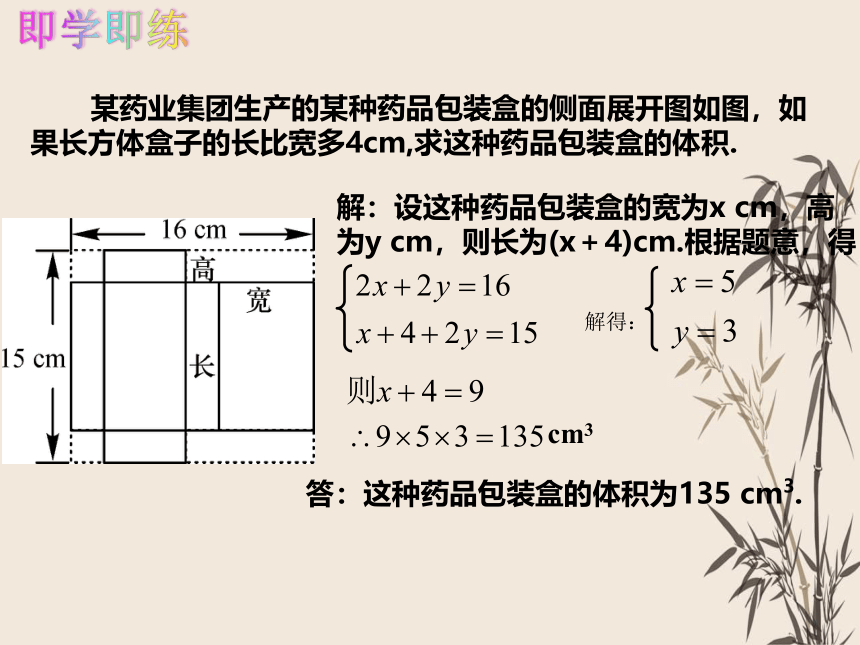
某药业集团生产的某种药品包装盒的侧面展开图如图,如果长方体盒子的长比宽多4cm,求这种药品包装盒的体积.
解:设这种药品包装盒的宽为x cm,高为y cm,则长为(x+4)cm.根据题意,得
解得:
cm3
答:这种药品包装盒的体积为135 cm3.
即学即练
例3 甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
3.行程问题
(1) 同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
答:甲的速度为5km/h,乙的速度为3km/h.
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄
解决问题
顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
解决问题
解:设悟空行走速度是每分钟x里,风速是每 分钟y里。
依题意,得
4(x-y)=600
x=200 y=50
答:风速是每分钟50里.
4(x+y)=1000
解得
甲、乙两人都从A地到B地,甲步行,乙骑自行车,如果甲先走6千米乙再动身,则乙走 小时后恰好与甲同时到达B地;如果甲先走1小时,那么乙用 小时可追上甲,求两人的速度.
解:设甲的速度为x千米/时,乙的速度为y千米/时,则
答:甲的速度为4千米/时,乙的速度为12千米/时.
即学即练
例4 如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
·
长青化工厂
公路10千米
目标导学二:列方程组解决较复杂的实际问题
分析:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
价 值(元)
铁路运费(元)
公路运费(元)
合 计
原料y吨
产品x吨
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8 000x-1 000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元.
1.5 × 20x+ 1.5×10y=15 000,
1.2 × 110x+ 1.2×120y=97 200.
解此方程组,得
x=19
y=1
即
x+y=20
4x+5y=81
答:甲种盐水的浓度为19%,乙种盐水的浓度为1% 。
解:设甲种盐水的浓度为x%,乙种盐水的浓度为y% 。
1 种情况
2 种情况
混合前
混合后
100 x%
400 x%
100 y%
500y%,
200× 10%
900×9%
甲.乙两种盐水各取100克混合,所得盐水含盐为10%,
若甲种盐水取400克,乙种盐水取500克混合,所得盐水含盐
为9%,问甲.乙两种盐水的浓度分别是多少?
甲种盐水
含盐重量
乙种盐水
含盐重量
乙种盐水
含盐重量
甲种盐水
含盐重量
依题意,得
100 x% +100 y% = 200× 10%
400 x% + 500y%=900×9%
即学即练
关于浓度问题的概念:
溶液=溶质+溶剂
溶质=浓度×溶液
混合前溶液的和=混合后的溶液
混合前溶质的和=混合后的溶质
列方程组解应用题也要检验,既要代入方程组中,还要代入题目中检验。
依据是:
等量关系是:
知识补充
应用二元一次方程组解决实际问题的基本步骤:
分析问题
抽象问题
转化问题
解决问题
实际
问题
分析
抽象
方程(组)
求解
检验
问题
解决
课堂小结
1.欲将某河上游A地的一部分牧场改为林场.改变后,林场和牧场共有160公顷, 林场面积是牧场面积的7倍, 试问完成后林场、牧场的面积各为多少公顷?
解:设完成后林场面积为x公顷,牧场面积为y公顷。根据题意,有
解这个方程组,得
答:完成后林场面积为140公顷,牧场面积为20公顷.
x+y=160
x=7y
x=140
y=20
检测目标
2.我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9个小时就能到达南京;返回时则用多了1个小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
检测目标
3.某工地挖掘机的台数和装卸机的台数之和为21,如果每台挖掘机每天平均挖土750m3,每台装卸机每天平均运土300m3,正好能使挖出的土及时运走,问挖掘机有多少台?装卸机有多少台?
解:设挖掘机x台,装卸机y台,根据题意列出方程组得
解得
答:挖掘机有6台,装卸机有15台.
检测目标
4.某人用24000元买进甲、乙两种股票,在甲股票升值15%,
乙股票下跌10%时卖出,共获利1350元,试问某人买的甲、乙两股票各是多少元?
解:设甲种股票买x元,乙种股票买y元。
依题意,得
x+y=24000
15% x - 10% y=1350
即
3x - 2y=27000
x+y=24000
解此方程组,得
x=15000
y=9000
答:甲种股票买15000元,乙种股票买9000元。
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
1.二元一次方程组
代入消元法
一元一次方程
2.代入消元法的一般步骤:
3.思想方法:转化思想、消元思想、方程(组)思想.
变
代
求
写
转化
知识回顾
我们学过哪几种解二元一次方程组的方法?
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄
新课导入
8.3 实际问题与二元一次方程组
人教版七年级数学 下册
目标导航
1.能够根据具体的数量关系,列出二元一次方程组解决实际问题.(重点)
2.学会利用二元一次方程组解决几何、行程问题.(重点、难点)
3.经历和体验方程组解决实际问题的过程.
目标导航一
用二元一次方程组解决
简单的实际问题
1.简单实际问题
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李
大叔估计的准确吗?
目标导学一:列方程组解决简单实际问题
合作与交流
问题1 题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;
每头小牛1天需用的饲料.
问题2 题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用
饲料为xkg和ykg,
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组:x= ,
y= .
20
5
解题小结:用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解
出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,
然后作答.
总结归纳
数量关系
字母
2
代入消元
加减消元法
第一个数与第二个数的和是67,第一个数与第二个数的差是21.求这两个数.
解此方程组,得
x+ y=67
x- y=21
x=44
y=23
答:第一个数为44,第二个数为23.
解:设第一个数为x,第二个数为y,
由题意得
即学即练
例2.8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (单位cm)
60
x+y=60
x=3y
解:设小长方形地砖的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
2.几何问题
某药业集团生产的某种药品包装盒的侧面展开图如图,如果长方体盒子的长比宽多4cm,求这种药品包装盒的体积.
解:设这种药品包装盒的宽为x cm,高为y cm,则长为(x+4)cm.根据题意,得
解得:
cm3
答:这种药品包装盒的体积为135 cm3.
即学即练
例3 甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
3.行程问题
(1) 同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
答:甲的速度为5km/h,乙的速度为3km/h.
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄
解决问题
顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
解决问题
解:设悟空行走速度是每分钟x里,风速是每 分钟y里。
依题意,得
4(x-y)=600
x=200 y=50
答:风速是每分钟50里.
4(x+y)=1000
解得
甲、乙两人都从A地到B地,甲步行,乙骑自行车,如果甲先走6千米乙再动身,则乙走 小时后恰好与甲同时到达B地;如果甲先走1小时,那么乙用 小时可追上甲,求两人的速度.
解:设甲的速度为x千米/时,乙的速度为y千米/时,则
答:甲的速度为4千米/时,乙的速度为12千米/时.
即学即练
例4 如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
·
长青化工厂
公路10千米
目标导学二:列方程组解决较复杂的实际问题
分析:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
价 值(元)
铁路运费(元)
公路运费(元)
合 计
原料y吨
产品x吨
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8 000x-1 000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元.
1.5 × 20x+ 1.5×10y=15 000,
1.2 × 110x+ 1.2×120y=97 200.
解此方程组,得
x=19
y=1
即
x+y=20
4x+5y=81
答:甲种盐水的浓度为19%,乙种盐水的浓度为1% 。
解:设甲种盐水的浓度为x%,乙种盐水的浓度为y% 。
1 种情况
2 种情况
混合前
混合后
100 x%
400 x%
100 y%
500y%,
200× 10%
900×9%
甲.乙两种盐水各取100克混合,所得盐水含盐为10%,
若甲种盐水取400克,乙种盐水取500克混合,所得盐水含盐
为9%,问甲.乙两种盐水的浓度分别是多少?
甲种盐水
含盐重量
乙种盐水
含盐重量
乙种盐水
含盐重量
甲种盐水
含盐重量
依题意,得
100 x% +100 y% = 200× 10%
400 x% + 500y%=900×9%
即学即练
关于浓度问题的概念:
溶液=溶质+溶剂
溶质=浓度×溶液
混合前溶液的和=混合后的溶液
混合前溶质的和=混合后的溶质
列方程组解应用题也要检验,既要代入方程组中,还要代入题目中检验。
依据是:
等量关系是:
知识补充
应用二元一次方程组解决实际问题的基本步骤:
分析问题
抽象问题
转化问题
解决问题
实际
问题
分析
抽象
方程(组)
求解
检验
问题
解决
课堂小结
1.欲将某河上游A地的一部分牧场改为林场.改变后,林场和牧场共有160公顷, 林场面积是牧场面积的7倍, 试问完成后林场、牧场的面积各为多少公顷?
解:设完成后林场面积为x公顷,牧场面积为y公顷。根据题意,有
解这个方程组,得
答:完成后林场面积为140公顷,牧场面积为20公顷.
x+y=160
x=7y
x=140
y=20
检测目标
2.我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9个小时就能到达南京;返回时则用多了1个小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
检测目标
3.某工地挖掘机的台数和装卸机的台数之和为21,如果每台挖掘机每天平均挖土750m3,每台装卸机每天平均运土300m3,正好能使挖出的土及时运走,问挖掘机有多少台?装卸机有多少台?
解:设挖掘机x台,装卸机y台,根据题意列出方程组得
解得
答:挖掘机有6台,装卸机有15台.
检测目标
4.某人用24000元买进甲、乙两种股票,在甲股票升值15%,
乙股票下跌10%时卖出,共获利1350元,试问某人买的甲、乙两股票各是多少元?
解:设甲种股票买x元,乙种股票买y元。
依题意,得
x+y=24000
15% x - 10% y=1350
即
3x - 2y=27000
x+y=24000
解此方程组,得
x=15000
y=9000
答:甲种股票买15000元,乙种股票买9000元。
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
