29.3课题学习制作立体模型(课件)-(共28张PPT)
文档属性
| 名称 | 29.3课题学习制作立体模型(课件)-(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 11:10:23 | ||
图片预览





文档简介
(共28张PPT)
29.3 课题学习 制作立体模型
第二十九章 投影与视图
2021-2022学年九年级数学下册(人教版)
(1)体验平面图形向立体图形转化的过程.
(2)体会用三视图表示立体图形的作用.
(3)进一步感受平面图形与立体图形之间
的关系.
学习目标
观察三视图,并综合考虑各视图表达的含义以及视图间的联系,可以想象出三视图所表示的立体图形的形状,这是由视图转化为立体图形的过程.
怎样由视图转化为立体图形?
这节课我们通过动手实践,来体会这个过程.
情景导入
一、工具准备
刻度尺、剪刀、小刀、胶水、硬纸板、马铃薯(或萝卜).
探究新知
二、具体活动
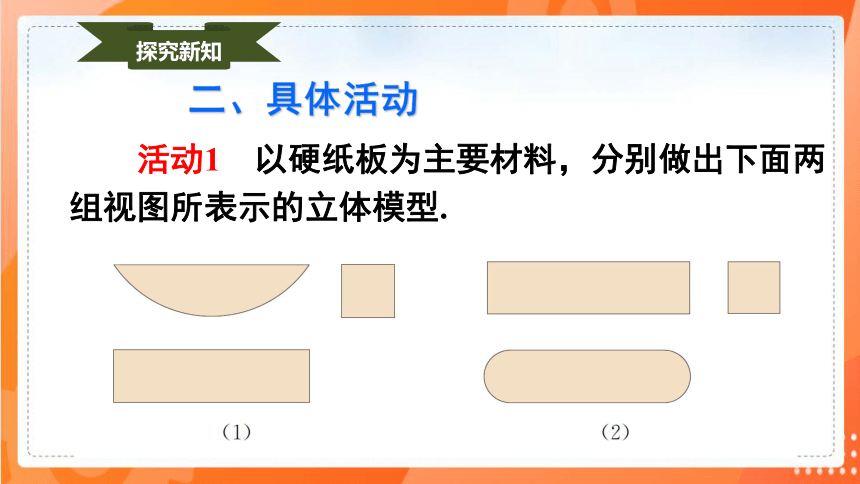
活动1 以硬纸板为主要材料,分别做出下面两组视图所表示的立体模型.
探究新知
活动2 按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型.
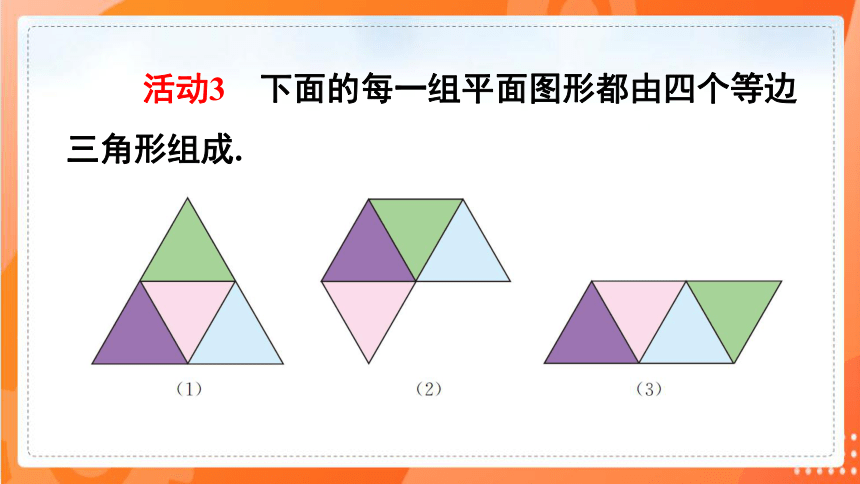
活动3 下面的每一组平面图形都由四个等边三角形组成.
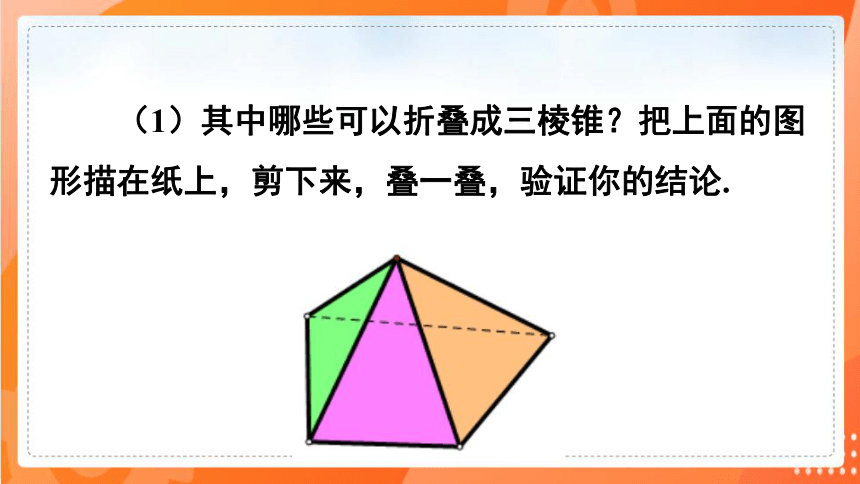
(1)其中哪些可以折叠成三棱锥?把上面的图形描在纸上,剪下来,叠一叠,验证你的结论.
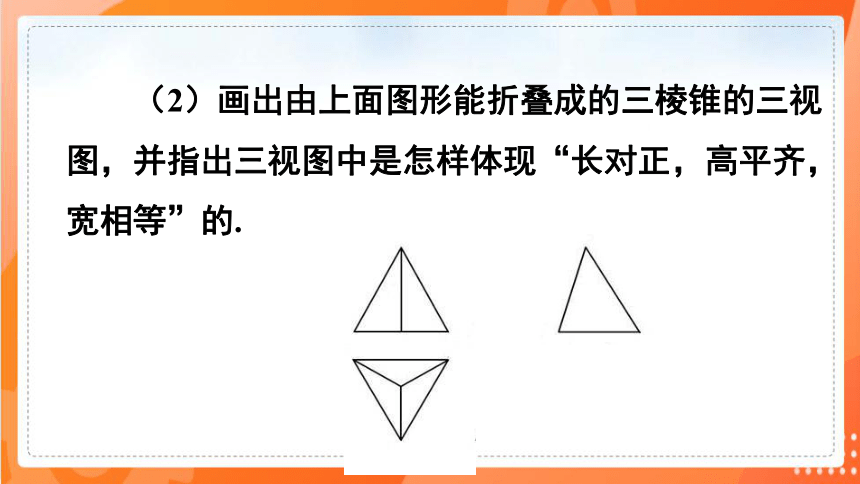
(2)画出由上面图形能折叠成的三棱锥的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的.
(3)如果上图中小三角形的边长为1,那么对应的三棱锥的表面积是多少?
活动4 下面的图形由一个扇形和一个圆的组成.
(1)把上面的图形描在纸上,剪下来,围成一个圆锥.
(2)画出由上面图形围成的圆锥的三视图.
(3)如果上图中扇形的半径为13,圆的半径为5,那么对应的圆锥的体积是多少?
13
12
5
V= r h
= 5 12
=
1.某几何体的三视图如图所示,则这个几何体是( )
A
巩固提高
2.下列平面展开图是由5个大小相同的正方形组成的,其中沿正方形的边不能折成无盖小方盒的是( )
A B C D
B
3.如图是某几何体的平面展开图,求图中小圆的半径.
解
1.如图是一个上下底密封的纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积.(结果可保留根号)
解:
合作探究
2.如图,长方体长为4 cm,宽为2 cm,高为5 cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,求蚂蚁爬行的最短路径长.
合作探究
解 作出这个长方体的侧面展开图,则最短路径如图为PQ.
展开
圆柱
应用拓展
展开
圆锥
应用拓展
一 四 一型
二 三 一型
阶 梯 型
正方体的展开图
应用拓展
1.下列图形是正方体的展开图吗
不是
不是
不是
是
是
是
强化提升
2.在正方体的展开图中,找出与“我”相对的面.
(1)
(6)
(5)
(4)
(3)
(2)
我
为
一
八
以
我
师
奋
勤
力
努
要
我
要
我
长
傲
骄
我
以
一
八
荣
我
创
要
于
们
新
并
勇
肩
奋
斗
敬
尊
强化提升
3、下图是右边正方体的展开图的是( )
A
D
C
B
B
强化提升
4、如图是正方体的展开图,
请根据各面上的图案判断这
个正方体是( )
A
D
C
B
C
强化提升
https://www.21cnjy.com/help/help_extract.php
29.3 课题学习 制作立体模型
第二十九章 投影与视图
2021-2022学年九年级数学下册(人教版)
(1)体验平面图形向立体图形转化的过程.
(2)体会用三视图表示立体图形的作用.
(3)进一步感受平面图形与立体图形之间
的关系.
学习目标
观察三视图,并综合考虑各视图表达的含义以及视图间的联系,可以想象出三视图所表示的立体图形的形状,这是由视图转化为立体图形的过程.
怎样由视图转化为立体图形?
这节课我们通过动手实践,来体会这个过程.
情景导入
一、工具准备
刻度尺、剪刀、小刀、胶水、硬纸板、马铃薯(或萝卜).
探究新知
二、具体活动
活动1 以硬纸板为主要材料,分别做出下面两组视图所表示的立体模型.
探究新知
活动2 按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型.
活动3 下面的每一组平面图形都由四个等边三角形组成.
(1)其中哪些可以折叠成三棱锥?把上面的图形描在纸上,剪下来,叠一叠,验证你的结论.
(2)画出由上面图形能折叠成的三棱锥的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的.
(3)如果上图中小三角形的边长为1,那么对应的三棱锥的表面积是多少?
活动4 下面的图形由一个扇形和一个圆的组成.
(1)把上面的图形描在纸上,剪下来,围成一个圆锥.
(2)画出由上面图形围成的圆锥的三视图.
(3)如果上图中扇形的半径为13,圆的半径为5,那么对应的圆锥的体积是多少?
13
12
5
V= r h
= 5 12
=
1.某几何体的三视图如图所示,则这个几何体是( )
A
巩固提高
2.下列平面展开图是由5个大小相同的正方形组成的,其中沿正方形的边不能折成无盖小方盒的是( )
A B C D
B
3.如图是某几何体的平面展开图,求图中小圆的半径.
解
1.如图是一个上下底密封的纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积.(结果可保留根号)
解:
合作探究
2.如图,长方体长为4 cm,宽为2 cm,高为5 cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,求蚂蚁爬行的最短路径长.
合作探究
解 作出这个长方体的侧面展开图,则最短路径如图为PQ.
展开
圆柱
应用拓展
展开
圆锥
应用拓展
一 四 一型
二 三 一型
阶 梯 型
正方体的展开图
应用拓展
1.下列图形是正方体的展开图吗
不是
不是
不是
是
是
是
强化提升
2.在正方体的展开图中,找出与“我”相对的面.
(1)
(6)
(5)
(4)
(3)
(2)
我
为
一
八
以
我
师
奋
勤
力
努
要
我
要
我
长
傲
骄
我
以
一
八
荣
我
创
要
于
们
新
并
勇
肩
奋
斗
敬
尊
强化提升
3、下图是右边正方体的展开图的是( )
A
D
C
B
B
强化提升
4、如图是正方体的展开图,
请根据各面上的图案判断这
个正方体是( )
A
D
C
B
C
强化提升
https://www.21cnjy.com/help/help_extract.php
