2021-2022学年人教版八年级数学下册《19.1.2函数的图像》课件(28张)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册《19.1.2函数的图像》课件(28张) |  | |
| 格式 | pptx | ||
| 文件大小 | 22.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 10:54:20 | ||
图片预览





文档简介
(共28张PPT)
19.1.2函数的图像
人教版八年级下册
第19章一次函数
01
了解函数图象的意义。
02
会根据函数图象分析函数的变化规律并解决具体问题。
教学目标
复习回顾
函数:
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
函数解析式:
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法,这种式子叫做函
数的解析式.
函数值:
对于自变量 x 在取值范围内的某个确定的值 a,函数 y 所对应的值为 b,即当 x=a 时,y=b,则 b 叫做当自变量的值为 a 时的函数值.
情景导入
生活中有很多函数关系难以列式子表示,通常用图像来直观地反映,例如用心电图表示心脏部位的生物电流与时间的关系。
这种表示函数的方法称为图象法
新知探究
即使对于能列式表示的函数关系,如果也能画图表示,那么会使函数关系更直观,例如正方形的面积。
如:正方形的边长为x,面积为S.
那么面积 S 随边长 x 变化的对应关系可表示为: S = x2 (x>0)
我们可以利用在坐标系中画函数图像的方法来表示S与x的关系吗?
新知探究
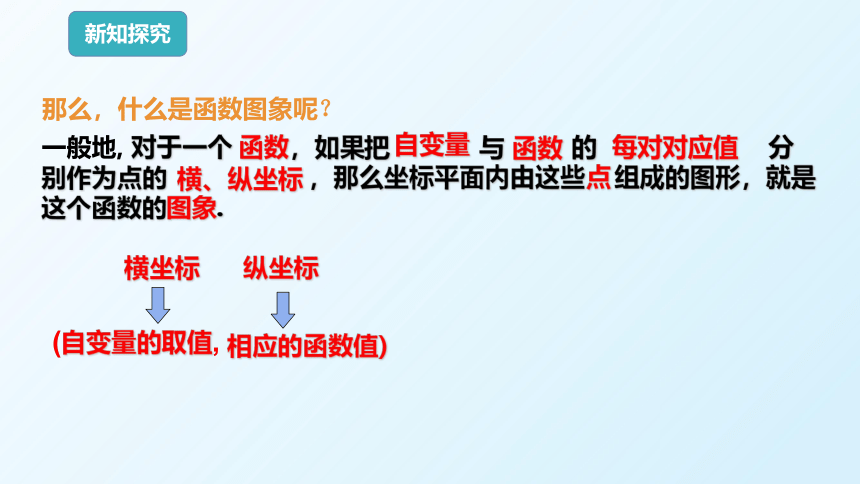
那么,什么是函数图象呢?
一般地, 对于一个 函数,如果把 与 的 分别作为点的 ,那么坐标平面内由这些 组成的图形,就是这个函数的图象.
自变量
函数
每对对应值
横、纵坐标
点
(自变量的取值,
相应的函数值)
纵坐标
横坐标
新知探究
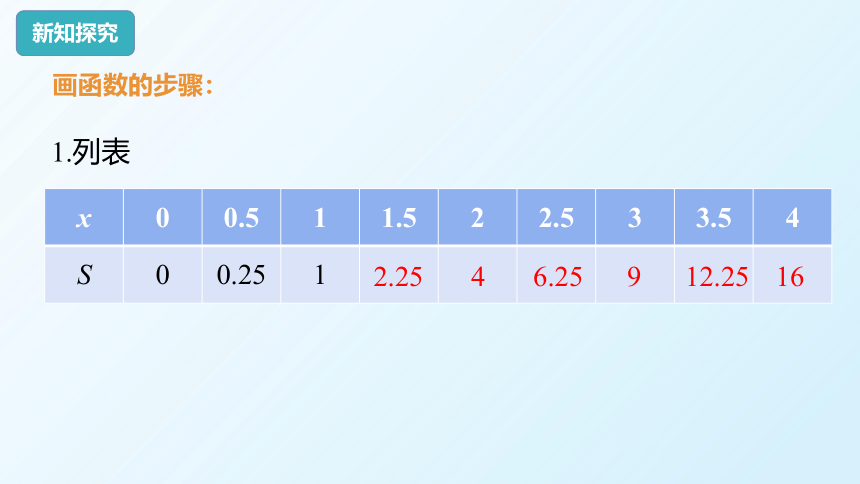
画函数的步骤:
1.列表
x 0 0.5 1 1.5 2 2.5 3 3.5 4
S 0 0.25 1
2.25
4
6.25
9
12.25
16
新知探究
O
1
2
3
4
1
4
9
16
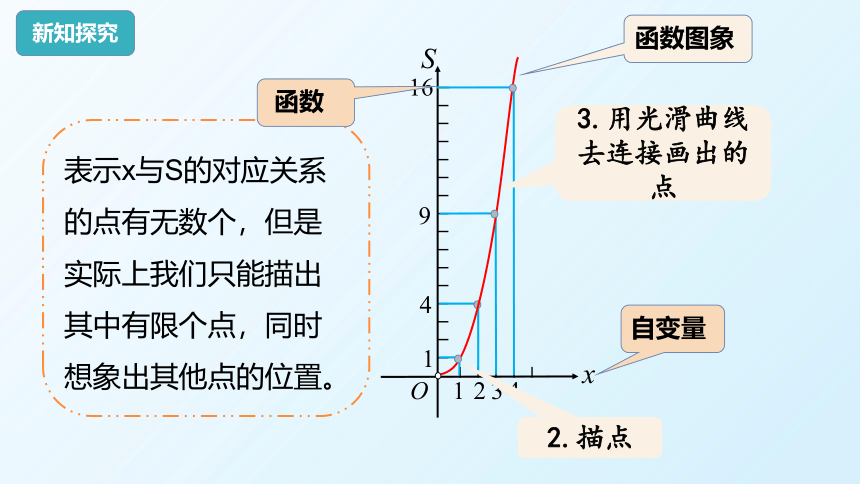
3.用光滑曲线去连接画出的点
表示x与S的对应关系的点有无数个,但是实际上我们只能描出其中有限个点,同时想象出其他点的位置。
x
S
2.描点
自变量
函数
函数图象
新知探究
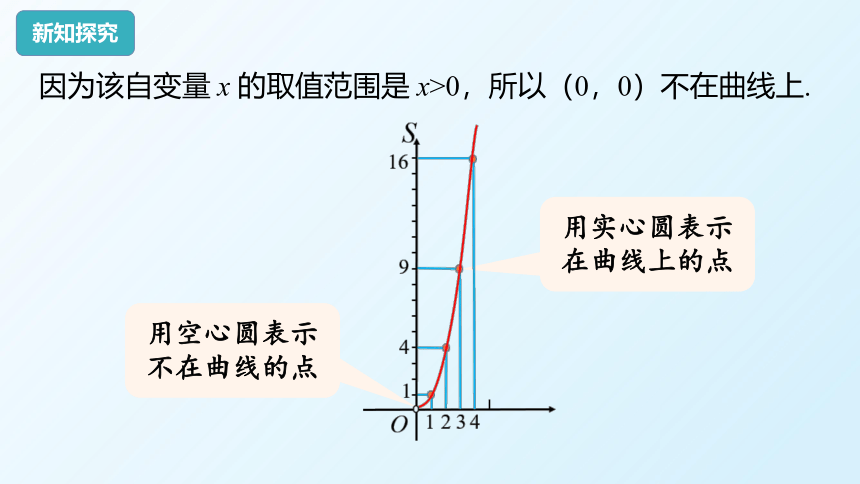
因为该自变量 x 的取值范围是 x>0,所以(0,0)不在曲线上.
用空心圆表示不在曲线的点
用实心圆表示在曲线上的点
归纳总结
1.函数图象:
一般地, 对于一个 函数,如果把 与 的 分别作为点的 ,那么坐标平面内由这些 组成的图形,就是这个函数的图象.
自变量
函数
每对对应值
横、纵坐标
点
函数的图象可以是直线、射线、线段,也可以是曲线,甚至可以是一些不连续的点.
归纳总结
2.函数图象的画法步骤
1
列表:表中给出一些自变量的值及其对应的函数值.
2
描点:在直角坐标系中,以自变量的值为横坐标,相对应的函数值为纵坐标,描出表格中数值对应的各点.
3
连线:按照横坐标由小到大的顺序,把所描出的各点用平滑的曲线连接起来.
新知探究
思考:下图是自动测温仪记录的图象,它反映了北京的春季某天气温 T 如何随时间 t 的变化而变化.你从图象中得到了哪些信息?
可以认为,气温T是时间t的函数,上图就是这个函数图象.
4
14
24
8
0
-3
T/℃
t/时
新知探究
(1)这一天中 时气温最低,最低气温为 度, 时气温最高,最高气温为___度.
横轴表示自变量t(时间)
纵轴表示对应的函数T(温度)
最高点
最低点
4
-3
14
8
4
14
24
8
0
-3
T/℃
t/时
(2)从 时至 时气温呈下降状态(即温度随时间的增长而下降), 从 时到 时气温呈上升状态,从 时至 时气温又呈下降状态。
0
4
4
14
14
24
(3)我们可以从图像中看出这一天中任一时刻的气温大约是多少。
归纳总结
1.解答图象信息题主要运用数形结合思想,化图象信息为数字信息.
主要步骤如下:
1
了解横、纵轴的意义;
2
从 上判定函数与自变量的关系;
图象形状
3
抓住图象中端点,拐点等特殊点的实际意义.
新知应用
根据图象回答下列问题:
8
25
28
58
68
x/min
0.8
0.6
y/km
O
例2 小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.下图反映了这个过程中,小明离家的距离y与时间x 之间的对应关系.
新知应用
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
解:由纵坐标看出,食堂离小明家0.6km;由横坐标看出,小明从家到食堂用了8min.
小明离开家的时间
小明与家的距离
小明从家里出发
小明到达食堂
新知应用
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(2)小明吃早餐用了多少时间?
由横坐标看出,25-8=17,小明吃早餐用了 17min.
小明到达食堂
距离不变,说明小明停留在某个地方
小明离开食堂
新知探究
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
由纵坐标看出,0.8-0.6=0.2,食堂离图书馆0.2km;由横坐标看出,
28-25=3,小明从食堂到图书馆用了3min.
小明到达图书馆
小明离开食堂
新知探究
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(4)小明读报用了多少时间?
由横坐标看出,58-28=30,小明读报用了30min.
小明到达图书馆
小明离开图书馆
距离不变,说明小明停留在某个地方
新知应用
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
由纵坐标看出,图书馆离小明家0.8km;由横坐标看出, 68-58=10,小明从图书馆回家用了10min,由此算出平均速度是0.08km/min.
小明离开图书馆
小明回到家了
课堂总结
函数的图像
定义:如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
画法:一列表;二描点;三连线.
数形结合:了解横、纵轴的意义,从图像形状上判断函数与自变量的关系,抓住图像中端点,拐点等特殊点的实际意义。
课堂练习
1.下列各曲线中不能表示y是x的函数是( ).
A. B.
C. D.
C
课堂练习
2.某天,某同学早上8点坐车从余姚图书馆出发去宁波大学,汽车离开余姚图书馆的距离(千米)与所用时间t(分)之间的函数关系如图所示.已知汽车在途中停车加油一次,则下列描述不正确的是( )
A.汽车在途中加油用了10分钟
B.若OA∥BC,则加满油以后的速度为80千米/小时
C.若汽车加油后的速度是90千米/小时,则a=25
D.该同学8:55到达宁波大学
C
课后练习
3.第一次“龟兔赛跑”,兔子因为在途中睡觉而输掉比赛,很不服气,决定与乌龟再比一次,并且骄傲地说,这次我一定不睡觉,让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛,则下列函数图象可以体现这次比赛过程的是( )
A. B.
C. D.
B
课后练习
4.如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒2个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为s,s关于t的函数图象如图②所示,当p运动到BC中点时,△PAD的面积为__________.
20
课后练习
5.星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(m)与散步所用时间t(min)之间的函数关系,依据图象,下面描述中符合小红散步情景的有_____(填序号)
①从家里出发,到了一个公共阅报栏,看了一会儿报后,继续向前走了一段然后回家了
②小红家距离公共阅报栏300m
③从家出发,一直散步(没有停留),然后回家了
④小红本次散步共用时18min
①②④
作 业
请完成课本P79页的练习题
19.1.2函数的图像
人教版八年级下册
第19章一次函数
19.1.2函数的图像
人教版八年级下册
第19章一次函数
01
了解函数图象的意义。
02
会根据函数图象分析函数的变化规律并解决具体问题。
教学目标
复习回顾
函数:
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
函数解析式:
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法,这种式子叫做函
数的解析式.
函数值:
对于自变量 x 在取值范围内的某个确定的值 a,函数 y 所对应的值为 b,即当 x=a 时,y=b,则 b 叫做当自变量的值为 a 时的函数值.
情景导入
生活中有很多函数关系难以列式子表示,通常用图像来直观地反映,例如用心电图表示心脏部位的生物电流与时间的关系。
这种表示函数的方法称为图象法
新知探究
即使对于能列式表示的函数关系,如果也能画图表示,那么会使函数关系更直观,例如正方形的面积。
如:正方形的边长为x,面积为S.
那么面积 S 随边长 x 变化的对应关系可表示为: S = x2 (x>0)
我们可以利用在坐标系中画函数图像的方法来表示S与x的关系吗?
新知探究
那么,什么是函数图象呢?
一般地, 对于一个 函数,如果把 与 的 分别作为点的 ,那么坐标平面内由这些 组成的图形,就是这个函数的图象.
自变量
函数
每对对应值
横、纵坐标
点
(自变量的取值,
相应的函数值)
纵坐标
横坐标
新知探究
画函数的步骤:
1.列表
x 0 0.5 1 1.5 2 2.5 3 3.5 4
S 0 0.25 1
2.25
4
6.25
9
12.25
16
新知探究
O
1
2
3
4
1
4
9
16
3.用光滑曲线去连接画出的点
表示x与S的对应关系的点有无数个,但是实际上我们只能描出其中有限个点,同时想象出其他点的位置。
x
S
2.描点
自变量
函数
函数图象
新知探究
因为该自变量 x 的取值范围是 x>0,所以(0,0)不在曲线上.
用空心圆表示不在曲线的点
用实心圆表示在曲线上的点
归纳总结
1.函数图象:
一般地, 对于一个 函数,如果把 与 的 分别作为点的 ,那么坐标平面内由这些 组成的图形,就是这个函数的图象.
自变量
函数
每对对应值
横、纵坐标
点
函数的图象可以是直线、射线、线段,也可以是曲线,甚至可以是一些不连续的点.
归纳总结
2.函数图象的画法步骤
1
列表:表中给出一些自变量的值及其对应的函数值.
2
描点:在直角坐标系中,以自变量的值为横坐标,相对应的函数值为纵坐标,描出表格中数值对应的各点.
3
连线:按照横坐标由小到大的顺序,把所描出的各点用平滑的曲线连接起来.
新知探究
思考:下图是自动测温仪记录的图象,它反映了北京的春季某天气温 T 如何随时间 t 的变化而变化.你从图象中得到了哪些信息?
可以认为,气温T是时间t的函数,上图就是这个函数图象.
4
14
24
8
0
-3
T/℃
t/时
新知探究
(1)这一天中 时气温最低,最低气温为 度, 时气温最高,最高气温为___度.
横轴表示自变量t(时间)
纵轴表示对应的函数T(温度)
最高点
最低点
4
-3
14
8
4
14
24
8
0
-3
T/℃
t/时
(2)从 时至 时气温呈下降状态(即温度随时间的增长而下降), 从 时到 时气温呈上升状态,从 时至 时气温又呈下降状态。
0
4
4
14
14
24
(3)我们可以从图像中看出这一天中任一时刻的气温大约是多少。
归纳总结
1.解答图象信息题主要运用数形结合思想,化图象信息为数字信息.
主要步骤如下:
1
了解横、纵轴的意义;
2
从 上判定函数与自变量的关系;
图象形状
3
抓住图象中端点,拐点等特殊点的实际意义.
新知应用
根据图象回答下列问题:
8
25
28
58
68
x/min
0.8
0.6
y/km
O
例2 小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.下图反映了这个过程中,小明离家的距离y与时间x 之间的对应关系.
新知应用
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
解:由纵坐标看出,食堂离小明家0.6km;由横坐标看出,小明从家到食堂用了8min.
小明离开家的时间
小明与家的距离
小明从家里出发
小明到达食堂
新知应用
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(2)小明吃早餐用了多少时间?
由横坐标看出,25-8=17,小明吃早餐用了 17min.
小明到达食堂
距离不变,说明小明停留在某个地方
小明离开食堂
新知探究
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
由纵坐标看出,0.8-0.6=0.2,食堂离图书馆0.2km;由横坐标看出,
28-25=3,小明从食堂到图书馆用了3min.
小明到达图书馆
小明离开食堂
新知探究
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(4)小明读报用了多少时间?
由横坐标看出,58-28=30,小明读报用了30min.
小明到达图书馆
小明离开图书馆
距离不变,说明小明停留在某个地方
新知应用
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
由纵坐标看出,图书馆离小明家0.8km;由横坐标看出, 68-58=10,小明从图书馆回家用了10min,由此算出平均速度是0.08km/min.
小明离开图书馆
小明回到家了
课堂总结
函数的图像
定义:如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
画法:一列表;二描点;三连线.
数形结合:了解横、纵轴的意义,从图像形状上判断函数与自变量的关系,抓住图像中端点,拐点等特殊点的实际意义。
课堂练习
1.下列各曲线中不能表示y是x的函数是( ).
A. B.
C. D.
C
课堂练习
2.某天,某同学早上8点坐车从余姚图书馆出发去宁波大学,汽车离开余姚图书馆的距离(千米)与所用时间t(分)之间的函数关系如图所示.已知汽车在途中停车加油一次,则下列描述不正确的是( )
A.汽车在途中加油用了10分钟
B.若OA∥BC,则加满油以后的速度为80千米/小时
C.若汽车加油后的速度是90千米/小时,则a=25
D.该同学8:55到达宁波大学
C
课后练习
3.第一次“龟兔赛跑”,兔子因为在途中睡觉而输掉比赛,很不服气,决定与乌龟再比一次,并且骄傲地说,这次我一定不睡觉,让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛,则下列函数图象可以体现这次比赛过程的是( )
A. B.
C. D.
B
课后练习
4.如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒2个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为s,s关于t的函数图象如图②所示,当p运动到BC中点时,△PAD的面积为__________.
20
课后练习
5.星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(m)与散步所用时间t(min)之间的函数关系,依据图象,下面描述中符合小红散步情景的有_____(填序号)
①从家里出发,到了一个公共阅报栏,看了一会儿报后,继续向前走了一段然后回家了
②小红家距离公共阅报栏300m
③从家出发,一直散步(没有停留),然后回家了
④小红本次散步共用时18min
①②④
作 业
请完成课本P79页的练习题
19.1.2函数的图像
人教版八年级下册
第19章一次函数
