2021-2022学年人教版数学七年级下册5.1.1相交线课件(16张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册5.1.1相交线课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 823.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
目标
任务一:明确本课时学习目标
1. 了解邻补角的定义与性质.
2. 了解对顶角的定义与性质.
任务二:对子讨论补角的定义与性质
who can say
承前
任务二:复习补角的定义与性质
1. (1)补角的定义:
如果两个角的和是——————,那么这两个角互为补角;
(2)补角的性质:
同角(或等角)的补角_______.
180°
相等
2. (1)已知∠1 =40°,则∠1的补角为_______;
(2)若∠1+∠2=180°,∠1+∠3=180°,则∠2与∠3的大小关系是_____,理由是_______________.
140°
相等
同角的补角相等
议一议
有一个公共点的两条直线形成相交直线.
请你画出任意两条相交直线.看看这四个角有什么关系
问题:两条相交直线.形成的小于平角的角有几个
任务三:学习教材第2页,补充概念、性质
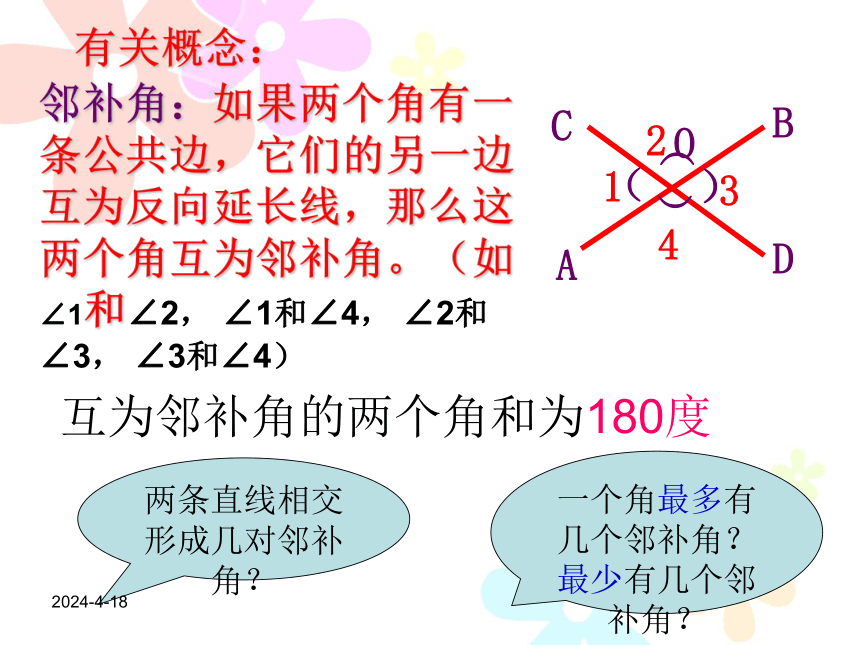
1. 邻补角:有一条_______,另一边互为__________的两个角互为邻补角.
邻补角的性质________________________________.
2. 对顶角:有一个__________,并且两边互为___________的两个角互为对顶角.对顶角的性质:____________.
公共边
反向延长线
一个角与它的邻补角的和等于180°
公共顶点
反向延长线
对顶角相等
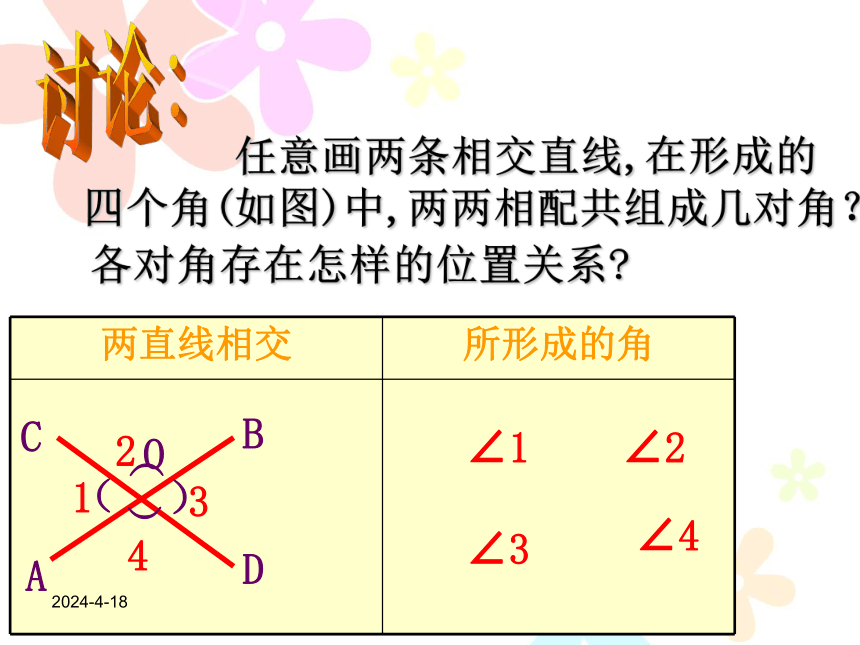
3. 观察图X5-1-1,回答下列问题.
图X5-1-1(1)____和___________,______和__________分别是一组邻补角,
∠1+∠2=_____,∠1+∠4=_______;
(2)_____和_____,_____和_____分别是一组对顶角,
∠1=______,∠2=_____.
∠4或∠2
∠1
∠2或∠4
∠3
180°
180°
∠4
∠1
∠3
∠2
∠3
∠4
任务四:例题学习
1. 如图X5-1-2,直线a,b相交.
图X5-1-2(1)若∠1=50°,则∠2=________,∠3=_____;
(2)若∠3=70°,则∠1=______,
∠2=______.
130°
50°
70°
110°
2. 如图X5-1-3,直线a,b相交,∠1=120°.求∠2,∠3,∠4的度数.
解:∠2=60°,
∠3=120°,
∠4=60°.
思考
任务五:
1. 邻补角与补角有什么异同之处?
2. 如何利用邻补角的性质证明对顶角的性质?
目标
任务一:明确本课时学习目标
1. 了解邻补角的定义与性质.
2. 了解对顶角的定义与性质.
任务二:对子讨论补角的定义与性质
who can say
承前
任务二:复习补角的定义与性质
1. (1)补角的定义:
如果两个角的和是——————,那么这两个角互为补角;
(2)补角的性质:
同角(或等角)的补角_______.
180°
相等
2. (1)已知∠1 =40°,则∠1的补角为_______;
(2)若∠1+∠2=180°,∠1+∠3=180°,则∠2与∠3的大小关系是_____,理由是_______________.
140°
相等
同角的补角相等
议一议
有一个公共点的两条直线形成相交直线.
请你画出任意两条相交直线.看看这四个角有什么关系
问题:两条相交直线.形成的小于平角的角有几个
任务三:学习教材第2页,补充概念、性质
1. 邻补角:有一条_______,另一边互为__________的两个角互为邻补角.
邻补角的性质________________________________.
2. 对顶角:有一个__________,并且两边互为___________的两个角互为对顶角.对顶角的性质:____________.
公共边
反向延长线
一个角与它的邻补角的和等于180°
公共顶点
反向延长线
对顶角相等
3. 观察图X5-1-1,回答下列问题.
图X5-1-1(1)____和___________,______和__________分别是一组邻补角,
∠1+∠2=_____,∠1+∠4=_______;
(2)_____和_____,_____和_____分别是一组对顶角,
∠1=______,∠2=_____.
∠4或∠2
∠1
∠2或∠4
∠3
180°
180°
∠4
∠1
∠3
∠2
∠3
∠4
任务四:例题学习
1. 如图X5-1-2,直线a,b相交.
图X5-1-2(1)若∠1=50°,则∠2=________,∠3=_____;
(2)若∠3=70°,则∠1=______,
∠2=______.
130°
50°
70°
110°
2. 如图X5-1-3,直线a,b相交,∠1=120°.求∠2,∠3,∠4的度数.
解:∠2=60°,
∠3=120°,
∠4=60°.
思考
任务五:
1. 邻补角与补角有什么异同之处?
2. 如何利用邻补角的性质证明对顶角的性质?
