华东师大版七上数学 2.6.1有理数的加法法则 课件(共32张PPT)
文档属性
| 名称 | 华东师大版七上数学 2.6.1有理数的加法法则 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 898.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
课前复习
1、一个不等于0的有理数可 看作由哪两 个部分组成?
(符号、绝对值)
2、比较下列各组数绝对值哪个大?
(1) -22与15; (2) 与
(3)2.7与- 3 .5
3、小学里学过什么数的加法运算?(举例说明)
(正数及零的加法运算)
(1)—22 (2) (3)—3.5
学习了有理数后,会有哪些加法运算?
(1)正数与正数 (2)正数与0
(3)正数与负数 (4)负数与负数
(5)负数与0
足球循环赛中,可以把进球数记为正数,失球数记为负数,它们的和叫做净胜球数。如果,红队进4个球,失2个球;白队进1个球,失1个球。
红队的净胜球数为:
(+4)+(-2)=
白队的净胜球数为:
(+1)+(-1)=
+2
0
讲授新课
课前复习
巩固练习
总结提高
2.6.1 有理数的加法
导入新课
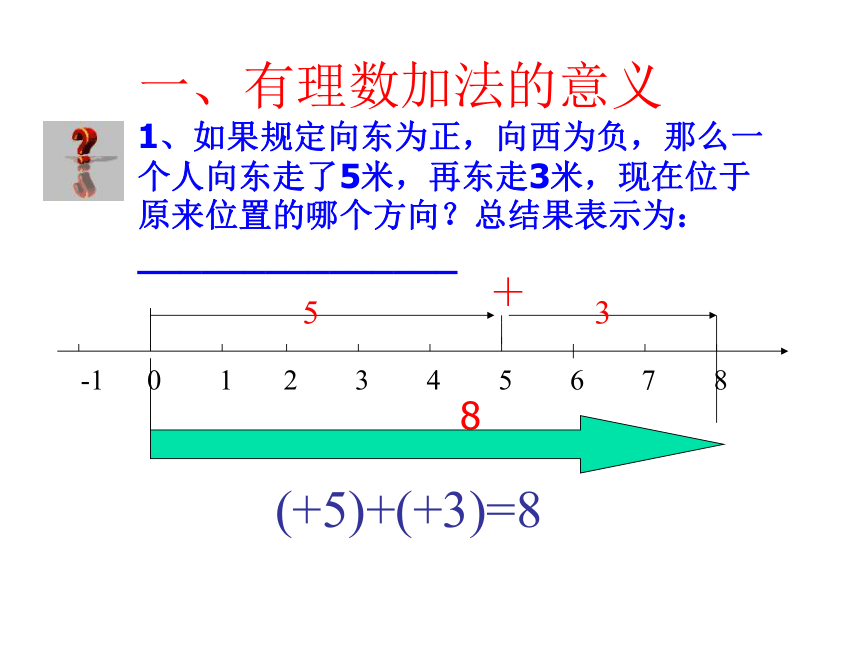
-1 0 1 2 3 4 5 6 7 8
(+5)+(+3)=8
5
3
+
8
一、有理数加法的意义
1、如果规定向东为正,向西为负,那么一个人向东走了5米,再东走3米,现在位于原来位置的哪个方向?总结果表示为:_______________
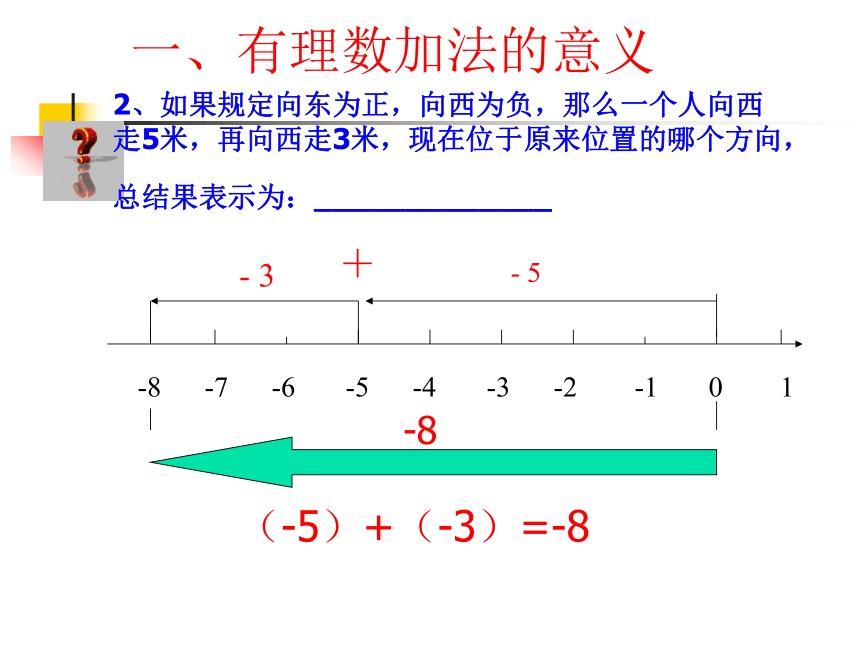
-8 -7 -6 -5 -4 -3 -2 -1 0 1
- 3
- 5
(-5)+(-3)=-8
+
-8
一、有理数加法的意义
2、如果规定向东为正,向西为负,那么一个人向西走5米,再向西走3米,现在位于原来位置的哪个方向,总结果表示为:_____________
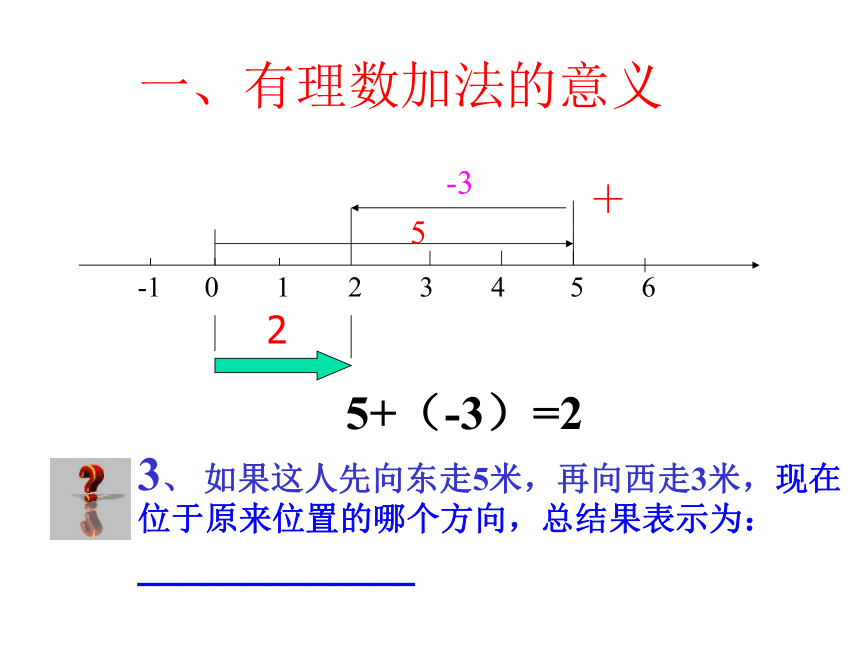
3、 如果这人先向东走5米,再向西走3米,现在位于原来位置的哪个方向,总结果表示为:_____________
5+(-3)=2
-1 0 1 2 3 4 5 6
5
-3
+
2
一、有理数加法的意义
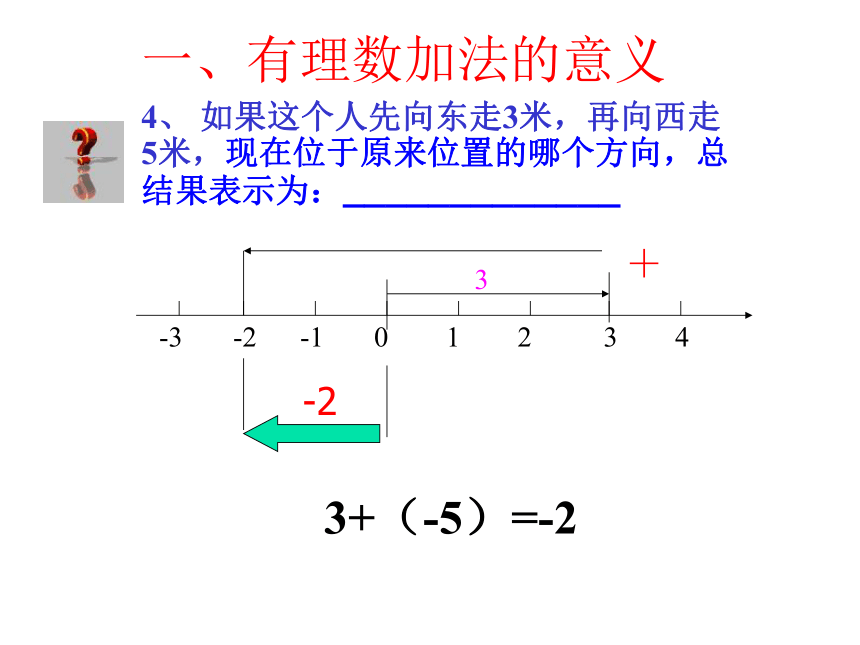
4、 如果这个人先向东走3米,再向西走5米,现在位于原来位置的哪个方向,总结果表示为:_____________
3+(-5)=-2
-3 -2 -1 0 1 2 3 4
3
+
-2
一、有理数加法的意义
5、向东走5米,再向西走5米,现在位于原来位置的哪个方向,总结果表示为:_____________
5+(-5)=0
-1 0 1 2 3 4 5 6
- 5
5
+
一、有理数加法的意义
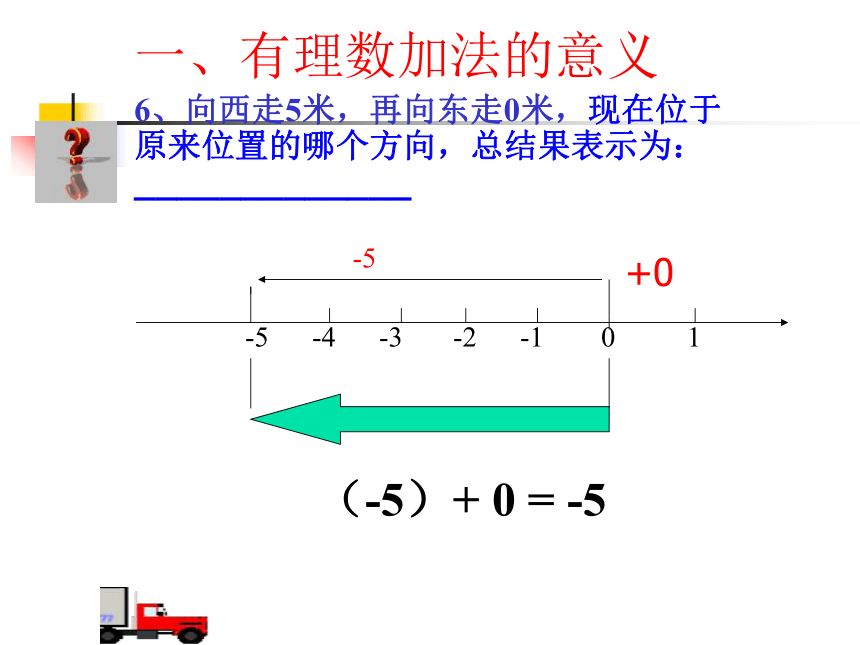
6、向西走5米,再向东走0米,现在位于原来位置的哪个方向,总结果表示为:_____________
(-5)+ 0 = -5
-5 -4 -3 -2 -1 0 1
-5
+0
一、有理数加法的意义
大家出题:(每人写一个有理数加法式子)
可以联系生活情景计算结果,还可以借助于
数轴求出总结果。
1. 5 + 3 = 8
2.(-5)+(-3)= - 8
3. 5+(-3)=2
4. 3+(-5)=-2
5. 5+(-5)=0
6.(-5)+0=-5
二、有理数加法的类型
同号两数相加
异号两数相加
一数和零相加
异号两数相加的特殊情况
( - 7 ) + (- 6 ) = - 13
( - 8 ) + (- 6 ) = - 14
(+ 5) + (+ 15) = + 20
(+9) + (+ 3) = + 12
从以下算式你能得出同号两数相加的法则吗?
并把绝对值相加
同号两数相加,取相同的符号,
这个符号是怎么来的呢?
(+ 5) + ( -3 ) = + 2
(+3) + ( -5 ) = - 2
( +5) + (- 9 ) = - 4
(- 11) + (+4 ) = - 7
并用较大的绝对值减去较小的绝对值.
异号两数相加,
从以下算式你能得出异号两数相加的法则吗?
这个符号是怎么来的呢?
取绝对值较大的加数的符号,
(+ 5) + ( -5 ) = 0
(-3) + ( +3 ) = 0
从以下算式你能得出什么法则呢?
互为相反数的两个数相加得0;
一个数同0相加,仍得这个数.
( +5) + 0 = +5
0 + (-4 ) = - 4
1、 同号两数相加,取相同的符号,并把绝对值相加。
2、 绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
3、互为相反数 的两个数相加得0。
4、 一个数同0相加,仍得这个数。
三、有理数加法法则
注意:1、确定和的符号;
2、确定和的绝对值。
四、有理数的加法运算
例一:
1、(-4)+(-5 )
=-( ) (取相同的符号)
=-(4 + 5) (把绝对值相加)
=- 9
(同号两数相加)
2、( -6) + 2
(绝对值不相等的异号两数相加)
(取绝对值较大的加数符号)
(用较大的绝对值减去较小的绝对值)
=-( )
=- 4
=-(6 – 2 )
运算步骤
再确定和的符号;
后进行绝对值的加减运算
先判断类型 (同号、异号等);
(1) (-3)+(-9)
(2) (-1/2)+(+1/3)
(3) 0 +( -0﹒1 )
例二: 计算
解:(1)(-3)+ (-9) (3) 0 +( -0﹒1 )
=-(3+9) = -0﹒1
=-12
(2)(-1/2)+(+1/3)
=-(1/2-1/3)
=-1/6
计算:
例题2
请注意书写格式!
一 、接力口答:
1、 (+4)+(-7)
2、 (-8)+(-3)
3、 (-9)+(+5)
4、 (-6)+(+6)
5、 (-7)+0
6、 8+(-1)
7、 (-7)+1
8、 0+(-10)
巩固练习
1、 -3
2、 -11
3、 -4
4、 0
5、 -7
6、 7
7、 -6
8、-10
二、计算:
(1)15+(-22)
(2)(-13)+(-8)
(3)(-0.9)+1.5
(4)2.7+(-3.5)
(5)1/2+(-2/3)
(6)(-1/4)+(-1/4)
巩固练习
( -7 )
( -21 )
( 0.6 )
( -0.8)
(1/6)
( -1/2)
小结
1、掌握有理数的加法法则,正确地进行加法运算。
2、两个有理数相加,首先判断加法类型,再确定和的符号,最后确定和的绝对值。
3、注意异号绝对值
不等的两数相加。
总结提高
同号两数相加,取相同的符号,并把绝对值相加。
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。互为相反数 的两个数相加得0。
一个数同0相加,仍得这个数。
异号绝对值不等的两数相加,分步思考:
①确定和的符号;
②确定和的
绝对值,写出所得和;
③相反数相加直接得出零。
注意:
思考题
1、判断题:
(1)两个负数的和一定是负数;
(2)绝对值相等的两个数的和等于零
(3)若两个有理数相加时的和为负数,
这两个有理数一定是负数;
(4)若两个有理数相加时的和为正数,
这两个有理数一定都是正数。
2、已知|a|=8,|b|=2;
(1)当a,b同号时,求a+b的值
(2)当a,b异号时,求a+b的值。
思考题
课外练习:教科书P34习题2.6第1、2题
再见!
课前复习
1、一个不等于0的有理数可 看作由哪两 个部分组成?
(符号、绝对值)
2、比较下列各组数绝对值哪个大?
(1) -22与15; (2) 与
(3)2.7与- 3 .5
3、小学里学过什么数的加法运算?(举例说明)
(正数及零的加法运算)
(1)—22 (2) (3)—3.5
学习了有理数后,会有哪些加法运算?
(1)正数与正数 (2)正数与0
(3)正数与负数 (4)负数与负数
(5)负数与0
足球循环赛中,可以把进球数记为正数,失球数记为负数,它们的和叫做净胜球数。如果,红队进4个球,失2个球;白队进1个球,失1个球。
红队的净胜球数为:
(+4)+(-2)=
白队的净胜球数为:
(+1)+(-1)=
+2
0
讲授新课
课前复习
巩固练习
总结提高
2.6.1 有理数的加法
导入新课
-1 0 1 2 3 4 5 6 7 8
(+5)+(+3)=8
5
3
+
8
一、有理数加法的意义
1、如果规定向东为正,向西为负,那么一个人向东走了5米,再东走3米,现在位于原来位置的哪个方向?总结果表示为:_______________
-8 -7 -6 -5 -4 -3 -2 -1 0 1
- 3
- 5
(-5)+(-3)=-8
+
-8
一、有理数加法的意义
2、如果规定向东为正,向西为负,那么一个人向西走5米,再向西走3米,现在位于原来位置的哪个方向,总结果表示为:_____________
3、 如果这人先向东走5米,再向西走3米,现在位于原来位置的哪个方向,总结果表示为:_____________
5+(-3)=2
-1 0 1 2 3 4 5 6
5
-3
+
2
一、有理数加法的意义
4、 如果这个人先向东走3米,再向西走5米,现在位于原来位置的哪个方向,总结果表示为:_____________
3+(-5)=-2
-3 -2 -1 0 1 2 3 4
3
+
-2
一、有理数加法的意义
5、向东走5米,再向西走5米,现在位于原来位置的哪个方向,总结果表示为:_____________
5+(-5)=0
-1 0 1 2 3 4 5 6
- 5
5
+
一、有理数加法的意义
6、向西走5米,再向东走0米,现在位于原来位置的哪个方向,总结果表示为:_____________
(-5)+ 0 = -5
-5 -4 -3 -2 -1 0 1
-5
+0
一、有理数加法的意义
大家出题:(每人写一个有理数加法式子)
可以联系生活情景计算结果,还可以借助于
数轴求出总结果。
1. 5 + 3 = 8
2.(-5)+(-3)= - 8
3. 5+(-3)=2
4. 3+(-5)=-2
5. 5+(-5)=0
6.(-5)+0=-5
二、有理数加法的类型
同号两数相加
异号两数相加
一数和零相加
异号两数相加的特殊情况
( - 7 ) + (- 6 ) = - 13
( - 8 ) + (- 6 ) = - 14
(+ 5) + (+ 15) = + 20
(+9) + (+ 3) = + 12
从以下算式你能得出同号两数相加的法则吗?
并把绝对值相加
同号两数相加,取相同的符号,
这个符号是怎么来的呢?
(+ 5) + ( -3 ) = + 2
(+3) + ( -5 ) = - 2
( +5) + (- 9 ) = - 4
(- 11) + (+4 ) = - 7
并用较大的绝对值减去较小的绝对值.
异号两数相加,
从以下算式你能得出异号两数相加的法则吗?
这个符号是怎么来的呢?
取绝对值较大的加数的符号,
(+ 5) + ( -5 ) = 0
(-3) + ( +3 ) = 0
从以下算式你能得出什么法则呢?
互为相反数的两个数相加得0;
一个数同0相加,仍得这个数.
( +5) + 0 = +5
0 + (-4 ) = - 4
1、 同号两数相加,取相同的符号,并把绝对值相加。
2、 绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
3、互为相反数 的两个数相加得0。
4、 一个数同0相加,仍得这个数。
三、有理数加法法则
注意:1、确定和的符号;
2、确定和的绝对值。
四、有理数的加法运算
例一:
1、(-4)+(-5 )
=-( ) (取相同的符号)
=-(4 + 5) (把绝对值相加)
=- 9
(同号两数相加)
2、( -6) + 2
(绝对值不相等的异号两数相加)
(取绝对值较大的加数符号)
(用较大的绝对值减去较小的绝对值)
=-( )
=- 4
=-(6 – 2 )
运算步骤
再确定和的符号;
后进行绝对值的加减运算
先判断类型 (同号、异号等);
(1) (-3)+(-9)
(2) (-1/2)+(+1/3)
(3) 0 +( -0﹒1 )
例二: 计算
解:(1)(-3)+ (-9) (3) 0 +( -0﹒1 )
=-(3+9) = -0﹒1
=-12
(2)(-1/2)+(+1/3)
=-(1/2-1/3)
=-1/6
计算:
例题2
请注意书写格式!
一 、接力口答:
1、 (+4)+(-7)
2、 (-8)+(-3)
3、 (-9)+(+5)
4、 (-6)+(+6)
5、 (-7)+0
6、 8+(-1)
7、 (-7)+1
8、 0+(-10)
巩固练习
1、 -3
2、 -11
3、 -4
4、 0
5、 -7
6、 7
7、 -6
8、-10
二、计算:
(1)15+(-22)
(2)(-13)+(-8)
(3)(-0.9)+1.5
(4)2.7+(-3.5)
(5)1/2+(-2/3)
(6)(-1/4)+(-1/4)
巩固练习
( -7 )
( -21 )
( 0.6 )
( -0.8)
(1/6)
( -1/2)
小结
1、掌握有理数的加法法则,正确地进行加法运算。
2、两个有理数相加,首先判断加法类型,再确定和的符号,最后确定和的绝对值。
3、注意异号绝对值
不等的两数相加。
总结提高
同号两数相加,取相同的符号,并把绝对值相加。
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。互为相反数 的两个数相加得0。
一个数同0相加,仍得这个数。
异号绝对值不等的两数相加,分步思考:
①确定和的符号;
②确定和的
绝对值,写出所得和;
③相反数相加直接得出零。
注意:
思考题
1、判断题:
(1)两个负数的和一定是负数;
(2)绝对值相等的两个数的和等于零
(3)若两个有理数相加时的和为负数,
这两个有理数一定是负数;
(4)若两个有理数相加时的和为正数,
这两个有理数一定都是正数。
2、已知|a|=8,|b|=2;
(1)当a,b同号时,求a+b的值
(2)当a,b异号时,求a+b的值。
思考题
课外练习:教科书P34习题2.6第1、2题
再见!
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
