华东师大版七上数学 4.3立体图形的表面展开图 课件(共14张PPT)
文档属性
| 名称 | 华东师大版七上数学 4.3立体图形的表面展开图 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 280.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 20:56:33 | ||
图片预览



文档简介
(共14张PPT)
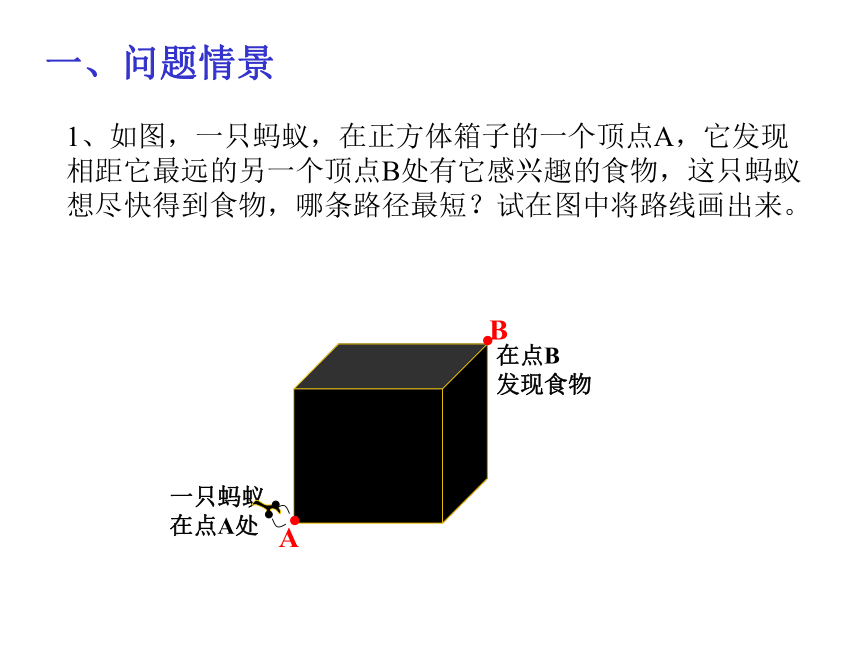
1、如图,一只蚂蚁,在正方体箱子的一个顶点A,它发现相距它最远的另一个顶点B处有它感兴趣的食物,这只蚂蚁想尽快得到食物,哪条路径最短?试在图中将路线画出来。
一、问题情景
.
一只蚂蚁
在点A处
A
B
在点B
发现食物
.
2、怎样用平面图形围成立体图形?
(1)同学们看我手里拿着这张长方形的纸,把它卷起来(把长方形的短边卷一下,并使两条长边靠拢),大家看得到是什么立体图形?还可以换一个方向卷一个吗?
(2)做一做:给2个大小一样的圆纸片和一条长方形的纸带,用透明胶粘成一个立体图形,怎么粘?(长方形的长大于圆的周长)。
思考:圆锥的侧面展开图是什么?
扇形
粘成
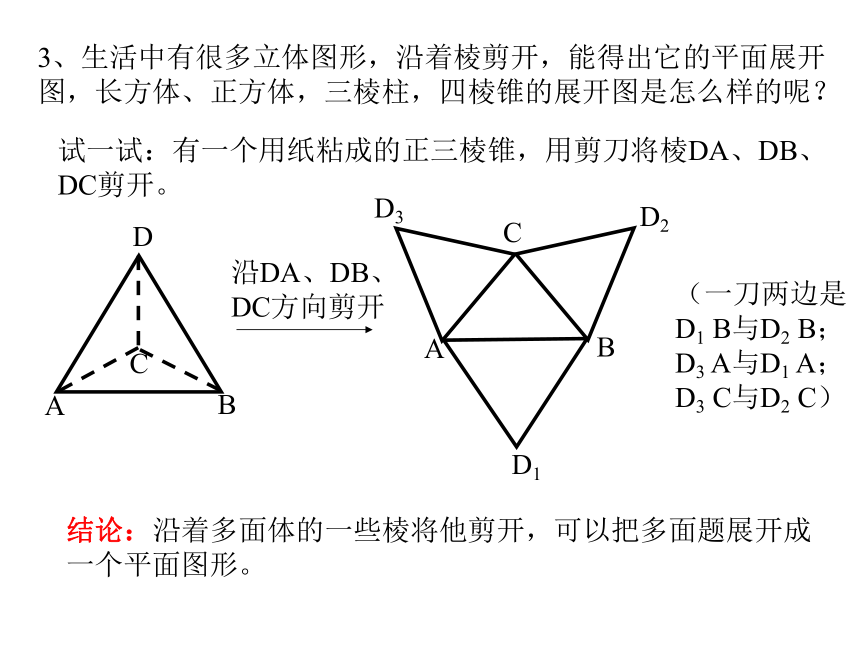
3、生活中有很多立体图形,沿着棱剪开,能得出它的平面展开图,长方体、正方体,三棱柱,四棱锥的展开图是怎么样的呢?
试一试:有一个用纸粘成的正三棱锥,用剪刀将棱DA、DB、DC剪开。
A
B
D
C
沿DA、DB、DC方向剪开
A
C
B
D3
D2
D1
(一刀两边是D1 B与D2 B; D3 A与D1 A; D3 C与D2 C)
结论:沿着多面体的一些棱将他剪开,可以把多面题展开成一个平面图形。
二、实例探究与交流:
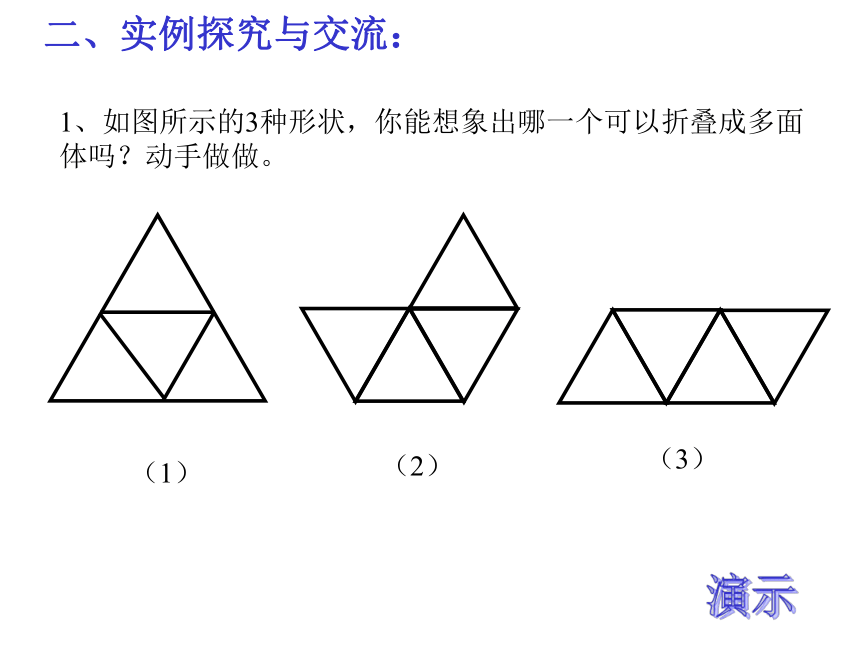
1、如图所示的3种形状,你能想象出哪一个可以折叠成多面体吗?动手做做。
(1)
(2)
(3)
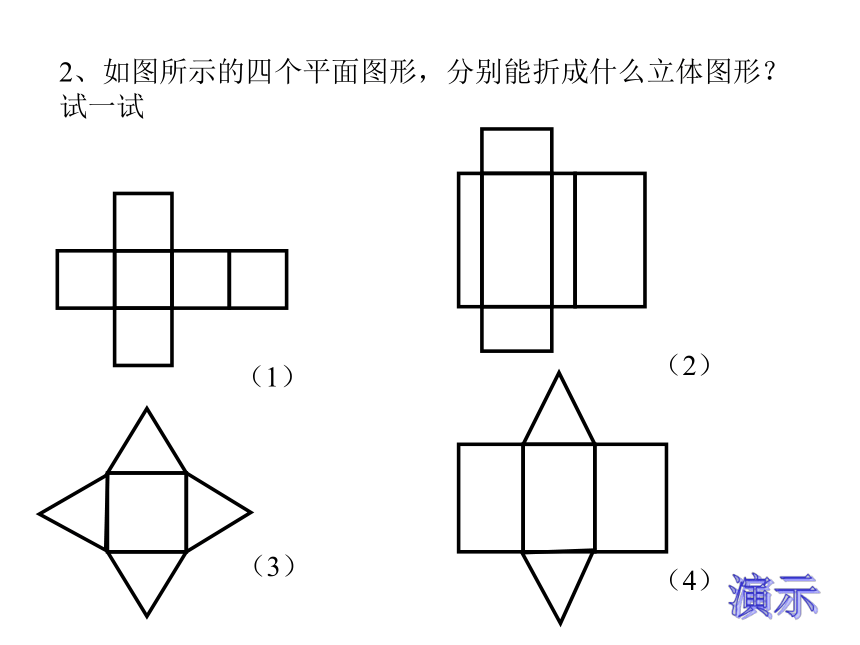
2、如图所示的四个平面图形,分别能折成什么立体图形?试一试
(4)
(1)
(3)
(2)
多面体的展开图可以用不同方法折叠成立体图形。常用的方法有下面两种:
(1)粘合拼凑法:找展开图外周长上公共棱边,设想用胶水粘上,看能否围成立体图形。
(2)方位法:把有规则的平面展开图先定出上面、下面、前面、左面、右面。从六个方位来思考,对长方体、正方体展开图应用比较多。
3、如图所示的六个平面图形都是正方体的展开图吗?动手折折看。
思考:你还能画出与上面不一样的正方体的展开图吗?
结论:同一个立体图形,按不同的方式展开得到的平面展开图是不一样的
(1)
(2)
(3)
(4)
(5)
(6)
如图,一只蚂蚁,在正方体箱子的一个顶点A,它发现相距它最远的另一个顶点B处有它感兴趣的食物,这只蚂蚁想尽快得到食物,哪条路径最短?试在图中将路线画出来。
.
一只蚂蚁
在点A处
A
B
在点B
发现食物
.
A
B1
B2
.
.
.
三、进一步探究交流:
1、如图是某多面体的平面展开图,指出它们的名称。
分析:左边的平面展开图,把C1 、 C2 、 C3 、 C4 、 C5 和拼成一点,得到的是五棱锥,右边按共棱粘和方法可得到立体图形是三棱柱。
解:(1)五棱锥 (2)三棱柱
方法总结: ①侧面是三角形,底面是五边形,所以是五棱锥;
②侧面是长方形,底面是三角形,所以是三棱柱 。
(1)
(2)
2、如图不是正方体的平面展开图是( )
分析:用方位拼凑法思考得到答案为A
方法总结:①用方位拼凑法,B、C、D都能拼成正方体;
②一般地有田字格的不是正方体的平面展开图;
③正方体展开图,外周长必须是小正方形边长的14倍,简称14个单位,因为正方体剪开必须剪7刀,1刀两边,由此得出14。
A
B
C
D
四、拓展应用创新:
1、建新的茶杯是圆柱形,如图是茶杯的截面图,左边下方有一只蚂蚁,从A处爬行到对面的中点B处,如果蚂蚁爬行路线最短,请画出这条最短路线图。
(点拨:画出圆柱形茶杯的侧面展开图,连接A、B两点)
解:如图所示:AB是爬行路线
●
●
A
B
A●
● B
2、把立方体的六个面分别涂上六种不同颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况列表如下:
现将上述大小相同,颜色、花朵分布也完全相同的四个立方体拼成一个水平放置的长方体,如图所示。问长方体的下底面共有多少朵花
颜色
花的朵数
红
黄
蓝
白
紫
绿
1
2
3
4
5
6
黄
紫
红
蓝
白
红
白
黄
红
五、课堂小节
展开
1、立体图形
平面图形
折叠
2、立体图形与平面图形相互变换的方法:
(1)粘合拼凑法;
(2)方位法。
1、如图,一只蚂蚁,在正方体箱子的一个顶点A,它发现相距它最远的另一个顶点B处有它感兴趣的食物,这只蚂蚁想尽快得到食物,哪条路径最短?试在图中将路线画出来。
一、问题情景
.
一只蚂蚁
在点A处
A
B
在点B
发现食物
.
2、怎样用平面图形围成立体图形?
(1)同学们看我手里拿着这张长方形的纸,把它卷起来(把长方形的短边卷一下,并使两条长边靠拢),大家看得到是什么立体图形?还可以换一个方向卷一个吗?
(2)做一做:给2个大小一样的圆纸片和一条长方形的纸带,用透明胶粘成一个立体图形,怎么粘?(长方形的长大于圆的周长)。
思考:圆锥的侧面展开图是什么?
扇形
粘成
3、生活中有很多立体图形,沿着棱剪开,能得出它的平面展开图,长方体、正方体,三棱柱,四棱锥的展开图是怎么样的呢?
试一试:有一个用纸粘成的正三棱锥,用剪刀将棱DA、DB、DC剪开。
A
B
D
C
沿DA、DB、DC方向剪开
A
C
B
D3
D2
D1
(一刀两边是D1 B与D2 B; D3 A与D1 A; D3 C与D2 C)
结论:沿着多面体的一些棱将他剪开,可以把多面题展开成一个平面图形。
二、实例探究与交流:
1、如图所示的3种形状,你能想象出哪一个可以折叠成多面体吗?动手做做。
(1)
(2)
(3)
2、如图所示的四个平面图形,分别能折成什么立体图形?试一试
(4)
(1)
(3)
(2)
多面体的展开图可以用不同方法折叠成立体图形。常用的方法有下面两种:
(1)粘合拼凑法:找展开图外周长上公共棱边,设想用胶水粘上,看能否围成立体图形。
(2)方位法:把有规则的平面展开图先定出上面、下面、前面、左面、右面。从六个方位来思考,对长方体、正方体展开图应用比较多。
3、如图所示的六个平面图形都是正方体的展开图吗?动手折折看。
思考:你还能画出与上面不一样的正方体的展开图吗?
结论:同一个立体图形,按不同的方式展开得到的平面展开图是不一样的
(1)
(2)
(3)
(4)
(5)
(6)
如图,一只蚂蚁,在正方体箱子的一个顶点A,它发现相距它最远的另一个顶点B处有它感兴趣的食物,这只蚂蚁想尽快得到食物,哪条路径最短?试在图中将路线画出来。
.
一只蚂蚁
在点A处
A
B
在点B
发现食物
.
A
B1
B2
.
.
.
三、进一步探究交流:
1、如图是某多面体的平面展开图,指出它们的名称。
分析:左边的平面展开图,把C1 、 C2 、 C3 、 C4 、 C5 和拼成一点,得到的是五棱锥,右边按共棱粘和方法可得到立体图形是三棱柱。
解:(1)五棱锥 (2)三棱柱
方法总结: ①侧面是三角形,底面是五边形,所以是五棱锥;
②侧面是长方形,底面是三角形,所以是三棱柱 。
(1)
(2)
2、如图不是正方体的平面展开图是( )
分析:用方位拼凑法思考得到答案为A
方法总结:①用方位拼凑法,B、C、D都能拼成正方体;
②一般地有田字格的不是正方体的平面展开图;
③正方体展开图,外周长必须是小正方形边长的14倍,简称14个单位,因为正方体剪开必须剪7刀,1刀两边,由此得出14。
A
B
C
D
四、拓展应用创新:
1、建新的茶杯是圆柱形,如图是茶杯的截面图,左边下方有一只蚂蚁,从A处爬行到对面的中点B处,如果蚂蚁爬行路线最短,请画出这条最短路线图。
(点拨:画出圆柱形茶杯的侧面展开图,连接A、B两点)
解:如图所示:AB是爬行路线
●
●
A
B
A●
● B
2、把立方体的六个面分别涂上六种不同颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况列表如下:
现将上述大小相同,颜色、花朵分布也完全相同的四个立方体拼成一个水平放置的长方体,如图所示。问长方体的下底面共有多少朵花
颜色
花的朵数
红
黄
蓝
白
紫
绿
1
2
3
4
5
6
黄
紫
红
蓝
白
红
白
黄
红
五、课堂小节
展开
1、立体图形
平面图形
折叠
2、立体图形与平面图形相互变换的方法:
(1)粘合拼凑法;
(2)方位法。
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
