2.1.3-2.1.4空间直线与平面.平面与平面的位置关系
文档属性
| 名称 | 2.1.3-2.1.4空间直线与平面.平面与平面的位置关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 249.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-03 20:25:24 | ||
图片预览






文档简介
课件22张PPT。2.1.3《空间中直线与平面之间的位置关系》2.1.4《空间中平面与平面之间的位置关系》湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作复习引入:1、空间两直线的位置关系(1)相交;(2)平行;(3)异面2.公理4的内容是什么?平行于同一条直线的两条直线互相平行.3.等角定理的内容是什么?空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。(同向相等)4.什么是异面直线?什么是异面直线所成的角?
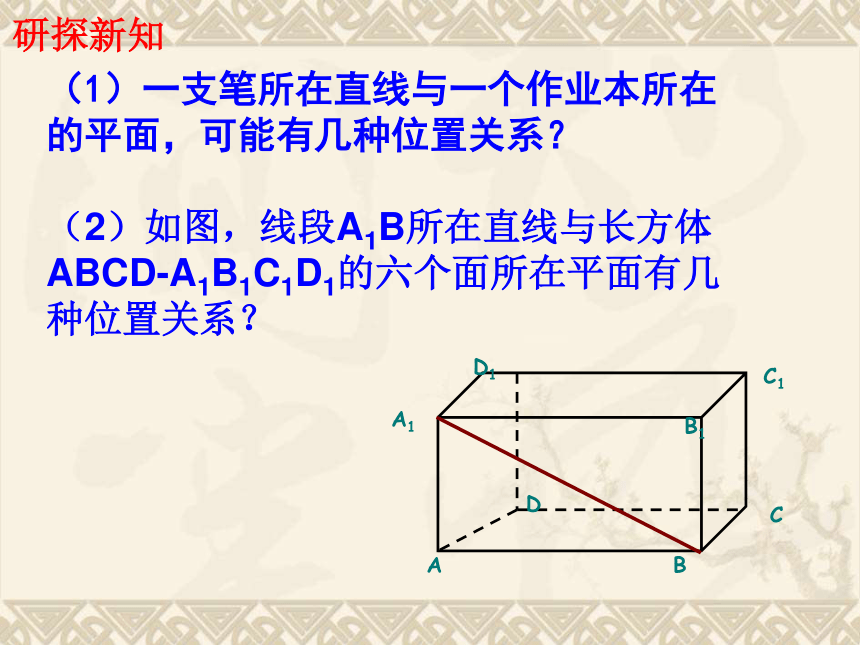
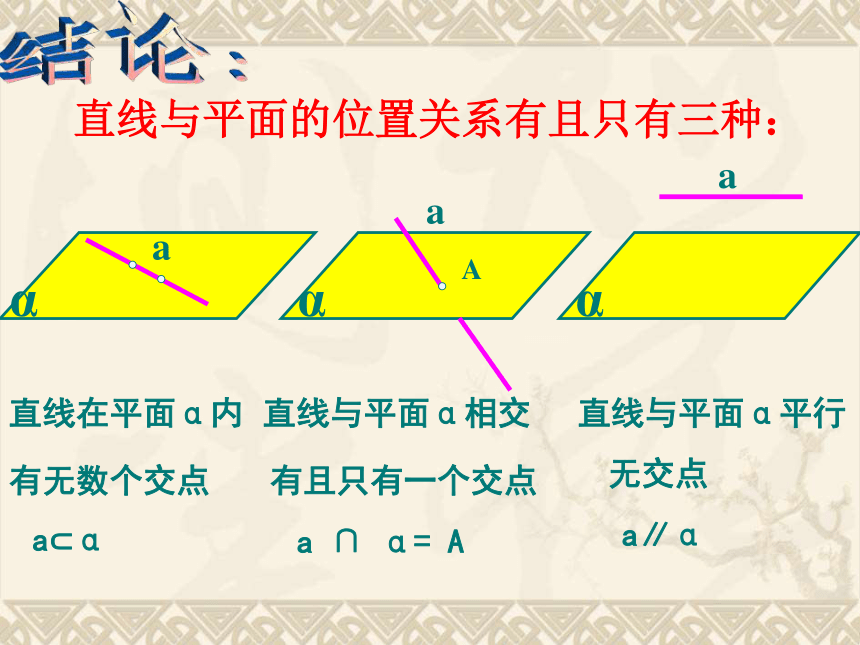
什么是异面直线垂直?研探新知(1)一支笔所在直线与一个作业本所在的平面,可能有几种位置关系?(2)如图,线段A1B所在直线与长方体ABCD-A1B1C1D1的六个面所在平面有几种位置关系?直线与平面α相交 直线与平面α平行a∥α 无交点直线在平面α内有无数个交点a?α a ∩ α= A有且只有一个交点 结论:直线与平面的位置关系有且只有三种:分析:可以借助长方体模型来看上述问题是否正确。
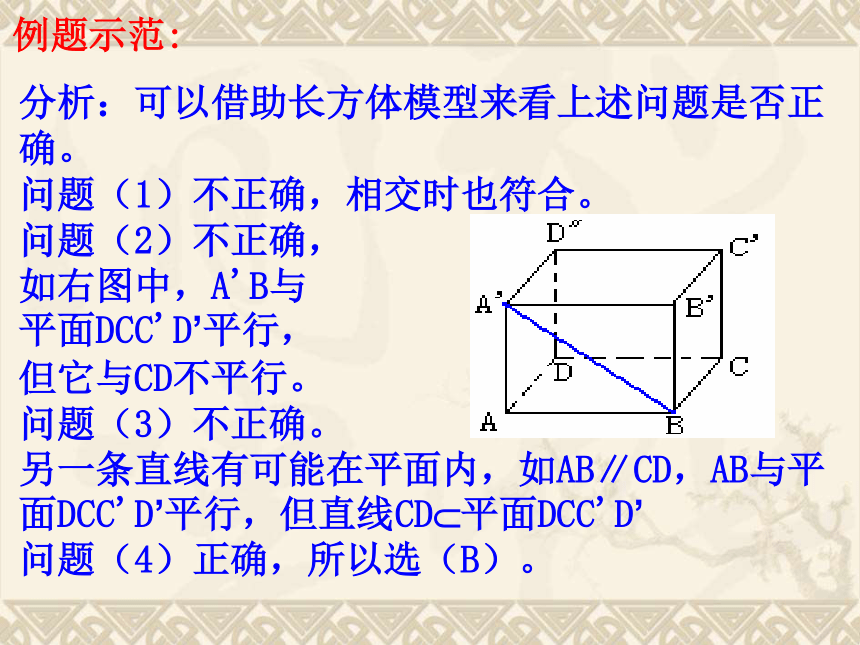
问题(1)不正确,相交时也符合。
问题(2)不正确,
如右图中,A'B与
平面DCC'D’平行,
但它与CD不平行。
问题(3)不正确。
另一条直线有可能在平面内,如AB∥CD,AB与平面DCC'D’平行,但直线CDì平面DCC'D’
问题(4)正确,所以选(B)。例题示范:例2?已知直线a在平面α外,则 (???)
(A)a∥α??? ?(B)直线a与平面α至少有一个公共点 (C)a?α=A
(D)直线a与平面α至多有一个公共点。例题示范:D巩固练习:?1.选择题
(1)以下命题(其中a,b表示直线,a表示平面)
①若a∥b,bìa,则a∥a???②若a∥a,b∥a,则a∥b ③若a∥b,b∥a,则a∥a???④若a∥a,bìa,则a∥b 其中正确命题的个数是 ( )(A)0个 (B)1个 (C)2个 (D)3个A2.已知a∥a,b∥a,则直线a,b的位置关系
①平行;②垂直不相交;③垂直相交;
④相交;⑤不垂直且不相交.??
其中可能成立的有 (???)
(A)2个 (B)3个 (C)4个 (D)5个
3.如果平面a外有两点A、B,它们到平面a的距离都是a,则直线AB和平面a的位置关系一定是(???)
(A)平行 (B)相交???
(C)平行或相交??(D)AB ìa巩固练习:?DC巩固练习:?4.已知m,n为异面直线,m∥平面a,n∥平面b,a∩b=l,则l (???)
(A)与m,n都相交??????
(B)与m,n中至少一条相交
(C)与m,n都不相交???
(D)与m,n中一条相交C1、空间中两条直线有几种位置关系?分别是什么?(1)相交;(2)平行;(3)异面2、直线与平面有几种位置关系?分别是什么?(1)直线在平面内——有无数个公共点:?
(2)直线与平面相交——有且只有一个公共点;?
(3)直线与平面平行——没有公共点;
其中直线与平面相交或平行的情况统称为直线
在平面外.研探新知:提出问题:空间中平面与平面的位置关系又是怎 样的呢?观察思考:(1)拿出两本书,看作两个平面,上下、左右移动和翻转,它们之间的位置关系有几种?(2)如图,围成长方体AC’的六个面,两两之间的位置关系有几种?
在问题(1)中,通过观察可以发现,两本书可以平行,也可以是相交,注意平面是无限延展的。
在问题(2)中上下面,左右面,前后面是平行的,相邻的两个面是相交的,所以位置关系有平行与相交两种。结论: 两个平面之间的关系有且只有两种:
(1)两个平面平行――没有公共点;
(2)两个平面相交――有一条公共直线。结论:想一想:两个平面平行应怎样画?相交又怎样画?画两个互相平行的平面时,要注意使表示
平面的两个平行四边形的对应边平行图1图2×√两个平面的位置关系两平面平行没有公共点有一条公共直线两平面相交α∥βα∩β=a探究:1.已知平面α,β,直线a,b,且α∥β,aìα,?bìβ,则直线a与直线b具有什么样的位置关系? 答:没有交点,有可能平行,有可能是异面直线。2.直线与直线,直线与平面,平面与平面之间没有公共点就平行,平行就没有公共点,这句话对吗?为什么?3.直线与直线,直线与平面,平面与平面之间有两个公共点时,它们的位置关系如何?4.如果平面与平面有三个公共点时位置关系如何?练习巩固:1.如果三个平面两两相交,那么它们的交线有多少条?画出图形表示你的结论。答:有可能1条,也有可能3条交线。(1)(2)2.平面α//平面β,且aìα,下列四个命题:
A、a与β内的所有直线平行??????????????????
B、a与β内的无数条直线平行???????????????
C、a与β内的任一直线都不垂直?????????????
D、a与β无公共点??????????????????????????其中假命题为(????)练习巩固:例. 下列命题中正确的个数是
①若直线l上有无数个点不在平面?内,
则l∥?.
②若直线l与平面?平行,则l与平面?内
的任意一条直线都平行.
③如果两条平行直线中的一条与一个平
面平行,那么另一条也与这个平面平行.
④若直线l与平面?平行,则l与平面?内
的任意一条直线都没有公共点.A. 0 B. 1 C. 2 D. 3切割长方体一个长方体切一刀可以分成多少块?
一个长方体切两刀可以分成多少块?
一个长方体切三刀可以分成多少块?
23或44或6或7或8课堂讨论一个长方体切三刀可以分成多少块?练习巩固:(2)(3)(4)(5)466781、空间中两条直线有几种位置关系?分别是什么?(1)相交;(2)平行;(3)异面2、直线与平面有几种位置关系?分别是什么?(1)直线在平面内——有无数个公共点:?
(2)直线与平面相交——有且只有一个公共点;?
(3)直线与平面平行——没有公共点;
其中直线与平面相交或平行的情况统称为直线
在平面外.3.平面之间的关系有几种?(1)两个平面平行――没有公共点;
(2)两个平面相交――有一条公共直线。小结下课
什么是异面直线垂直?研探新知(1)一支笔所在直线与一个作业本所在的平面,可能有几种位置关系?(2)如图,线段A1B所在直线与长方体ABCD-A1B1C1D1的六个面所在平面有几种位置关系?直线与平面α相交 直线与平面α平行a∥α 无交点直线在平面α内有无数个交点a?α a ∩ α= A有且只有一个交点 结论:直线与平面的位置关系有且只有三种:分析:可以借助长方体模型来看上述问题是否正确。
问题(1)不正确,相交时也符合。
问题(2)不正确,
如右图中,A'B与
平面DCC'D’平行,
但它与CD不平行。
问题(3)不正确。
另一条直线有可能在平面内,如AB∥CD,AB与平面DCC'D’平行,但直线CDì平面DCC'D’
问题(4)正确,所以选(B)。例题示范:例2?已知直线a在平面α外,则 (???)
(A)a∥α??? ?(B)直线a与平面α至少有一个公共点 (C)a?α=A
(D)直线a与平面α至多有一个公共点。例题示范:D巩固练习:?1.选择题
(1)以下命题(其中a,b表示直线,a表示平面)
①若a∥b,bìa,则a∥a???②若a∥a,b∥a,则a∥b ③若a∥b,b∥a,则a∥a???④若a∥a,bìa,则a∥b 其中正确命题的个数是 ( )(A)0个 (B)1个 (C)2个 (D)3个A2.已知a∥a,b∥a,则直线a,b的位置关系
①平行;②垂直不相交;③垂直相交;
④相交;⑤不垂直且不相交.??
其中可能成立的有 (???)
(A)2个 (B)3个 (C)4个 (D)5个
3.如果平面a外有两点A、B,它们到平面a的距离都是a,则直线AB和平面a的位置关系一定是(???)
(A)平行 (B)相交???
(C)平行或相交??(D)AB ìa巩固练习:?DC巩固练习:?4.已知m,n为异面直线,m∥平面a,n∥平面b,a∩b=l,则l (???)
(A)与m,n都相交??????
(B)与m,n中至少一条相交
(C)与m,n都不相交???
(D)与m,n中一条相交C1、空间中两条直线有几种位置关系?分别是什么?(1)相交;(2)平行;(3)异面2、直线与平面有几种位置关系?分别是什么?(1)直线在平面内——有无数个公共点:?
(2)直线与平面相交——有且只有一个公共点;?
(3)直线与平面平行——没有公共点;
其中直线与平面相交或平行的情况统称为直线
在平面外.研探新知:提出问题:空间中平面与平面的位置关系又是怎 样的呢?观察思考:(1)拿出两本书,看作两个平面,上下、左右移动和翻转,它们之间的位置关系有几种?(2)如图,围成长方体AC’的六个面,两两之间的位置关系有几种?
在问题(1)中,通过观察可以发现,两本书可以平行,也可以是相交,注意平面是无限延展的。
在问题(2)中上下面,左右面,前后面是平行的,相邻的两个面是相交的,所以位置关系有平行与相交两种。结论: 两个平面之间的关系有且只有两种:
(1)两个平面平行――没有公共点;
(2)两个平面相交――有一条公共直线。结论:想一想:两个平面平行应怎样画?相交又怎样画?画两个互相平行的平面时,要注意使表示
平面的两个平行四边形的对应边平行图1图2×√两个平面的位置关系两平面平行没有公共点有一条公共直线两平面相交α∥βα∩β=a探究:1.已知平面α,β,直线a,b,且α∥β,aìα,?bìβ,则直线a与直线b具有什么样的位置关系? 答:没有交点,有可能平行,有可能是异面直线。2.直线与直线,直线与平面,平面与平面之间没有公共点就平行,平行就没有公共点,这句话对吗?为什么?3.直线与直线,直线与平面,平面与平面之间有两个公共点时,它们的位置关系如何?4.如果平面与平面有三个公共点时位置关系如何?练习巩固:1.如果三个平面两两相交,那么它们的交线有多少条?画出图形表示你的结论。答:有可能1条,也有可能3条交线。(1)(2)2.平面α//平面β,且aìα,下列四个命题:
A、a与β内的所有直线平行??????????????????
B、a与β内的无数条直线平行???????????????
C、a与β内的任一直线都不垂直?????????????
D、a与β无公共点??????????????????????????其中假命题为(????)练习巩固:例. 下列命题中正确的个数是
①若直线l上有无数个点不在平面?内,
则l∥?.
②若直线l与平面?平行,则l与平面?内
的任意一条直线都平行.
③如果两条平行直线中的一条与一个平
面平行,那么另一条也与这个平面平行.
④若直线l与平面?平行,则l与平面?内
的任意一条直线都没有公共点.A. 0 B. 1 C. 2 D. 3切割长方体一个长方体切一刀可以分成多少块?
一个长方体切两刀可以分成多少块?
一个长方体切三刀可以分成多少块?
23或44或6或7或8课堂讨论一个长方体切三刀可以分成多少块?练习巩固:(2)(3)(4)(5)466781、空间中两条直线有几种位置关系?分别是什么?(1)相交;(2)平行;(3)异面2、直线与平面有几种位置关系?分别是什么?(1)直线在平面内——有无数个公共点:?
(2)直线与平面相交——有且只有一个公共点;?
(3)直线与平面平行——没有公共点;
其中直线与平面相交或平行的情况统称为直线
在平面外.3.平面之间的关系有几种?(1)两个平面平行――没有公共点;
(2)两个平面相交――有一条公共直线。小结下课
