【双减-同步分层作业】27.2.3相似三角形应用举例(含解析)
文档属性
| 名称 | 【双减-同步分层作业】27.2.3相似三角形应用举例(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 15:01:31 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【双减—同步分层作业】27.2.3相似三角形应用举例
1、 知识梳理
1 2
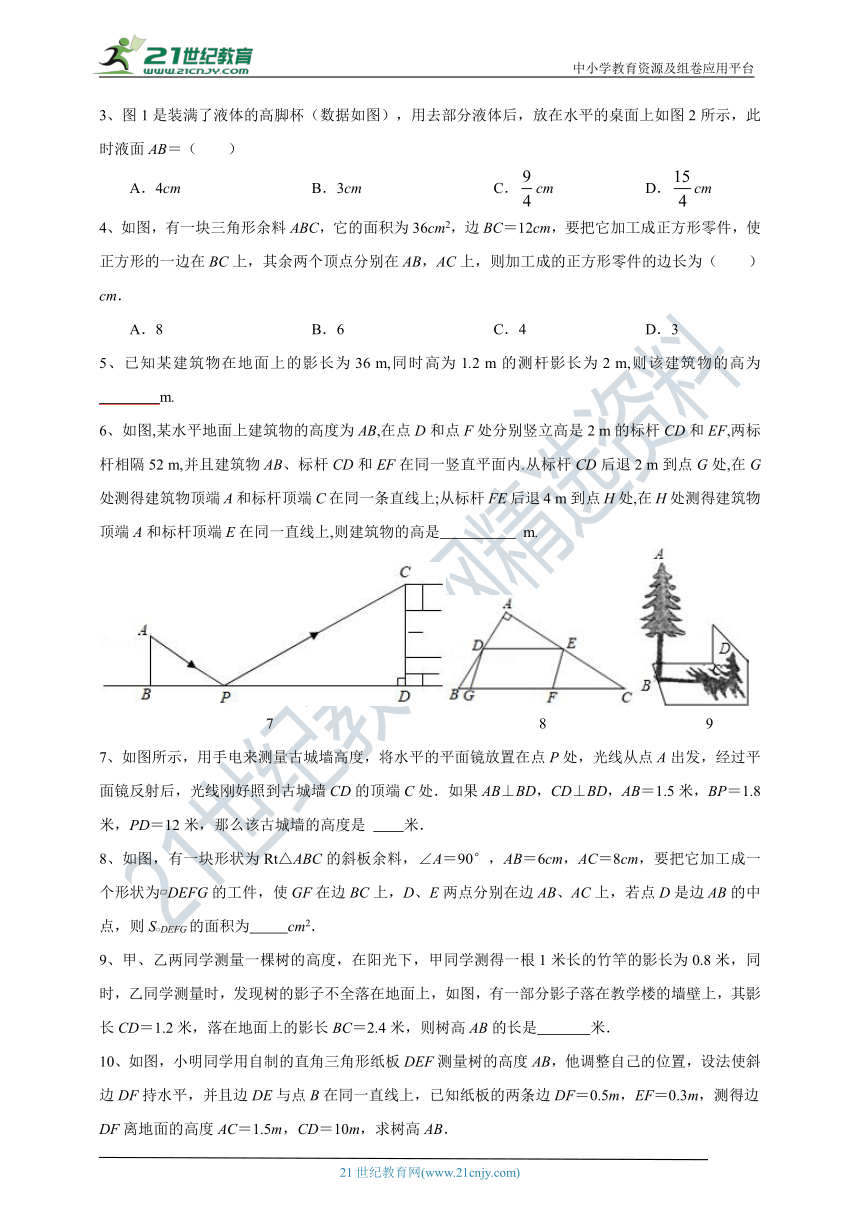
1、如图,某同学利用标杆BE测量教学楼的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则教学楼CD的高度是 m.
2、如图是小孔成像原理的示意图,点O与物体AB距离为30cm,与像CD的距离是14cm,AB∥CD.若物体AB的高度为15cm,则像CD的高度是 cm.
二、夯实基础(必做题)
1 2
1、如图,小明在打网球时,要使球恰好能过网,而且落在离网5 m的位置上,则球拍击球的高度h应为( )
A.1.8 m B.2.7 m C.3.6 m D.4.5 m
2、据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD.若物体AB的高为6cm,小孔O到物体和实像的水平距离BE,CE分别为8cm,6cm,则实像CD的高度为( )
A.4cm B.4.5cm C.5cm D.6cm
3 4 6
3、图1是装满了液体的高脚杯(数据如图),用去部分液体后,放在水平的桌面上如图2所示,此时液面AB=( )
A.4cm B.3cm C.cm D.cm
4、如图,有一块三角形余料ABC,它的面积为36cm2,边BC=12cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则加工成的正方形零件的边长为( )cm.
A.8 B.6 C.4 D.3
5、已知某建筑物在地面上的影长为36 m,同时高为1.2 m的测杆影长为2 m,则该建筑物的高为 ________m.
6、如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2 m的标杆CD和EF,两标杆相隔52 m,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2 m到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4 m到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,则建筑物的高是 m.
7 8 9
7、如图所示,用手电来测量古城墙高度,将水平的平面镜放置在点P处,光线从点A出发,经过平面镜反射后,光线刚好照到古城墙CD的顶端C处.如果AB⊥BD,CD⊥BD,AB=1.5米,BP=1.8米,PD=12米,那么该古城墙的高度是 米.
8、如图,有一块形状为Rt△ABC的斜板余料,∠A=90°,AB=6cm,AC=8cm,要把它加工成一个形状为 DEFG的工件,使GF在边BC上,D、E两点分别在边AB、AC上,若点D是边AB的中点,则S DEFG的面积为 cm2.
9、甲、乙两同学测量一棵树的高度,在阳光下,甲同学测得一根1米长的竹竿的影长为0.8米,同时,乙同学测量时,发现树的影子不全落在地面上,如图,有一部分影子落在教学楼的墙壁上,其影长CD=1.2米,落在地面上的影长BC=2.4米,则树高AB的长是 米.
10、如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF持水平,并且边DE与点B在同一直线上,已知纸板的两条边DF=0.5m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
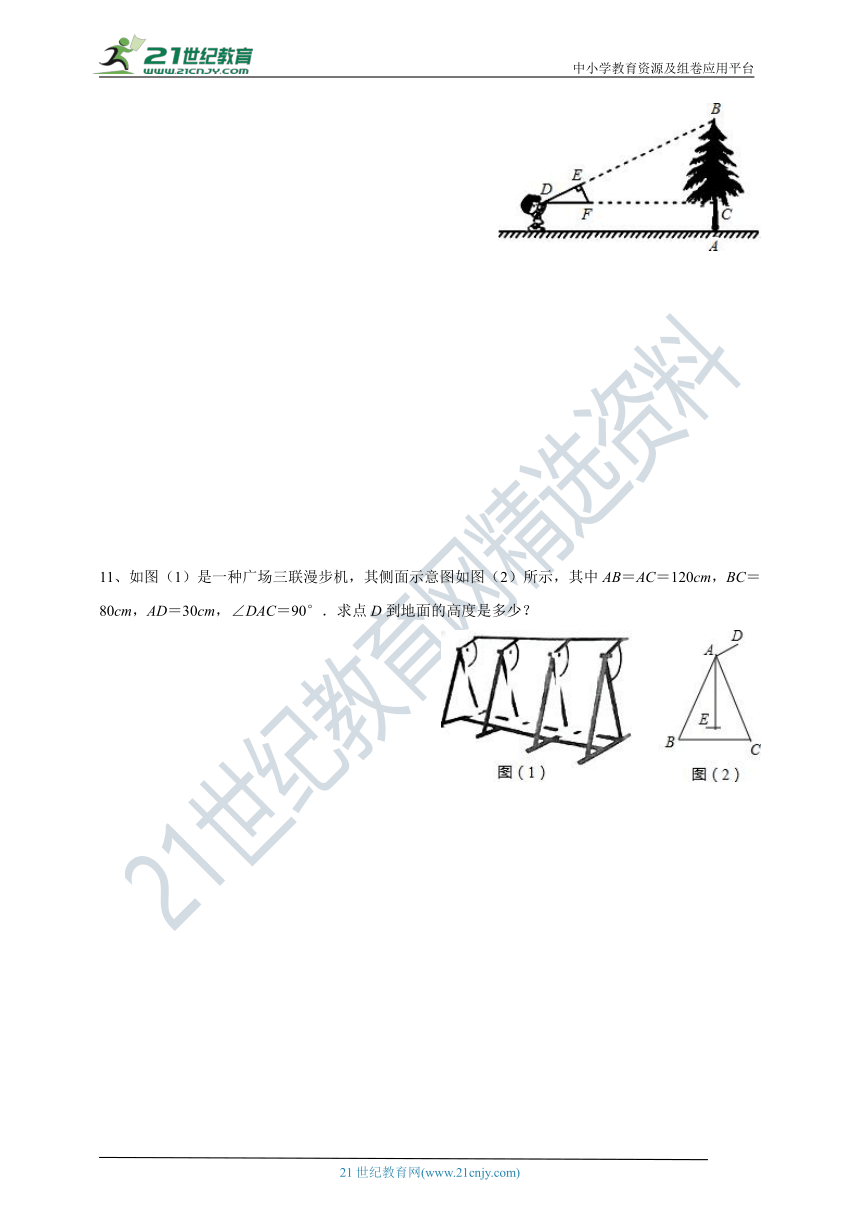
11、如图(1)是一种广场三联漫步机,其侧面示意图如图(2)所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°.求点D到地面的高度是多少?
12、某市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位,公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点B,C在EF上,EF∥HG,EH⊥HG.已知AB=80cm,AD=24cm,BC=25cm,EH=4cm,求点A到地面的距离.
13、如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使一边在BC上,其余两个顶点分别在边AB、AC上.
(1)求证:△APQ∽△ABC;
(2)若这个矩形的边PN:PQ=2:1,则这个矩形的长、宽各是多少?
三、能力提升(中等生加练题)
1、西安市的大雁塔又名“慈恩寺塔”,是国家级文物保护单位,玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔,最初五层,后加盖至九层,是西安市的标志性建筑之一,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米,请你根据以上数据,计算大雁塔的高度AB.
2、李师傅用镜子测量一棵古树的高,但树旁有一条小河,不便测量镜子与树之间的距离,于是他两次利用镜子,第一次把镜子放在C点(如图所示),人在F点正好在镜中看到树尖A;第二次他把镜子放在C′处,人在F′处正好看到树尖A.已知李师傅眼睛距地面的高度为1.7m,量得CC′为12m,CF为1.8m,C′F′为3.84m,求树高.
四、拓展训练(尖子生加练题)
1、为更好筹备“十四运”的召开,小颖及其小组成员将利用所学知识测量一个广告牌的高度EF.在第一次测量中,小颖来回走动,走到点D时,其影子末端与广告牌影子末端重合于点H,其中DH=1m.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小颖从点D沿着直线FD后退5m到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2m.
如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小颖的身高为1.5m(眼睛到头顶距离忽略不计),平面镜的厚度忽略不计.根据以上信息,求广告牌的高度EF.
2、八(一)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后回答下列问题:
(1)方案(Ⅰ)是否可行?请说明理由;
(2)方案(Ⅱ)是否可行?请说明理由;
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)是否成立? .
【参考答案】
一、
1、17.5
2、7
二、
1、B
2、B
3、C
4、C
5、21.6
6、54
7、10
8、12 解:过点A作AM⊥BC,交DE于点N
∵∠A=90°,AB=6cm,AC=8cm,
∴
∵
∴,即
∵四边形DEFG是平行四边形
∴DE∥BC
又∵点D是边AB的中点
∴DE=BC=5cm
∴DE=FG=5cm
∴△ADE∽△ABC
∴
∴AN=MN=2.4cm
∴ DEFG的面积为:5×2.4=12(cm2)
9、4.2 解:设从墙上的影子的顶端到树的顶端的垂直高度是x米.
则有
解得x=3
树高是3+1.2=4.2米
10、解:∵∠DEF=∠DCB=90°,∠EDF=∠CDB
∴△DEF∽△DCB
∴
在Rt△DEF中
∵DF=0.5m,EF=0.3m
由勾股定理得
∵CD=10m
∴
∴BC=7.5m
∴AB=AC+BC=1.5+7.5=9m
答:树高AB是9m。
11、解:过A作AF⊥BC,垂足为F,过点D作DH⊥AF,垂足为H.
∵AF⊥BC,垂足为F,
∴BF=FC=BC=40cm
根据勾股定理,得
∵∠DHA=∠DAC=∠AFC=90°
∴∠DAH+∠FAC=90°,∠C+∠FAC=90°
∴∠DAH=∠C,
∴△DAH∽△ACF,
∴
∴
∴AH=10cm
∴HF=(10+80)cm
答:D到地面的高度为(10+80)cm。
12、解:过点A作AM⊥BF于点M,过点C作CN⊥AB于点N,
∵AD=24cm,则NC=24cm,
∴
∵∠AMB=∠CNB=90°,∠ABM=∠CBN
∴△BNC∽△BMA
∴
即
则
∴点A到地面的距离是
答:点A到地面的距离是cm。
13、解:(1)∵四边形PNQM为矩形
∴MN∥PQ
即PQ∥BC
∴△APQ∽△ABC
(2)设边宽为xmm,则长为2xmm
∵四边形PNMQ为矩形
∴PQ∥BC
∵AD⊥BC
∴PQ⊥AD
∵PN:PQ=2:1
∴PQ为长,PN为宽
∵PQ∥BC
∴△APQ∽△ABC
∴
由题意知PQ=2xmm,AD=80mm,BC=120mm,PN=xmm
∴
解得x=,2x=.
即长为mm,宽为mm.
答:矩形的长mm,宽为mm。
三、
1、解:∵△EDC∽△EBA,△FHG∽△FBA,
∴
∵DC=HG
∴
即
∴CA=106米
∵
∴
∴AB=55米
答:大雁塔的高度AB为55米。
2、解:根据反射定律可以推出∠ACB=∠ECF,∠AC′B=∠E′C′F′
∴△BAC∽△FEC、△AC′B∽△E′C′F′
设AB=x,BC=y
∴
解得
答:这棵古树的高为10m。
四、
1、解:设广告牌的高度EF为xm,
依题意知:DB=5m,BG=2m,DH=1m,AB=CD=1.5m
∴GD=DB﹣BG=3m,
∵CD⊥BF,EF⊥BF,
∴CD∥EF.
∴△EFH∽△CDH.
∴,即
∴
∴
由平面镜反射规律可得:∠EGF=∠AGB
∵AB⊥BF,
∴∠ABG=90°=∠EFG.
∴△EFG∽△ABG.
∴,即
∴
∴x=3
答:广告牌的高度EF为3m。
2、解:(1)方案(Ⅰ)可行;
∵DC=AC,EC=BC且有对顶角∠ACB=∠DCE
∴△ACB≌△DCE(SAS)
∴AB=DE
∴测出DE的距离即为AB的长
故方案(Ⅰ)可行。
(2)方案(Ⅱ)可行;
∵AB⊥BC,DE⊥CD
∴∠ABC=∠EDC=90°
又∵BC=CD,∠ACB=∠ECD
∴△ABC≌△EDC
∴AB=ED
∴测出DE的长即为AB的距离
故方案(Ⅱ)可行。
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是∠ABD=∠BDE.
若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)不成立;
理由:若∠ABD=∠BDE≠90°,∠ACB=∠ECD,
∴△ABC∽△EDC,
∴
∴只要测出ED、BC、CD的长,即可求得AB的长
但是此题没有其他条件,可能无法测出其他线段长度
∴方案(Ⅱ)不成立。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【双减—同步分层作业】27.2.3相似三角形应用举例
1、 知识梳理
1 2
1、如图,某同学利用标杆BE测量教学楼的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则教学楼CD的高度是 m.
2、如图是小孔成像原理的示意图,点O与物体AB距离为30cm,与像CD的距离是14cm,AB∥CD.若物体AB的高度为15cm,则像CD的高度是 cm.
二、夯实基础(必做题)
1 2
1、如图,小明在打网球时,要使球恰好能过网,而且落在离网5 m的位置上,则球拍击球的高度h应为( )
A.1.8 m B.2.7 m C.3.6 m D.4.5 m
2、据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD.若物体AB的高为6cm,小孔O到物体和实像的水平距离BE,CE分别为8cm,6cm,则实像CD的高度为( )
A.4cm B.4.5cm C.5cm D.6cm
3 4 6
3、图1是装满了液体的高脚杯(数据如图),用去部分液体后,放在水平的桌面上如图2所示,此时液面AB=( )
A.4cm B.3cm C.cm D.cm
4、如图,有一块三角形余料ABC,它的面积为36cm2,边BC=12cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则加工成的正方形零件的边长为( )cm.
A.8 B.6 C.4 D.3
5、已知某建筑物在地面上的影长为36 m,同时高为1.2 m的测杆影长为2 m,则该建筑物的高为 ________m.
6、如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2 m的标杆CD和EF,两标杆相隔52 m,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2 m到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4 m到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,则建筑物的高是 m.
7 8 9
7、如图所示,用手电来测量古城墙高度,将水平的平面镜放置在点P处,光线从点A出发,经过平面镜反射后,光线刚好照到古城墙CD的顶端C处.如果AB⊥BD,CD⊥BD,AB=1.5米,BP=1.8米,PD=12米,那么该古城墙的高度是 米.
8、如图,有一块形状为Rt△ABC的斜板余料,∠A=90°,AB=6cm,AC=8cm,要把它加工成一个形状为 DEFG的工件,使GF在边BC上,D、E两点分别在边AB、AC上,若点D是边AB的中点,则S DEFG的面积为 cm2.
9、甲、乙两同学测量一棵树的高度,在阳光下,甲同学测得一根1米长的竹竿的影长为0.8米,同时,乙同学测量时,发现树的影子不全落在地面上,如图,有一部分影子落在教学楼的墙壁上,其影长CD=1.2米,落在地面上的影长BC=2.4米,则树高AB的长是 米.
10、如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF持水平,并且边DE与点B在同一直线上,已知纸板的两条边DF=0.5m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
11、如图(1)是一种广场三联漫步机,其侧面示意图如图(2)所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°.求点D到地面的高度是多少?
12、某市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位,公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点B,C在EF上,EF∥HG,EH⊥HG.已知AB=80cm,AD=24cm,BC=25cm,EH=4cm,求点A到地面的距离.
13、如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使一边在BC上,其余两个顶点分别在边AB、AC上.
(1)求证:△APQ∽△ABC;
(2)若这个矩形的边PN:PQ=2:1,则这个矩形的长、宽各是多少?
三、能力提升(中等生加练题)
1、西安市的大雁塔又名“慈恩寺塔”,是国家级文物保护单位,玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔,最初五层,后加盖至九层,是西安市的标志性建筑之一,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米,请你根据以上数据,计算大雁塔的高度AB.
2、李师傅用镜子测量一棵古树的高,但树旁有一条小河,不便测量镜子与树之间的距离,于是他两次利用镜子,第一次把镜子放在C点(如图所示),人在F点正好在镜中看到树尖A;第二次他把镜子放在C′处,人在F′处正好看到树尖A.已知李师傅眼睛距地面的高度为1.7m,量得CC′为12m,CF为1.8m,C′F′为3.84m,求树高.
四、拓展训练(尖子生加练题)
1、为更好筹备“十四运”的召开,小颖及其小组成员将利用所学知识测量一个广告牌的高度EF.在第一次测量中,小颖来回走动,走到点D时,其影子末端与广告牌影子末端重合于点H,其中DH=1m.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小颖从点D沿着直线FD后退5m到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2m.
如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小颖的身高为1.5m(眼睛到头顶距离忽略不计),平面镜的厚度忽略不计.根据以上信息,求广告牌的高度EF.
2、八(一)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后回答下列问题:
(1)方案(Ⅰ)是否可行?请说明理由;
(2)方案(Ⅱ)是否可行?请说明理由;
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)是否成立? .
【参考答案】
一、
1、17.5
2、7
二、
1、B
2、B
3、C
4、C
5、21.6
6、54
7、10
8、12 解:过点A作AM⊥BC,交DE于点N
∵∠A=90°,AB=6cm,AC=8cm,
∴
∵
∴,即
∵四边形DEFG是平行四边形
∴DE∥BC
又∵点D是边AB的中点
∴DE=BC=5cm
∴DE=FG=5cm
∴△ADE∽△ABC
∴
∴AN=MN=2.4cm
∴ DEFG的面积为:5×2.4=12(cm2)
9、4.2 解:设从墙上的影子的顶端到树的顶端的垂直高度是x米.
则有
解得x=3
树高是3+1.2=4.2米
10、解:∵∠DEF=∠DCB=90°,∠EDF=∠CDB
∴△DEF∽△DCB
∴
在Rt△DEF中
∵DF=0.5m,EF=0.3m
由勾股定理得
∵CD=10m
∴
∴BC=7.5m
∴AB=AC+BC=1.5+7.5=9m
答:树高AB是9m。
11、解:过A作AF⊥BC,垂足为F,过点D作DH⊥AF,垂足为H.
∵AF⊥BC,垂足为F,
∴BF=FC=BC=40cm
根据勾股定理,得
∵∠DHA=∠DAC=∠AFC=90°
∴∠DAH+∠FAC=90°,∠C+∠FAC=90°
∴∠DAH=∠C,
∴△DAH∽△ACF,
∴
∴
∴AH=10cm
∴HF=(10+80)cm
答:D到地面的高度为(10+80)cm。
12、解:过点A作AM⊥BF于点M,过点C作CN⊥AB于点N,
∵AD=24cm,则NC=24cm,
∴
∵∠AMB=∠CNB=90°,∠ABM=∠CBN
∴△BNC∽△BMA
∴
即
则
∴点A到地面的距离是
答:点A到地面的距离是cm。
13、解:(1)∵四边形PNQM为矩形
∴MN∥PQ
即PQ∥BC
∴△APQ∽△ABC
(2)设边宽为xmm,则长为2xmm
∵四边形PNMQ为矩形
∴PQ∥BC
∵AD⊥BC
∴PQ⊥AD
∵PN:PQ=2:1
∴PQ为长,PN为宽
∵PQ∥BC
∴△APQ∽△ABC
∴
由题意知PQ=2xmm,AD=80mm,BC=120mm,PN=xmm
∴
解得x=,2x=.
即长为mm,宽为mm.
答:矩形的长mm,宽为mm。
三、
1、解:∵△EDC∽△EBA,△FHG∽△FBA,
∴
∵DC=HG
∴
即
∴CA=106米
∵
∴
∴AB=55米
答:大雁塔的高度AB为55米。
2、解:根据反射定律可以推出∠ACB=∠ECF,∠AC′B=∠E′C′F′
∴△BAC∽△FEC、△AC′B∽△E′C′F′
设AB=x,BC=y
∴
解得
答:这棵古树的高为10m。
四、
1、解:设广告牌的高度EF为xm,
依题意知:DB=5m,BG=2m,DH=1m,AB=CD=1.5m
∴GD=DB﹣BG=3m,
∵CD⊥BF,EF⊥BF,
∴CD∥EF.
∴△EFH∽△CDH.
∴,即
∴
∴
由平面镜反射规律可得:∠EGF=∠AGB
∵AB⊥BF,
∴∠ABG=90°=∠EFG.
∴△EFG∽△ABG.
∴,即
∴
∴x=3
答:广告牌的高度EF为3m。
2、解:(1)方案(Ⅰ)可行;
∵DC=AC,EC=BC且有对顶角∠ACB=∠DCE
∴△ACB≌△DCE(SAS)
∴AB=DE
∴测出DE的距离即为AB的长
故方案(Ⅰ)可行。
(2)方案(Ⅱ)可行;
∵AB⊥BC,DE⊥CD
∴∠ABC=∠EDC=90°
又∵BC=CD,∠ACB=∠ECD
∴△ABC≌△EDC
∴AB=ED
∴测出DE的长即为AB的距离
故方案(Ⅱ)可行。
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是∠ABD=∠BDE.
若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)不成立;
理由:若∠ABD=∠BDE≠90°,∠ACB=∠ECD,
∴△ABC∽△EDC,
∴
∴只要测出ED、BC、CD的长,即可求得AB的长
但是此题没有其他条件,可能无法测出其他线段长度
∴方案(Ⅱ)不成立。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
