【双减-同步分层作业】27.3位似(含解析)
文档属性
| 名称 | 【双减-同步分层作业】27.3位似(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【双减—同步分层作业】27.3位似
一、知识梳理
1 2
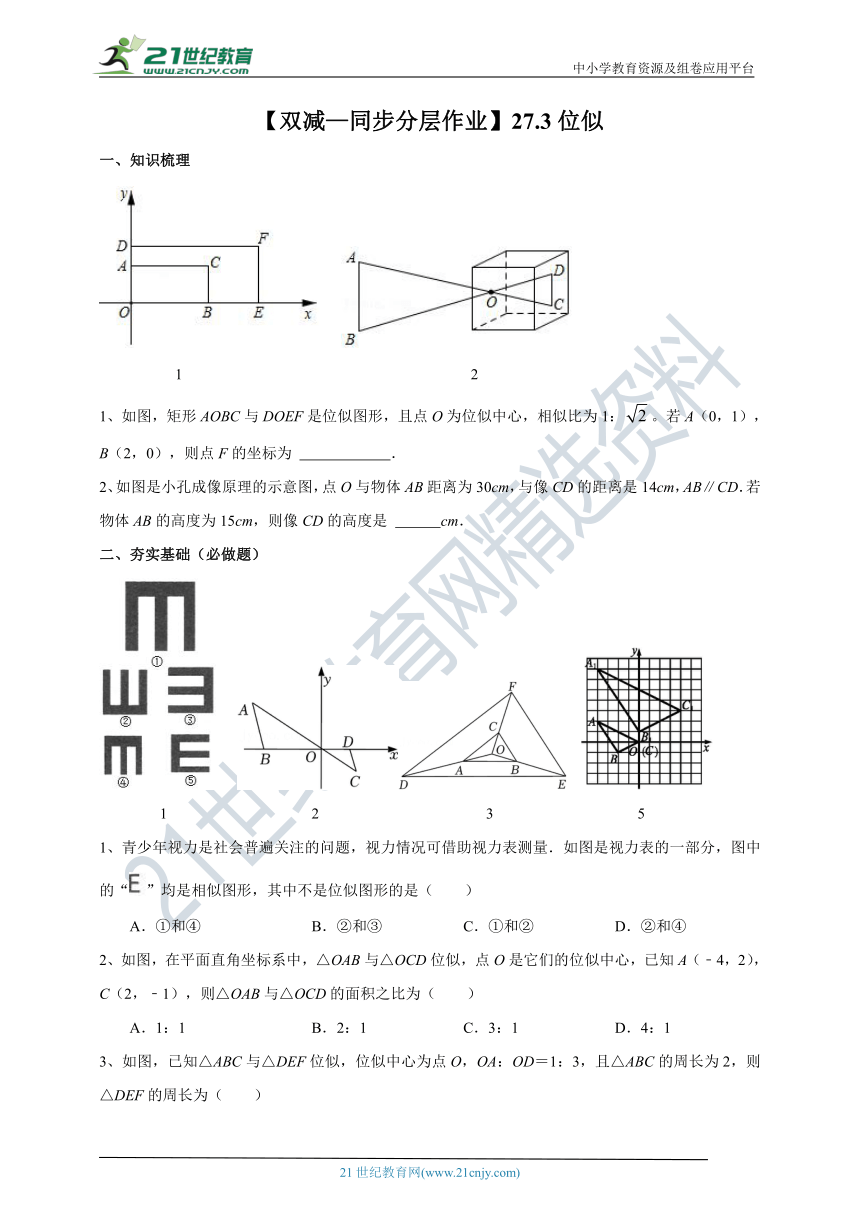
1、如图,矩形AOBC与DOEF是位似图形,且点O为位似中心,相似比为1:。若A(0,1),B(2,0),则点F的坐标为 .
2、如图是小孔成像原理的示意图,点O与物体AB距离为30cm,与像CD的距离是14cm,AB∥CD.若物体AB的高度为15cm,则像CD的高度是 cm.
二、夯实基础(必做题)
1 2 3 5
1、青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.如图是视力表的一部分,图中的“”均是相似图形,其中不是位似图形的是( )
A.①和④ B.②和③ C.①和② D.②和④
2、如图,在平面直角坐标系中,△OAB与△OCD位似,点O是它们的位似中心,已知A(﹣4,2),C(2,﹣1),则△OAB与△OCD的面积之比为( )
A.1:1 B.2:1 C.3:1 D.4:1
3、如图,已知△ABC与△DEF位似,位似中心为点O,OA:OD=1:3,且△ABC的周长为2,则△DEF的周长为( )
A.4 B.6 C.8 D.18
4、在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E'的坐标是( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
5、如图,将△ABC的三边分别放大为原来的2倍得到△A1B1C1(顶点均在格点上),它们是以点P为位似中心的位似图形,则点P的坐标是( )
A.(-4,-3) B.(-3,-3) C.(-4,-4) D.(-3,-4)
6、已知点A、B的坐标分别为A(﹣4,2)、B(﹣1,﹣1),以原点O为位似中心,按相似比
1:2把△ABO缩小,则点A的对应点A'的坐标为 .
7、下列关于位似图形的表述正确的是 .(只填序号)
①相似图形一定是位似图形,位似图形一定是相似图形
②位似图形一定有位似中心
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形
④位似图形上任意两点与位似中心的距离之比等于相似比
8、如图,原点O是△ABC和△A'B'C'的位似中心,点A(1,0)与A'(-2,0)是对应点,△ABC的面积是,则△A'B'C'的面积是
9、如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且,则=
10、如图,A是反比例函数(x>0)图象上的一点,点B、D在y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3,△ABD的面积为1,则k的值为 .
11、如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
(1)请你根据位似的特征并结合点B的坐标变化回答下列问题:
①若点A(,3),则A′的坐标为 ;
②△ABC与△A′B′C′的相似比为 ;
(2)若△ABC的面积为m,求△A′B′C′的面积.(用含m的代数式表示)
12、如图,梯形ABCD的四个顶点分别为A(0,6),B(2,2),C(4,2),D(6,6)。按下列要求画图。
(1)在平面直角坐标系中,画出以原点O为位似中心,相似比为的位似图形A1B1C1D1;
(2)画出位似图形A1B1C1D1向下平移5个单位长度后的图形A2B2C2D2。
13、已知平面直角坐标系如图所示。
(1)描出下列各点:A(1,0),B(3,0),C(3,3),D(0,1),并将这些点用线段依次连接起来;
(2)以坐标原点O为位似中心,把(1)中所得图形放大为原来的2倍。
三、能力提升(中等生加练题)
1、如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1。
(1)求△A1B1C1与△ABC的相似比;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)设点P(a,b)为△ABC内一点,求依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标。
2、如图所示,在平面直角坐标系中有一格点三角形,该三角形的三个顶点为:A(1,1),
B(﹣3,1),C(﹣3,﹣1).
(1)若△ABC的外接圆的圆心为P,则点P的坐标为 ,⊙P的半径为 ;
(2)如图所示,在11×8的网格图内,以坐标原点O点为位似中心,将△ABC按相似比2:1放大,A、B、C的对应点分别为A'、B'、C'.①画出△A'B'C';②将△A'B'C'沿x轴方向平移,需平移 个单位长度,能使得B'C'所在的直线与⊙P相切。
四、拓展训练(尖子生加练题)
1、如图,△ABC中,P′是边AB上一点,四边形P'Q'M'N'是正方形,点Q',M'在边BC上,点N′在△ABC内.连接BN′,并延长交AC于点N,过点N作NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
(1)求证:四边形PQMN为正方形;
(2)若∠A=90°,AC=1.5m,△ABC的面积=1.5m2.求PN的长.
2、已知:如图,△ABC是⊙O的内接正三角形,点D是的中点,连接BD并延长BD到点E,使BD=DE,连接CD和DE.
(1)求证:△CDE是正三角形.
(2)问:△CDE经怎样的变换后能与△ABC成位似图形?请在图中直接画出△CDE变换后的对应三角形△CD'E',并求出△CD'E'与△ABC的位似比.
【参考答案】
一、
1、
2、7
二、
1、B
2、D
3、B
4、D
5、A 因为是放大为原来的2倍,且点A1、A同在一条纵线上,所以点P一定也在A1A的延长线上,设AP=x,所以有,解得x=5,所以点P的坐标是(-4,-3)。
6、(-2,1)或(2,-1)
7、②③
8、6 由题意得,相似比为2,所以S△ABC∶S△A'B'C'=1∶4,
即∶S△A'B'C'=1∶4,所以S△A'B'C'=6
9、
10、8
解:过A作AE⊥x轴,
∵△ABD是△COD关于点D的位似图形,
且△ABD与△COD的位似是1:3
∴
∴OE=AB
∴
假设BD=x,AB=y
∴DO=3x,AE=4x,CO=3y,
∵△ABD的面积为1,
∴xy=1
∴xy=2
∴AB AE=4xy=8
即k=4xy=8
(1)①(5,6)
②1:2
(2)解:∵△ABC与△A'B'C'的相似比为1:2
∴
而△ABC的面积为m
∴△A′B′C′的面积=4m
12、解:(1)图形A1B1C1D1如图所示;
(2)图形A2B2C2D2如图所示。
13、解:如图:
(1)顺次连接点A,B,C,,D得四边形ABCD;
(2)以点O为位似中心,把四边形ABCD放大为原来的2倍,得新四边形A1B1C1D1和四边形A2B2C2D2。
三、
1、解:(1)△A1B1C1与△ABC的相似比等于
(2)如图所示。
(3)点P(a,b)为△ABC内一点,依次经过题中的两次变换后,点P的对应点P2的坐标为(-2a,2b)。
2、解:(1)△ABC的外接圆⊙P如图所示
由图可知,点P的坐标为(﹣1,0),半径为
(2)如图所示,△A′B′C′即为所求。
将△A′B′C′向右平移或个单位B′C′所在的直线与⊙P相切,
故答案为:或。
四、
1、(1)证明:∵NM⊥BC,NP⊥MN,PQ⊥BC,
∴四边形PQMN为矩形,
∵四边形P'Q'M'N'是正方形,
∴PN∥P′N′,
∴
∵MN∥M′N′
∴
∴
而
∴PN=MN
∴四边形PQMN为正方形。
(2)解:作AD⊥BC于D,AD交PN于E,如图
∵△ABC的面积=1.5
∴AB AC=1.5
∴AB=2
∴.
∵BC AD=1.5,
∴
设PN=x,则PQ=DE=x,AE=
∵PN∥BC,
∴△APN∽△ABC,
∴,即,解得x=
∴PN的长为m。
2、解:(1)证明:∵△ABC是⊙O的内接正三角形,
∴∠BAC=60°,
∴∠CDE=60°,
∵点D是的中点,
∴BD=CD,
∵BD=DE,
∴CD=DE,
∴△CDE是正三角形。
(2)如图:当△CDE绕点C旋转∠ACD的度数时与△ABC成位似图形
∵∠BDC=120°,BD=CD,
∴∠CBD=∠BCD=30°,
∵∠ACB=60°,
∴∠ACD=90°,
∴当△CDE绕点C旋转90°时与△ABC成位似图形,
作DF⊥BC于F点,
设DC=2x,
∵∠BCD=30°,
∴FC=
∴BC=2FC=
∴位似比
∴位似比为。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【双减—同步分层作业】27.3位似
一、知识梳理
1 2
1、如图,矩形AOBC与DOEF是位似图形,且点O为位似中心,相似比为1:。若A(0,1),B(2,0),则点F的坐标为 .
2、如图是小孔成像原理的示意图,点O与物体AB距离为30cm,与像CD的距离是14cm,AB∥CD.若物体AB的高度为15cm,则像CD的高度是 cm.
二、夯实基础(必做题)
1 2 3 5
1、青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.如图是视力表的一部分,图中的“”均是相似图形,其中不是位似图形的是( )
A.①和④ B.②和③ C.①和② D.②和④
2、如图,在平面直角坐标系中,△OAB与△OCD位似,点O是它们的位似中心,已知A(﹣4,2),C(2,﹣1),则△OAB与△OCD的面积之比为( )
A.1:1 B.2:1 C.3:1 D.4:1
3、如图,已知△ABC与△DEF位似,位似中心为点O,OA:OD=1:3,且△ABC的周长为2,则△DEF的周长为( )
A.4 B.6 C.8 D.18
4、在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E'的坐标是( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
5、如图,将△ABC的三边分别放大为原来的2倍得到△A1B1C1(顶点均在格点上),它们是以点P为位似中心的位似图形,则点P的坐标是( )
A.(-4,-3) B.(-3,-3) C.(-4,-4) D.(-3,-4)
6、已知点A、B的坐标分别为A(﹣4,2)、B(﹣1,﹣1),以原点O为位似中心,按相似比
1:2把△ABO缩小,则点A的对应点A'的坐标为 .
7、下列关于位似图形的表述正确的是 .(只填序号)
①相似图形一定是位似图形,位似图形一定是相似图形
②位似图形一定有位似中心
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形
④位似图形上任意两点与位似中心的距离之比等于相似比
8、如图,原点O是△ABC和△A'B'C'的位似中心,点A(1,0)与A'(-2,0)是对应点,△ABC的面积是,则△A'B'C'的面积是
9、如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且,则=
10、如图,A是反比例函数(x>0)图象上的一点,点B、D在y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3,△ABD的面积为1,则k的值为 .
11、如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
(1)请你根据位似的特征并结合点B的坐标变化回答下列问题:
①若点A(,3),则A′的坐标为 ;
②△ABC与△A′B′C′的相似比为 ;
(2)若△ABC的面积为m,求△A′B′C′的面积.(用含m的代数式表示)
12、如图,梯形ABCD的四个顶点分别为A(0,6),B(2,2),C(4,2),D(6,6)。按下列要求画图。
(1)在平面直角坐标系中,画出以原点O为位似中心,相似比为的位似图形A1B1C1D1;
(2)画出位似图形A1B1C1D1向下平移5个单位长度后的图形A2B2C2D2。
13、已知平面直角坐标系如图所示。
(1)描出下列各点:A(1,0),B(3,0),C(3,3),D(0,1),并将这些点用线段依次连接起来;
(2)以坐标原点O为位似中心,把(1)中所得图形放大为原来的2倍。
三、能力提升(中等生加练题)
1、如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1。
(1)求△A1B1C1与△ABC的相似比;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)设点P(a,b)为△ABC内一点,求依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标。
2、如图所示,在平面直角坐标系中有一格点三角形,该三角形的三个顶点为:A(1,1),
B(﹣3,1),C(﹣3,﹣1).
(1)若△ABC的外接圆的圆心为P,则点P的坐标为 ,⊙P的半径为 ;
(2)如图所示,在11×8的网格图内,以坐标原点O点为位似中心,将△ABC按相似比2:1放大,A、B、C的对应点分别为A'、B'、C'.①画出△A'B'C';②将△A'B'C'沿x轴方向平移,需平移 个单位长度,能使得B'C'所在的直线与⊙P相切。
四、拓展训练(尖子生加练题)
1、如图,△ABC中,P′是边AB上一点,四边形P'Q'M'N'是正方形,点Q',M'在边BC上,点N′在△ABC内.连接BN′,并延长交AC于点N,过点N作NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
(1)求证:四边形PQMN为正方形;
(2)若∠A=90°,AC=1.5m,△ABC的面积=1.5m2.求PN的长.
2、已知:如图,△ABC是⊙O的内接正三角形,点D是的中点,连接BD并延长BD到点E,使BD=DE,连接CD和DE.
(1)求证:△CDE是正三角形.
(2)问:△CDE经怎样的变换后能与△ABC成位似图形?请在图中直接画出△CDE变换后的对应三角形△CD'E',并求出△CD'E'与△ABC的位似比.
【参考答案】
一、
1、
2、7
二、
1、B
2、D
3、B
4、D
5、A 因为是放大为原来的2倍,且点A1、A同在一条纵线上,所以点P一定也在A1A的延长线上,设AP=x,所以有,解得x=5,所以点P的坐标是(-4,-3)。
6、(-2,1)或(2,-1)
7、②③
8、6 由题意得,相似比为2,所以S△ABC∶S△A'B'C'=1∶4,
即∶S△A'B'C'=1∶4,所以S△A'B'C'=6
9、
10、8
解:过A作AE⊥x轴,
∵△ABD是△COD关于点D的位似图形,
且△ABD与△COD的位似是1:3
∴
∴OE=AB
∴
假设BD=x,AB=y
∴DO=3x,AE=4x,CO=3y,
∵△ABD的面积为1,
∴xy=1
∴xy=2
∴AB AE=4xy=8
即k=4xy=8
(1)①(5,6)
②1:2
(2)解:∵△ABC与△A'B'C'的相似比为1:2
∴
而△ABC的面积为m
∴△A′B′C′的面积=4m
12、解:(1)图形A1B1C1D1如图所示;
(2)图形A2B2C2D2如图所示。
13、解:如图:
(1)顺次连接点A,B,C,,D得四边形ABCD;
(2)以点O为位似中心,把四边形ABCD放大为原来的2倍,得新四边形A1B1C1D1和四边形A2B2C2D2。
三、
1、解:(1)△A1B1C1与△ABC的相似比等于
(2)如图所示。
(3)点P(a,b)为△ABC内一点,依次经过题中的两次变换后,点P的对应点P2的坐标为(-2a,2b)。
2、解:(1)△ABC的外接圆⊙P如图所示
由图可知,点P的坐标为(﹣1,0),半径为
(2)如图所示,△A′B′C′即为所求。
将△A′B′C′向右平移或个单位B′C′所在的直线与⊙P相切,
故答案为:或。
四、
1、(1)证明:∵NM⊥BC,NP⊥MN,PQ⊥BC,
∴四边形PQMN为矩形,
∵四边形P'Q'M'N'是正方形,
∴PN∥P′N′,
∴
∵MN∥M′N′
∴
∴
而
∴PN=MN
∴四边形PQMN为正方形。
(2)解:作AD⊥BC于D,AD交PN于E,如图
∵△ABC的面积=1.5
∴AB AC=1.5
∴AB=2
∴.
∵BC AD=1.5,
∴
设PN=x,则PQ=DE=x,AE=
∵PN∥BC,
∴△APN∽△ABC,
∴,即,解得x=
∴PN的长为m。
2、解:(1)证明:∵△ABC是⊙O的内接正三角形,
∴∠BAC=60°,
∴∠CDE=60°,
∵点D是的中点,
∴BD=CD,
∵BD=DE,
∴CD=DE,
∴△CDE是正三角形。
(2)如图:当△CDE绕点C旋转∠ACD的度数时与△ABC成位似图形
∵∠BDC=120°,BD=CD,
∴∠CBD=∠BCD=30°,
∵∠ACB=60°,
∴∠ACD=90°,
∴当△CDE绕点C旋转90°时与△ABC成位似图形,
作DF⊥BC于F点,
设DC=2x,
∵∠BCD=30°,
∴FC=
∴BC=2FC=
∴位似比
∴位似比为。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
