【双减—同步分层作业】28.2.1解直角三角形(含解析)
文档属性
| 名称 | 【双减—同步分层作业】28.2.1解直角三角形(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【双减—同步分层作业】28.2.1解直角三角形
一、知识梳理
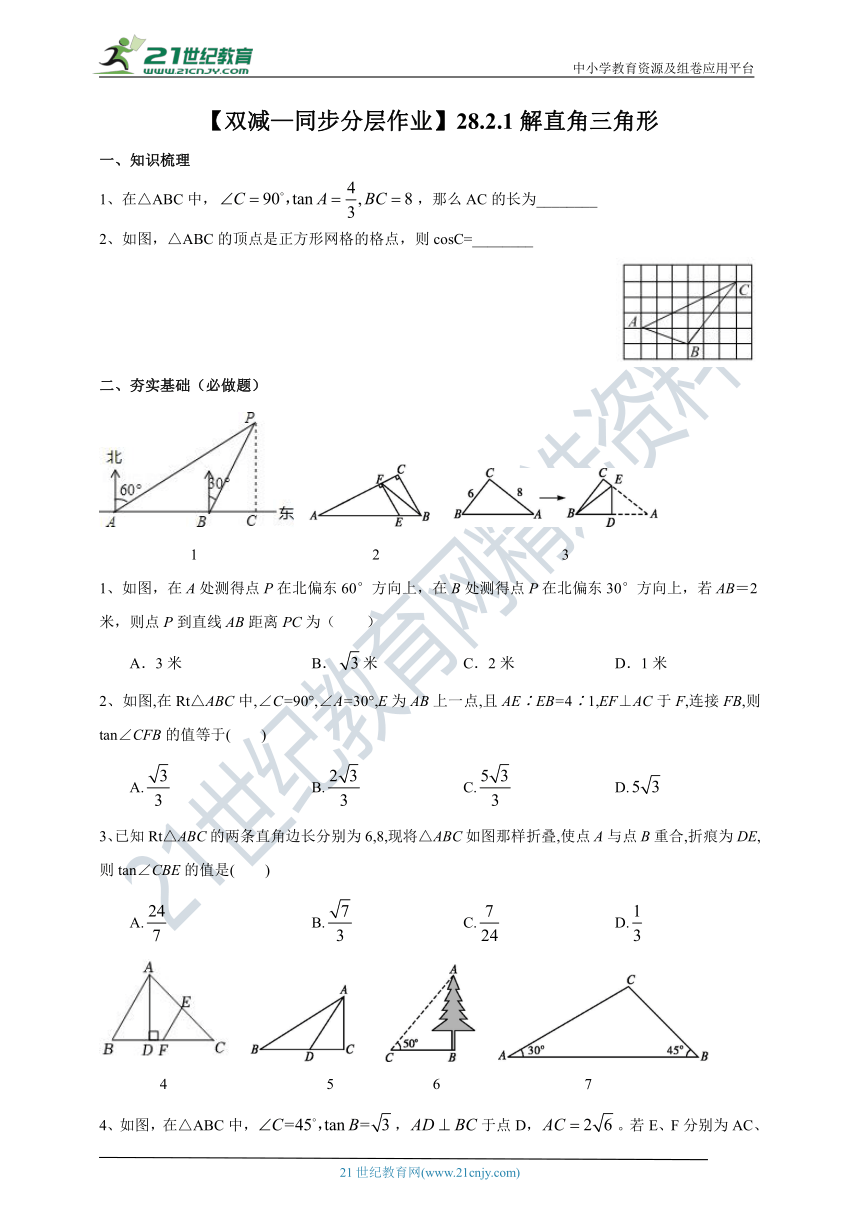
1、在△ABC中,,那么AC的长为________
2、如图,△ABC的顶点是正方形网格的格点,则cosC=________
二、夯实基础(必做题)
1 2 3
1、如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AB=2米,则点P到直线AB距离PC为( )
A.3米 B.米 C.2米 D.1米
2、如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE∶EB=4∶1,EF⊥AC于F,连接FB,则tan∠CFB的值等于( )
A. B. C. D.
3、已知Rt△ABC的两条直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
A. B. C. D.
4 5 6 7
4、如图,在△ABC中,,于点D,。若E、F分别为AC、BC的中点,则EF的长为( )
A. B.2 C. D.
5、如图,在△ABC中,∠C=90°,AC=5 cm,,∠BAC的平分线交BC于点D,AD=cm,则
BC= cm.
6、小敏想知道校园内一棵大树的高度,如图,她测得CB=10 m,∠C=50°,请你帮她算出树高AB约为
m.
7、如图,在△ABC中,∠A=30°,∠B=45°,AC=,则AB的长为 .
8、如图,在Rt△ABC中,,CD是AB边上的中线,若CD=5,BC=6,则cos=______
9、已知AD是△ABC的高,CD=1,AD=BD=,则=______
10、如图,在△ABC中,,AB=4,于点D且,求BC的长。
11、如图,△ABC中,,D是AC上一点,,,求AB的长。
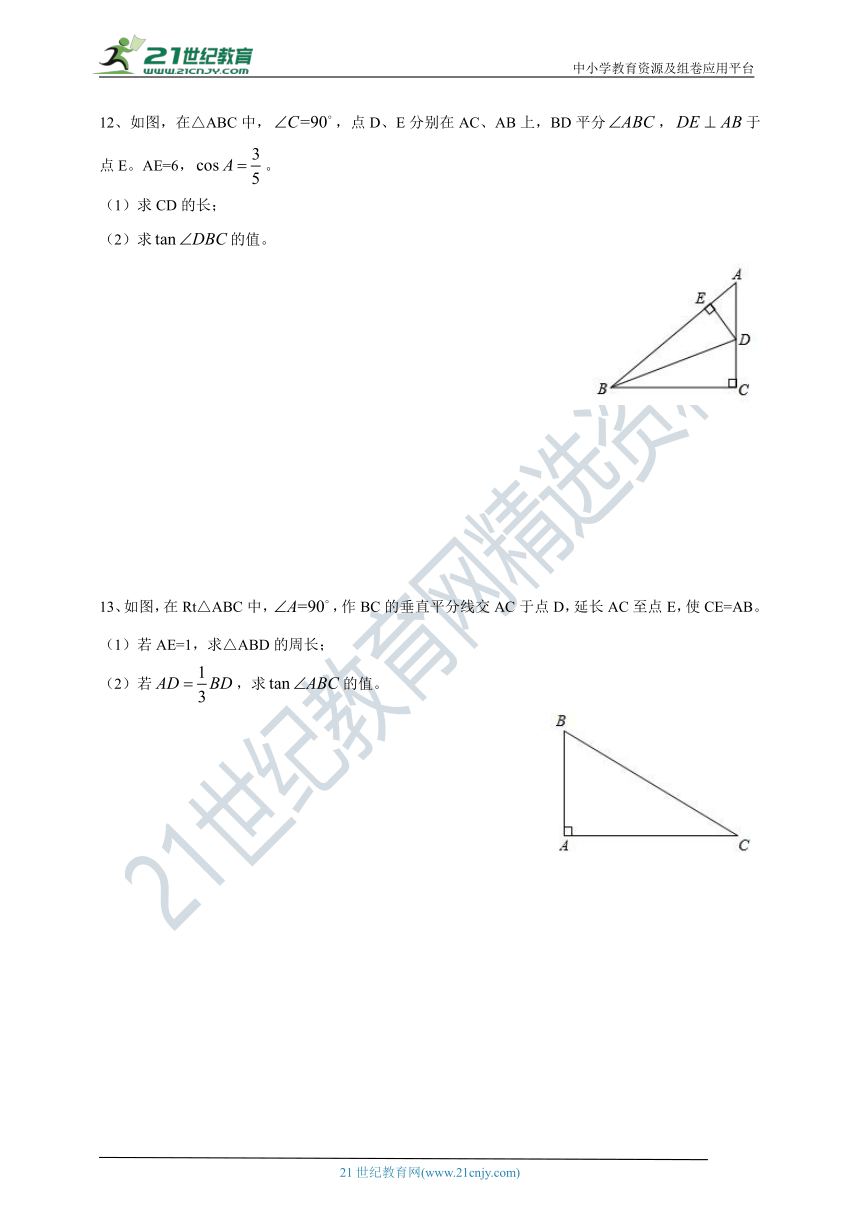
12、如图,在△ABC中,,点D、E分别在AC、AB上,BD平分,于点E。AE=6,。
(1)求CD的长;
(2)求的值。
13、如图,在Rt△ABC中,,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB。
(1)若AE=1,求△ABD的周长;
(2)若,求的值。
三、能力提升(中等生加练题)
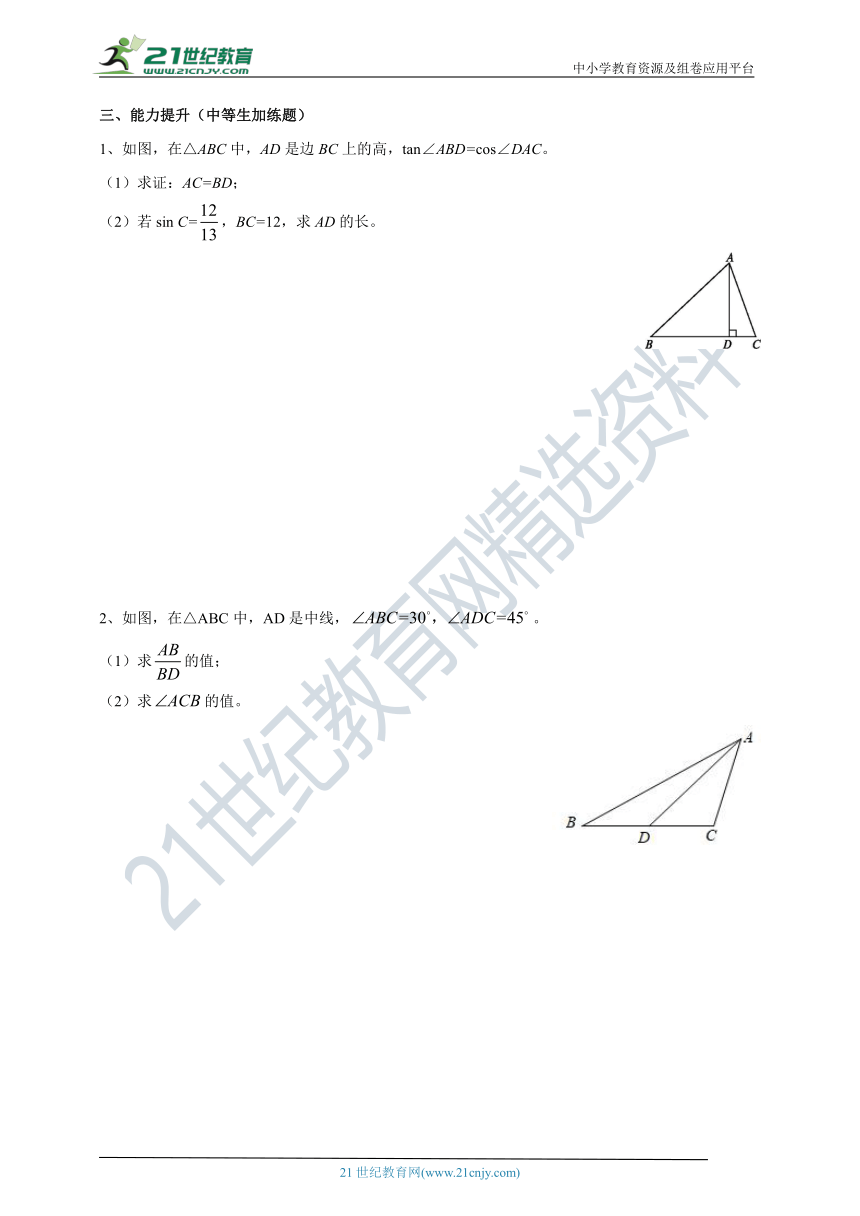
1、如图,在△ABC中,AD是边BC上的高,tan∠ABD=cos∠DAC。
(1)求证:AC=BD;
(2)若sin C=,BC=12,求AD的长。
2、如图,在△ABC中,AD是中线,。
(1)求的值;
(2)求的值。
四、拓展训练(尖子生加练题)
1、如图,已知☉O的半径为2,弦BC的长为,点A为弦BC所对优弧上任意一点(B、C两点除外)。求:
(1)∠BAC的度数;
(2)△ABC面积的最大值。
2、如图,已知BC是☉O的直径,CA平分,延长EC交☉O于点D,连接DO并延长交AB于点F。
(1)求证:;
(2)已知,求。
【参考答案】
一、
1、6
2、
二、
1、B
2、C
3、C
4、B
5、12 AB=BC·tanC=10×tan50°≈12(m)
6、26
7、 如图,过点C作CD⊥AB于点D
∴∠ADC=∠BDC=90°
∵∠B=45°
∴∠BCD=∠B=45°
∴CD=BD
∵∠A=30°,AC=
∴CD=
∴BD=CD=
由勾股定理得AD=
∴AB=AD+BD=
8、
9、75°或15°
如图所示:
(1),∴
,∴
∴
(2),∴
,∴
∴
∴
10、解:∵
∴△ABD和△ACD都是直角三角形
在Rt△ABD中,,AB=4
∴,
在Rt△ACD中,
∴
∴BC的长为
11、解:∵
∴△BCD和△ABC是直角三角形
在Rt△BCD中,,
∴
在Rt△ABC中,
∴
12、解:(1)∵
∴△AED是直角三角形
在Rt△AED中,AE=6,
∴,
∵BD平分,,
∴CD=DE=8
(2)由(1)得AD=10,CD=8
∴AC=AD+CD=10+8=18
在△ADE与△ABC中,
∵
∴△ADE∽△ABC
∴
即
∴BC=24
∴
13、解:(1)如图,连接BD,设BC的垂直平分线交BC于点F
∴BD=CD
C△ABD=AB+AD+BD=AB+AD+CD=AB+AC
∵AB=CE
∴C△ABD=AB+AC=CE+AC=AE=1
∴△ABD的周长为1。
(2)∵
∴设AD=x,则BD=3x
∵BD=CD
∴AC=AD+CD=x+3x=4x
在Rt△ABD中,
∴
三、
1、(1)证明:∵tan∠ABD=,cos∠DAC=,且tan∠ABD=cos∠DAC
∴
∴AC=BD
(2)解:由sinC=,可设AD=12k,AC=13k,k>0,∴DC==5k
由(1)知BD=AC=13k
∴BC=13k+5k=18k
∵BC=12
∴k=,∴AD=12×=8
2、解:(1)过点A作BD的垂线交BD的延长线于点E
在Rt△ABE中,
∵
∴AB=2AE,
在Rt△ADE中,
∵
∴DE=AE
∴BD=BE-DE=
∴
(2)如图,在AB上取一点E,使得DB=DE,连接EC。
∵DB=DE
∴
∴
∵DB=DC=DE
∴△DEC是等边三角形
∴
∴
∵
∴
∵
∴
∴ED=EA=EC
∵
∴
∴
四、
1、解:(1)(方法一)连接OB、OC,过点O作OE⊥BC于点E。
∵OE⊥BC,BC=
∴BE=EC=
在Rt△OBE中,OB=2,
∴sin∠BOE=
∴∠BOE=60°,∠BOC=120°
∴∠BAC=∠BOC=60°
(方法二)连接BO并延长,交☉O于点D,连接CD。
∵BD是直径
∴BD=4,∠DCB=90°
在Rt△DBC中,sin∠BDC=
∴∠BDC=60°
∴∠BAC=∠BDC=60°
(2)∵△ABC的边BC的长不变
∴当BC边上的高最大时,△ABC的面积最大,此时点A应落在优弧BC的中点处
过点O作OE⊥BC于E,延长EO交☉O于点A,则A为优弧BC的中点。连接AB、AC,则AB=AC,
∠BAE=∠BAC=30°
在Rt△ABE中,
∵BE=,∠BAE=30°
∴AE=
∴S△ABC=
即△ABC面积的最大值是。
2、(1)证明:∵BC是☉O的直径,
∴,即
∵OA=OC
∴
∵CA平分
∴
∴
∴AO∥DE
∴
(2)解:延长AO交BD于点H,延长DF交☉O于点G,连接BG,过点O作于点T
∵
∴设
在Rt△BOH中,
解得
∴
∵BG是直径
∴
∴AH∥GB
∴△DHO∽△DBG,△GBF∽△OAF
∴
∴
∴
∵
∴
∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【双减—同步分层作业】28.2.1解直角三角形
一、知识梳理
1、在△ABC中,,那么AC的长为________
2、如图,△ABC的顶点是正方形网格的格点,则cosC=________
二、夯实基础(必做题)
1 2 3
1、如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AB=2米,则点P到直线AB距离PC为( )
A.3米 B.米 C.2米 D.1米
2、如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE∶EB=4∶1,EF⊥AC于F,连接FB,则tan∠CFB的值等于( )
A. B. C. D.
3、已知Rt△ABC的两条直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
A. B. C. D.
4 5 6 7
4、如图,在△ABC中,,于点D,。若E、F分别为AC、BC的中点,则EF的长为( )
A. B.2 C. D.
5、如图,在△ABC中,∠C=90°,AC=5 cm,,∠BAC的平分线交BC于点D,AD=cm,则
BC= cm.
6、小敏想知道校园内一棵大树的高度,如图,她测得CB=10 m,∠C=50°,请你帮她算出树高AB约为
m.
7、如图,在△ABC中,∠A=30°,∠B=45°,AC=,则AB的长为 .
8、如图,在Rt△ABC中,,CD是AB边上的中线,若CD=5,BC=6,则cos=______
9、已知AD是△ABC的高,CD=1,AD=BD=,则=______
10、如图,在△ABC中,,AB=4,于点D且,求BC的长。
11、如图,△ABC中,,D是AC上一点,,,求AB的长。
12、如图,在△ABC中,,点D、E分别在AC、AB上,BD平分,于点E。AE=6,。
(1)求CD的长;
(2)求的值。
13、如图,在Rt△ABC中,,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB。
(1)若AE=1,求△ABD的周长;
(2)若,求的值。
三、能力提升(中等生加练题)
1、如图,在△ABC中,AD是边BC上的高,tan∠ABD=cos∠DAC。
(1)求证:AC=BD;
(2)若sin C=,BC=12,求AD的长。
2、如图,在△ABC中,AD是中线,。
(1)求的值;
(2)求的值。
四、拓展训练(尖子生加练题)
1、如图,已知☉O的半径为2,弦BC的长为,点A为弦BC所对优弧上任意一点(B、C两点除外)。求:
(1)∠BAC的度数;
(2)△ABC面积的最大值。
2、如图,已知BC是☉O的直径,CA平分,延长EC交☉O于点D,连接DO并延长交AB于点F。
(1)求证:;
(2)已知,求。
【参考答案】
一、
1、6
2、
二、
1、B
2、C
3、C
4、B
5、12 AB=BC·tanC=10×tan50°≈12(m)
6、26
7、 如图,过点C作CD⊥AB于点D
∴∠ADC=∠BDC=90°
∵∠B=45°
∴∠BCD=∠B=45°
∴CD=BD
∵∠A=30°,AC=
∴CD=
∴BD=CD=
由勾股定理得AD=
∴AB=AD+BD=
8、
9、75°或15°
如图所示:
(1),∴
,∴
∴
(2),∴
,∴
∴
∴
10、解:∵
∴△ABD和△ACD都是直角三角形
在Rt△ABD中,,AB=4
∴,
在Rt△ACD中,
∴
∴BC的长为
11、解:∵
∴△BCD和△ABC是直角三角形
在Rt△BCD中,,
∴
在Rt△ABC中,
∴
12、解:(1)∵
∴△AED是直角三角形
在Rt△AED中,AE=6,
∴,
∵BD平分,,
∴CD=DE=8
(2)由(1)得AD=10,CD=8
∴AC=AD+CD=10+8=18
在△ADE与△ABC中,
∵
∴△ADE∽△ABC
∴
即
∴BC=24
∴
13、解:(1)如图,连接BD,设BC的垂直平分线交BC于点F
∴BD=CD
C△ABD=AB+AD+BD=AB+AD+CD=AB+AC
∵AB=CE
∴C△ABD=AB+AC=CE+AC=AE=1
∴△ABD的周长为1。
(2)∵
∴设AD=x,则BD=3x
∵BD=CD
∴AC=AD+CD=x+3x=4x
在Rt△ABD中,
∴
三、
1、(1)证明:∵tan∠ABD=,cos∠DAC=,且tan∠ABD=cos∠DAC
∴
∴AC=BD
(2)解:由sinC=,可设AD=12k,AC=13k,k>0,∴DC==5k
由(1)知BD=AC=13k
∴BC=13k+5k=18k
∵BC=12
∴k=,∴AD=12×=8
2、解:(1)过点A作BD的垂线交BD的延长线于点E
在Rt△ABE中,
∵
∴AB=2AE,
在Rt△ADE中,
∵
∴DE=AE
∴BD=BE-DE=
∴
(2)如图,在AB上取一点E,使得DB=DE,连接EC。
∵DB=DE
∴
∴
∵DB=DC=DE
∴△DEC是等边三角形
∴
∴
∵
∴
∵
∴
∴ED=EA=EC
∵
∴
∴
四、
1、解:(1)(方法一)连接OB、OC,过点O作OE⊥BC于点E。
∵OE⊥BC,BC=
∴BE=EC=
在Rt△OBE中,OB=2,
∴sin∠BOE=
∴∠BOE=60°,∠BOC=120°
∴∠BAC=∠BOC=60°
(方法二)连接BO并延长,交☉O于点D,连接CD。
∵BD是直径
∴BD=4,∠DCB=90°
在Rt△DBC中,sin∠BDC=
∴∠BDC=60°
∴∠BAC=∠BDC=60°
(2)∵△ABC的边BC的长不变
∴当BC边上的高最大时,△ABC的面积最大,此时点A应落在优弧BC的中点处
过点O作OE⊥BC于E,延长EO交☉O于点A,则A为优弧BC的中点。连接AB、AC,则AB=AC,
∠BAE=∠BAC=30°
在Rt△ABE中,
∵BE=,∠BAE=30°
∴AE=
∴S△ABC=
即△ABC面积的最大值是。
2、(1)证明:∵BC是☉O的直径,
∴,即
∵OA=OC
∴
∵CA平分
∴
∴
∴AO∥DE
∴
(2)解:延长AO交BD于点H,延长DF交☉O于点G,连接BG,过点O作于点T
∵
∴设
在Rt△BOH中,
解得
∴
∵BG是直径
∴
∴AH∥GB
∴△DHO∽△DBG,△GBF∽△OAF
∴
∴
∴
∵
∴
∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
