2021-2022学年北师大版七年级下册数学开学摸底考试模拟卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级下册数学开学摸底考试模拟卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 244.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览




文档简介
2021-2022学年七年级下册数学开学摸底考试模拟卷
时间:120分钟;满分:120分
一、选择题(本大题10小题,每小题3分,共30分〉在每小题列出的四个选项中,只有—个是正确的.
1.(本题3分)对于多项式2x2﹣3x﹣5,下列说法错误的是( )
A.它是二次三项式 B.最高次项的系数是2
C.2x2和3x是同类项 D.各项分别是2x2,﹣3x,﹣5
2.(本题3分)下列几何体中,不是柱体的是( )
A. B. C. D.
3.(本题3分)丁丁做了道计算题:①;②;③;④.请你帮他检查一下,他一共做对了( )
A.道 B.道 C.道 D.道
4.(本题3分)十边形中过其中一个顶点有( )条对角线.
A.7 B.8 C.9 D.10
5.(本题3分)若a与﹣1互为倒数,则|a﹣2|的值是( )
A.1 B.﹣1 C.3 D.﹣3
6.(本题3分)下列各数中最小的是( )
A.0 B.-1 C.1 D.
7.(本题3分)已知某公司去年的营业额约为四千零七十万元,则此营业额可表示为( )
A.4.07×元 B.4.07×元 C.4.07×元 D.4.07×元
8.(本题3分)如图,把一个边长为 16cm 的正方形纸片的四个角各剪去一个同样大小的正方形,然后把剩下的部分折成一个无盖的长方体盒子,当剪去的正方形的边长从 2 cm 变为 4cm后,长方体纸盒的容积( )cm3
A.减少了 32
B.减少了 80
C.增加了 32
D.增加了 80
9.(本题3分)下列调查中,适合于采用普查方式的是( )
A.调查央视“五一晚会”的收视率 B.了解外地游客对兴城旅游景点的印象
C.了解一批新型节能灯的使用寿命 D.了解某航班上的乘客是否都持有“绿色健康码”
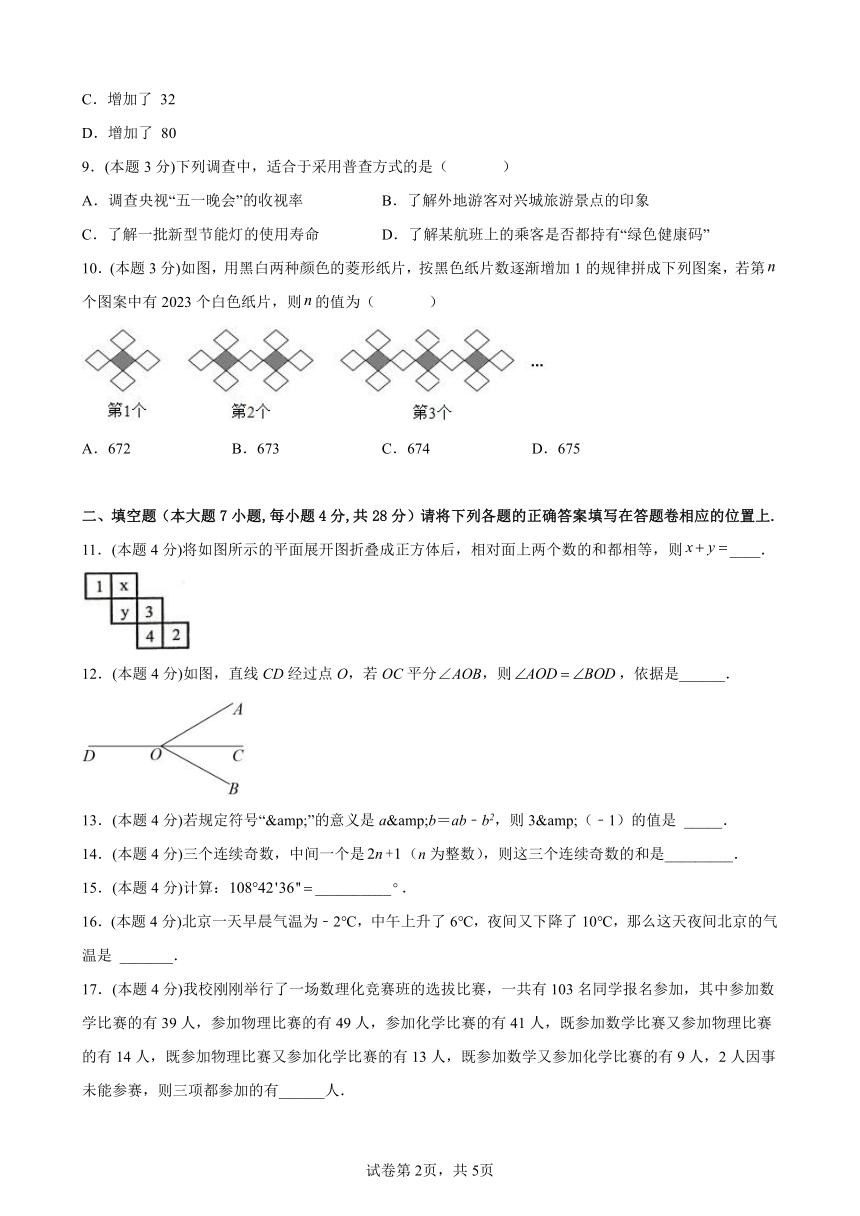
10.(本题3分)如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案,若第个图案中有2023个白色纸片,则的值为( )
A.672 B.673 C.674 D.675
二、填空题(本大题7小题,每小题4分,共28分)请将下列各题的正确答案填写在答题卷相应的位置上.
11.(本题4分)将如图所示的平面展开图折叠成正方体后,相对面上两个数的和都相等,则____.
12.(本题4分)如图,直线CD经过点O,若OC平分∠AOB,则,依据是______.
13.(本题4分)若规定符号“&”的意义是a&b=ab﹣b2,则3&(﹣1)的值是 _____.
14.(本题4分)三个连续奇数,中间一个是(n为整数),则这三个连续奇数的和是_________.
15.(本题4分)计算:__________.
16.(本题4分)北京一天早晨气温为﹣2℃,中午上升了6℃,夜间又下降了10℃,那么这天夜间北京的气温是 _______.
17.(本题4分)我校刚刚举行了一场数理化竞赛班的选拔比赛,一共有103名同学报名参加,其中参加数学比赛的有39人,参加物理比赛的有49人,参加化学比赛的有41人,既参加数学比赛又参加物理比赛的有14人,既参加物理比赛又参加化学比赛的有13人,既参加数学又参加化学比赛的有9人,2人因事未能参赛,则三项都参加的有______人.
三、解答题(本大题8小题,共62分)
18.(本题8分)计算:
(1)
(2)
19.(本题8分)解方程:
(1).
(2).
20.(本题6分)先化简,再求值:,其中,.
21.(本题7分)城固资源富集,享有“天然药库”的美誉,现有20筐药材,以每筐10千克为标准质量,超过的质量用正数表示,不足的质量用负数表示,结果记录如下:
与标准质量的差值(单位:千克) 0 0.4 0.5
筐数 1 4 2 3 2 8
(1)与标准质量相比,这20筐药材总计超过或不足多少千克?
(2)若这些药材平均以每千克15元的价格出售,则这20筐药材可卖多少元?
22.(本题8分)列方程解应用题
某建筑公司有甲.乙两个施工队,甲队的技术人员人数是乙队技术人员人数的2倍.今年公司进行人员调整,从甲施工队调出10名技术人员到乙施工队,结果两队技术人员相等了.
(1)原来甲.乙两施工队各有多少技术人员
(2)若这个建筑公司的人员人数比例是:领导:技术人员:工人=0.2:1:10,那么这个公司有多少人员?
23.(本题8分)如图,、两点把线段分成三部分,,为的中点.
(1)判断线段与的大小关系,说明理由.
(2)若,求的长.
24.(本题8分)虎林市各中小学正在加快推进特色课后服务的实施,某校为进一步增强教育的服务能力,初步组建了四种社团:A.体育、B.音乐、C.美术、D.科技.为了解学生最喜欢哪一种活动,并将调查结果绘制成了两幅不完整的统计图(如图①,图②),请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图补充完整;
(3)若该校共有学生1900人,请你估计该校喜欢科技项目的人数.
25.(本题9分)数轴上点A表示数﹣6,点B表示数18,动点P在数轴上从点A出发以每秒4个单位长度的速度向右运动,点P出发1秒钟后,动点Q以每秒6个单位长度的速度也从点A出发向右运动.设点P的运动时间为t(0≤t≤6).
(1)在运动过程中,点P表示的数为 ,点Q表示的数为 ;(用含t的代数式表示)
(2)当t的值为 时,点Q追上点P,此时点P对应的数是 ;
(3)动点Q出发后,求t为何值时,点P,Q,B三点中有一点到其余两点的距离相等.
试卷第1页,共3页
试卷第5页,共5页
参考答案:
1.C
【解析】解:多项式2x2-3x-5是二次三项式,故选项A不合题意;
多项式2x2-3x-5最高次项的系数是2,故选项B不合题意;
2x2和3x所含字母相同,但相同字母的指数不相同,不是同类项,故选项C符合题意;
多项式2x2-3x-5各项分别是2x2,-3x,-5,故选项D不合题意;
故选:C.
2.D
【解析】解:A圆柱是柱体,C三棱柱是柱体,B长方体是四棱柱,D圆锥是锥体,
故选D.
3.A
【解析】∵,故①错误;
∵,故②错误;
∵,故③正确;
∵,故④错误,
故丁丁一共做对了1道.
故选:A.
4.A
【解析】解:十边形中过其中一个顶点有10-3=7条对角线,
故选:A.
5.C
【解析】解:∵a与﹣1互为倒数,
∴a=﹣1,
∴|a﹣2|=|﹣1﹣2|=3,
故选:C.
6.B
【解析】解:∵||=,| 1|=1,<1,
∴ 1< <0<1,
故最小的数是 1.
故选:B.
7.C
【解析】∵四千零七十万元=40700000元=4.07×元,
故选C.
8.A
【解析】解:由题意,剪去的正方形的边长为2 cm时,长方体容积为(16-2×2)2×2=288 cm3,
剪去的正方形的边长为4 cm时,长方体容积为(16-2×4)2×4=256cm3,
288-256=32 cm3,
∴当剪去的正方形的边长从 2 cm 变为 4cm后,长方体纸盒的容积减少了32 cm3,
故选:A.
9.D
【解析】A.调查央视“五一晚会”的收视率,适合抽样调查;
B.了解外地游客对兴城旅游景点的印象,适合抽样调查;
C.了解一批新型节能灯的使用寿命,适合抽样调查;
D.了解某航班上的乘客是否都持有“绿色健康码”,适合普查;
故选:D.
10.C
【解析】解:由图可知,
第1个图案中白色纸片的个数为:1+1×3=4,
第2个图案中白色纸片的个数为:1+2×3=7,
第3个图案中白色纸片的个数为:1+3×3=10,
…
第n个图案中白色纸片的个数为:1+3n,
由题意得,1+3n =2023
解得n=674
故选:C.
11.
【解析】解:由正方体的展开图的特点可得:
相对,相对,相对,
相对面上两个数的和都相等,
∴
解得:
∴
故答案为:
12.等角的补角相等
【解析】解:∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵∠AOC+∠AOD=180°,∠BOC+∠BOD=180°,
∴∠AOD=∠BOD(等角的补角相等),
故答案为:等角的补角相等.
13.-4
【解析】解:∵a&b=ab﹣b2,
∴原式=3×(﹣1)﹣(﹣1)2
=﹣3﹣1
=﹣3+(﹣1)
=﹣4.
故答案为:﹣4.
14.6n+3##3+6n
【解析】解:∵中间的一个是2n+1,
∴第一个为-2=2n-1,最后一个为+2=2n+3,则
三个数的和为(2n-1)+(2n+1)+(2n+3)=6n+3.
故答案为:6n+3.
15.
【解析】解:
.
故答案为:.
16.﹣6°C
【解析】解:﹣2+(+6)+(﹣10)
=-2+6-10
=﹣6(°C),
故答案为:﹣6°C.
17.8
【解析】解:设三项都参加的共有人,依题意有
,
解得.
故三项都参加的共有8人.
故答案为:8.
18.(1)38
(2)
【解析】(1)解:
=-16+54
=38;
(2)解:
=
=
=.
19.(1)
(2)
【解析】(1)
去括号得:6x-3=3x+1,
移项、合并得:3x=4,
系数化为1得:.
(2)
去分母得:4(x-10)=3x-8,
去括号得:4x-40=3x-8,
移项、合并得:x=32.
20.;
【解析】解:原式
.
当,时,原式.
21.(1)这20筐药材总计超过1.4千克
(2)这20筐药材可卖3021元
【解析】(1)解:(-0.8)×1+(-0.5)×4+(-0.3)×2+0×3+0.4×2+0.5×8,
=-0.8-2-0.6+0+0.8+4,
=1.4(千克),
所以这20筐药材总计超过1.4千克.
(2)解:(10×20+1.4)×15,
=201.4×15,
=3 021(元),
所以这20筐药材可卖3021元.
22.(1)甲队有40名技术人员,乙队有20名技术人员;(2)总人数是672;
【解析】解:(1)设乙队技术员有x人,则甲队技术人员为2x人,
列方程得2x-10=x+10,
解得x=20,
∴2x=40,
所以甲队有40名技术人员,乙队有20名技术人员;
(2)由(1)可知,这个公司的技术人员有:40+20=60(人),
∵这个建筑公司的人员人数比例是:领导:技术人员:工人=0.2:1:10,
∴这个公司的领导有:60×0.2=12(人),工人有:60×10=600(人),
∴这个公司一共有:12+60+600=672(人),
答:这个公司有672人.
23.(1),见解析
(2)50
【解析】(1).理由如下:
设AB=2 x,BC=5 x,CD=3 x,则AD=10 x,
∵M为AD的中点,
∴AM=DM=AD=5x,
∴CM=DM-CD=5x-3x=2x,
∴AB=CM;
(2)∵CM=10cm,CM=2x,
∴2 x=10,
解得x=5,
∴AD=10x=50cm.
24.(1)200人
(2)见解析
(3)380人
【解析】(1)∵扇形A所占百分比为:×100%=10%,且A的频数为20,
∴这次被调查的学生共有:20÷10%=200(人).
(2)∵这次被调查的学生共200人,
∴美术社团的人数为:200-20-80-40=60(人),补图如下:
(3)该校喜欢科技项目的人数:=380(人),
答:该校喜欢科技项目的有380人.
25.(1),;(2),;(3)t=3或t=时,P,Q,B三点中有一点到其余两点的距离相等
【解析】解:(1)∵点A表示数﹣6,动点P从点A出发以每秒4个单位长度的速度向右运动,
∴点P表示的数为﹣6+4t(0≤t≤6);
∵点P出发1秒钟后,动点Q以每秒6个单位长度的速度从点A出发向右运动,
∴点Q表示的数为﹣6+6(t﹣1),即﹣12+6t(1≤t≤6);
故答案为:﹣6+4t(0≤t≤6),﹣12+6t(1≤t≤6).
(2)当点Q追上点P时,则﹣6+4t=﹣12+6t,
解得t=3,
∴﹣6+4t=﹣6+4×3=6,
∴此时点P对应的数是6,
故答案为:3,6.
(3)当点Q追上点P时,点B到点P、点Q的距离相等,
由(2)得,t=3;
当点Q到点P、点B的距离相等时,则﹣12+6t﹣(﹣6+4t)=18﹣(﹣12+6t),
解得t=;
当点P到点B、点Q的距离相等时,则﹣6+4t﹣18=﹣12+6t﹣(﹣6+4t),
解得t=9,不符合题意,舍去,
综上所述,当t=3或t=时,P,Q,B三点中有一点到其余两点的距离相等.
答案第1页,共2页
答案第8页,共1页
时间:120分钟;满分:120分
一、选择题(本大题10小题,每小题3分,共30分〉在每小题列出的四个选项中,只有—个是正确的.
1.(本题3分)对于多项式2x2﹣3x﹣5,下列说法错误的是( )
A.它是二次三项式 B.最高次项的系数是2
C.2x2和3x是同类项 D.各项分别是2x2,﹣3x,﹣5
2.(本题3分)下列几何体中,不是柱体的是( )
A. B. C. D.
3.(本题3分)丁丁做了道计算题:①;②;③;④.请你帮他检查一下,他一共做对了( )
A.道 B.道 C.道 D.道
4.(本题3分)十边形中过其中一个顶点有( )条对角线.
A.7 B.8 C.9 D.10
5.(本题3分)若a与﹣1互为倒数,则|a﹣2|的值是( )
A.1 B.﹣1 C.3 D.﹣3
6.(本题3分)下列各数中最小的是( )
A.0 B.-1 C.1 D.
7.(本题3分)已知某公司去年的营业额约为四千零七十万元,则此营业额可表示为( )
A.4.07×元 B.4.07×元 C.4.07×元 D.4.07×元
8.(本题3分)如图,把一个边长为 16cm 的正方形纸片的四个角各剪去一个同样大小的正方形,然后把剩下的部分折成一个无盖的长方体盒子,当剪去的正方形的边长从 2 cm 变为 4cm后,长方体纸盒的容积( )cm3
A.减少了 32
B.减少了 80
C.增加了 32
D.增加了 80
9.(本题3分)下列调查中,适合于采用普查方式的是( )
A.调查央视“五一晚会”的收视率 B.了解外地游客对兴城旅游景点的印象
C.了解一批新型节能灯的使用寿命 D.了解某航班上的乘客是否都持有“绿色健康码”
10.(本题3分)如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案,若第个图案中有2023个白色纸片,则的值为( )
A.672 B.673 C.674 D.675
二、填空题(本大题7小题,每小题4分,共28分)请将下列各题的正确答案填写在答题卷相应的位置上.
11.(本题4分)将如图所示的平面展开图折叠成正方体后,相对面上两个数的和都相等,则____.
12.(本题4分)如图,直线CD经过点O,若OC平分∠AOB,则,依据是______.
13.(本题4分)若规定符号“&”的意义是a&b=ab﹣b2,则3&(﹣1)的值是 _____.
14.(本题4分)三个连续奇数,中间一个是(n为整数),则这三个连续奇数的和是_________.
15.(本题4分)计算:__________.
16.(本题4分)北京一天早晨气温为﹣2℃,中午上升了6℃,夜间又下降了10℃,那么这天夜间北京的气温是 _______.
17.(本题4分)我校刚刚举行了一场数理化竞赛班的选拔比赛,一共有103名同学报名参加,其中参加数学比赛的有39人,参加物理比赛的有49人,参加化学比赛的有41人,既参加数学比赛又参加物理比赛的有14人,既参加物理比赛又参加化学比赛的有13人,既参加数学又参加化学比赛的有9人,2人因事未能参赛,则三项都参加的有______人.
三、解答题(本大题8小题,共62分)
18.(本题8分)计算:
(1)
(2)
19.(本题8分)解方程:
(1).
(2).
20.(本题6分)先化简,再求值:,其中,.
21.(本题7分)城固资源富集,享有“天然药库”的美誉,现有20筐药材,以每筐10千克为标准质量,超过的质量用正数表示,不足的质量用负数表示,结果记录如下:
与标准质量的差值(单位:千克) 0 0.4 0.5
筐数 1 4 2 3 2 8
(1)与标准质量相比,这20筐药材总计超过或不足多少千克?
(2)若这些药材平均以每千克15元的价格出售,则这20筐药材可卖多少元?
22.(本题8分)列方程解应用题
某建筑公司有甲.乙两个施工队,甲队的技术人员人数是乙队技术人员人数的2倍.今年公司进行人员调整,从甲施工队调出10名技术人员到乙施工队,结果两队技术人员相等了.
(1)原来甲.乙两施工队各有多少技术人员
(2)若这个建筑公司的人员人数比例是:领导:技术人员:工人=0.2:1:10,那么这个公司有多少人员?
23.(本题8分)如图,、两点把线段分成三部分,,为的中点.
(1)判断线段与的大小关系,说明理由.
(2)若,求的长.
24.(本题8分)虎林市各中小学正在加快推进特色课后服务的实施,某校为进一步增强教育的服务能力,初步组建了四种社团:A.体育、B.音乐、C.美术、D.科技.为了解学生最喜欢哪一种活动,并将调查结果绘制成了两幅不完整的统计图(如图①,图②),请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图补充完整;
(3)若该校共有学生1900人,请你估计该校喜欢科技项目的人数.
25.(本题9分)数轴上点A表示数﹣6,点B表示数18,动点P在数轴上从点A出发以每秒4个单位长度的速度向右运动,点P出发1秒钟后,动点Q以每秒6个单位长度的速度也从点A出发向右运动.设点P的运动时间为t(0≤t≤6).
(1)在运动过程中,点P表示的数为 ,点Q表示的数为 ;(用含t的代数式表示)
(2)当t的值为 时,点Q追上点P,此时点P对应的数是 ;
(3)动点Q出发后,求t为何值时,点P,Q,B三点中有一点到其余两点的距离相等.
试卷第1页,共3页
试卷第5页,共5页
参考答案:
1.C
【解析】解:多项式2x2-3x-5是二次三项式,故选项A不合题意;
多项式2x2-3x-5最高次项的系数是2,故选项B不合题意;
2x2和3x所含字母相同,但相同字母的指数不相同,不是同类项,故选项C符合题意;
多项式2x2-3x-5各项分别是2x2,-3x,-5,故选项D不合题意;
故选:C.
2.D
【解析】解:A圆柱是柱体,C三棱柱是柱体,B长方体是四棱柱,D圆锥是锥体,
故选D.
3.A
【解析】∵,故①错误;
∵,故②错误;
∵,故③正确;
∵,故④错误,
故丁丁一共做对了1道.
故选:A.
4.A
【解析】解:十边形中过其中一个顶点有10-3=7条对角线,
故选:A.
5.C
【解析】解:∵a与﹣1互为倒数,
∴a=﹣1,
∴|a﹣2|=|﹣1﹣2|=3,
故选:C.
6.B
【解析】解:∵||=,| 1|=1,<1,
∴ 1< <0<1,
故最小的数是 1.
故选:B.
7.C
【解析】∵四千零七十万元=40700000元=4.07×元,
故选C.
8.A
【解析】解:由题意,剪去的正方形的边长为2 cm时,长方体容积为(16-2×2)2×2=288 cm3,
剪去的正方形的边长为4 cm时,长方体容积为(16-2×4)2×4=256cm3,
288-256=32 cm3,
∴当剪去的正方形的边长从 2 cm 变为 4cm后,长方体纸盒的容积减少了32 cm3,
故选:A.
9.D
【解析】A.调查央视“五一晚会”的收视率,适合抽样调查;
B.了解外地游客对兴城旅游景点的印象,适合抽样调查;
C.了解一批新型节能灯的使用寿命,适合抽样调查;
D.了解某航班上的乘客是否都持有“绿色健康码”,适合普查;
故选:D.
10.C
【解析】解:由图可知,
第1个图案中白色纸片的个数为:1+1×3=4,
第2个图案中白色纸片的个数为:1+2×3=7,
第3个图案中白色纸片的个数为:1+3×3=10,
…
第n个图案中白色纸片的个数为:1+3n,
由题意得,1+3n =2023
解得n=674
故选:C.
11.
【解析】解:由正方体的展开图的特点可得:
相对,相对,相对,
相对面上两个数的和都相等,
∴
解得:
∴
故答案为:
12.等角的补角相等
【解析】解:∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵∠AOC+∠AOD=180°,∠BOC+∠BOD=180°,
∴∠AOD=∠BOD(等角的补角相等),
故答案为:等角的补角相等.
13.-4
【解析】解:∵a&b=ab﹣b2,
∴原式=3×(﹣1)﹣(﹣1)2
=﹣3﹣1
=﹣3+(﹣1)
=﹣4.
故答案为:﹣4.
14.6n+3##3+6n
【解析】解:∵中间的一个是2n+1,
∴第一个为-2=2n-1,最后一个为+2=2n+3,则
三个数的和为(2n-1)+(2n+1)+(2n+3)=6n+3.
故答案为:6n+3.
15.
【解析】解:
.
故答案为:.
16.﹣6°C
【解析】解:﹣2+(+6)+(﹣10)
=-2+6-10
=﹣6(°C),
故答案为:﹣6°C.
17.8
【解析】解:设三项都参加的共有人,依题意有
,
解得.
故三项都参加的共有8人.
故答案为:8.
18.(1)38
(2)
【解析】(1)解:
=-16+54
=38;
(2)解:
=
=
=.
19.(1)
(2)
【解析】(1)
去括号得:6x-3=3x+1,
移项、合并得:3x=4,
系数化为1得:.
(2)
去分母得:4(x-10)=3x-8,
去括号得:4x-40=3x-8,
移项、合并得:x=32.
20.;
【解析】解:原式
.
当,时,原式.
21.(1)这20筐药材总计超过1.4千克
(2)这20筐药材可卖3021元
【解析】(1)解:(-0.8)×1+(-0.5)×4+(-0.3)×2+0×3+0.4×2+0.5×8,
=-0.8-2-0.6+0+0.8+4,
=1.4(千克),
所以这20筐药材总计超过1.4千克.
(2)解:(10×20+1.4)×15,
=201.4×15,
=3 021(元),
所以这20筐药材可卖3021元.
22.(1)甲队有40名技术人员,乙队有20名技术人员;(2)总人数是672;
【解析】解:(1)设乙队技术员有x人,则甲队技术人员为2x人,
列方程得2x-10=x+10,
解得x=20,
∴2x=40,
所以甲队有40名技术人员,乙队有20名技术人员;
(2)由(1)可知,这个公司的技术人员有:40+20=60(人),
∵这个建筑公司的人员人数比例是:领导:技术人员:工人=0.2:1:10,
∴这个公司的领导有:60×0.2=12(人),工人有:60×10=600(人),
∴这个公司一共有:12+60+600=672(人),
答:这个公司有672人.
23.(1),见解析
(2)50
【解析】(1).理由如下:
设AB=2 x,BC=5 x,CD=3 x,则AD=10 x,
∵M为AD的中点,
∴AM=DM=AD=5x,
∴CM=DM-CD=5x-3x=2x,
∴AB=CM;
(2)∵CM=10cm,CM=2x,
∴2 x=10,
解得x=5,
∴AD=10x=50cm.
24.(1)200人
(2)见解析
(3)380人
【解析】(1)∵扇形A所占百分比为:×100%=10%,且A的频数为20,
∴这次被调查的学生共有:20÷10%=200(人).
(2)∵这次被调查的学生共200人,
∴美术社团的人数为:200-20-80-40=60(人),补图如下:
(3)该校喜欢科技项目的人数:=380(人),
答:该校喜欢科技项目的有380人.
25.(1),;(2),;(3)t=3或t=时,P,Q,B三点中有一点到其余两点的距离相等
【解析】解:(1)∵点A表示数﹣6,动点P从点A出发以每秒4个单位长度的速度向右运动,
∴点P表示的数为﹣6+4t(0≤t≤6);
∵点P出发1秒钟后,动点Q以每秒6个单位长度的速度从点A出发向右运动,
∴点Q表示的数为﹣6+6(t﹣1),即﹣12+6t(1≤t≤6);
故答案为:﹣6+4t(0≤t≤6),﹣12+6t(1≤t≤6).
(2)当点Q追上点P时,则﹣6+4t=﹣12+6t,
解得t=3,
∴﹣6+4t=﹣6+4×3=6,
∴此时点P对应的数是6,
故答案为:3,6.
(3)当点Q追上点P时,点B到点P、点Q的距离相等,
由(2)得,t=3;
当点Q到点P、点B的距离相等时,则﹣12+6t﹣(﹣6+4t)=18﹣(﹣12+6t),
解得t=;
当点P到点B、点Q的距离相等时,则﹣6+4t﹣18=﹣12+6t﹣(﹣6+4t),
解得t=9,不符合题意,舍去,
综上所述,当t=3或t=时,P,Q,B三点中有一点到其余两点的距离相等.
答案第1页,共2页
答案第8页,共1页
同课章节目录
