2022年北师大版七年级数学下册1.5 平方差公式 课件(16张)
文档属性
| 名称 | 2022年北师大版七年级数学下册1.5 平方差公式 课件(16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 15:00:08 | ||
图片预览






文档简介
(共16张PPT)
1.5 平方差公式
学习目标
1.探索平方差公式的几何背景,培养数形结合的数学思想;
2.会运用平方差公式进行简单的简便运算,培养运算技能.
2、应用平方差公式的注意事项:
1)注意平方差公式的适用范围(前同号,后异号)
2)字母a、b可以是数,也可以是整式
3)注意计算过程中的符号和括号
1、设这个自然数为a,与它相邻的两个自然数为a-1,a+1,则有(a+1)(a-1)=a2-1.
导入新课
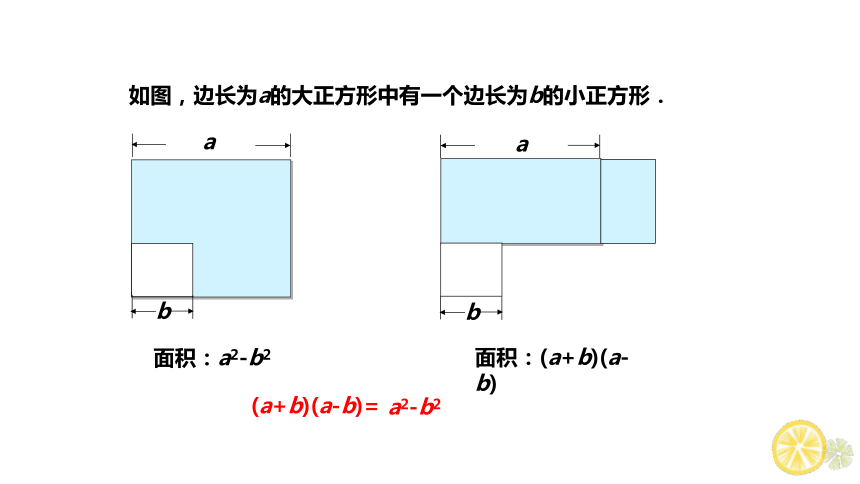
如图,边长为a的大正方形中有一个边长为b的小正方形.
a
b
a
b
面积:a2-b2
面积:(a+b)(a-b)
(a+b)(a-b)=
a2-b2
计算下列各组算式,并观察它们的特点.
7×9= 11×13= 79×81=
8×8= 12×12= 80×80=
63
64
143
144
6399
6400
1、从以上过程中,你发现了什么规律?
一个自然数的平方比它相邻两数的积大1.
2、你能用字母表示这一规律吗?
设这个自然数为a,与它相邻的两个自然数为a-1,a+1,
则有(a+1)(a-1)=a2-1.
探究学习
例1、用平方差公式进行计算:
(1) 103×97; (2) 118×122.
解:103×97
解:118×122
=(100+3)(100-3)
=1002-32
=(100+2)(100-2)
=1202-22
=9991
=14396
例2、利用平方差公式计算:
(1)20×19; (2)13.2×12.8.
解:(1)20 ×19
=(20+ )×(20- )
=202-() 2
=400-
=399
解:(2)13.2×12.8
=(13+0.2)×(13-0.2)
=132-0.22
=169-0.04
=168.96
例3、计算:
(1) (2)
解:(1)原式=19982-(1998-1)×(1998+1)
= 19982 -19982+1
=1
(2)原式=() ()()
= () ()
= ()
例4、公式的逆用
(1)(x+y)2-(x-y)2 (2)252-242
解:(1)(x+y)2-(x-y)2
=[(x+y)+(x-y)][(x+y)-(x-y)]
=2x·2y
=4xy
解:(2)252-242
=(25+24)(25-24)
=49
随堂练习
1.对于任意整数n,能整除代数式的整数是( ).
A.4 B.3 C.5 D.2
2. 在的计算中,第一步正确的是( ).
A. B.
C. D.
C
C
随堂练习
3.计算:
(1)704×696 ; (2)9.9 ×10.1
解:704×696
=(700+4)(700-4)
=7002-42
= 489984
解:9.9×10.1
=(10-0.1)(10+0.1)
=102-0.12
= 99.99
随堂练习
4. 利用乘法公式计算:
(1)计算:(2+1)·(22+1)·(24+1)·(28+1);
(2)计算:(3+1)·(32+1)·(34+1)·(38+1);
(3)计算:1002﹣992+982﹣972+…+22﹣12.
解:(1)原式=(2﹣1)·(2+1)·(22+1)·(24+1)·(28+1)
=(22﹣1)·(22+1)·(24+1)·(28+1)
=(24﹣1)·(24+1)·(28+1)
=(28﹣1)·(28+1)
=216﹣1
随堂练习
(2)原式=(3﹣1) ·(3+1) ·(32+1) ·(34+1) ·(38+1)
= (32﹣1) ·(32+1) ·(34+1) ·(38+1)
= (34﹣1) ·(34+1) ·(38+1)
= (38﹣1) ·(38+1)
= (316﹣1)
随堂练习
(3)原式=(1002﹣992)+(982﹣972)+…(+22﹣12)
=(1002﹣12)﹣(992﹣22)+(982﹣32)﹣…+(522﹣492)﹣(512﹣502)
=(100+1)×(100﹣1)﹣(99+2)×(99﹣2)+(98+3)×(98﹣3)﹣…+(52+49)×(52﹣49)﹣(50+51)×(51﹣50)
=101×99﹣101×97+101×95﹣…+101×3﹣101×1
=101×(99﹣97+85﹣…+3﹣1)
=101×(2+2+…+2)
=101×25×2
=5050.
课堂小结
1、平方差公式
(a+b)(a-b)=a2-b2
两数和与这两数差的积,等于它们的平方差.
2、应用平方差公式的注意事项:
(1)注意平方差公式的适用范围;
(2)字母a、b可以是数,也可以是整式;
(3)注意计算过程中的符号和括号.
1.5 平方差公式
学习目标
1.探索平方差公式的几何背景,培养数形结合的数学思想;
2.会运用平方差公式进行简单的简便运算,培养运算技能.
2、应用平方差公式的注意事项:
1)注意平方差公式的适用范围(前同号,后异号)
2)字母a、b可以是数,也可以是整式
3)注意计算过程中的符号和括号
1、设这个自然数为a,与它相邻的两个自然数为a-1,a+1,则有(a+1)(a-1)=a2-1.
导入新课
如图,边长为a的大正方形中有一个边长为b的小正方形.
a
b
a
b
面积:a2-b2
面积:(a+b)(a-b)
(a+b)(a-b)=
a2-b2
计算下列各组算式,并观察它们的特点.
7×9= 11×13= 79×81=
8×8= 12×12= 80×80=
63
64
143
144
6399
6400
1、从以上过程中,你发现了什么规律?
一个自然数的平方比它相邻两数的积大1.
2、你能用字母表示这一规律吗?
设这个自然数为a,与它相邻的两个自然数为a-1,a+1,
则有(a+1)(a-1)=a2-1.
探究学习
例1、用平方差公式进行计算:
(1) 103×97; (2) 118×122.
解:103×97
解:118×122
=(100+3)(100-3)
=1002-32
=(100+2)(100-2)
=1202-22
=9991
=14396
例2、利用平方差公式计算:
(1)20×19; (2)13.2×12.8.
解:(1)20 ×19
=(20+ )×(20- )
=202-() 2
=400-
=399
解:(2)13.2×12.8
=(13+0.2)×(13-0.2)
=132-0.22
=169-0.04
=168.96
例3、计算:
(1) (2)
解:(1)原式=19982-(1998-1)×(1998+1)
= 19982 -19982+1
=1
(2)原式=() ()()
= () ()
= ()
例4、公式的逆用
(1)(x+y)2-(x-y)2 (2)252-242
解:(1)(x+y)2-(x-y)2
=[(x+y)+(x-y)][(x+y)-(x-y)]
=2x·2y
=4xy
解:(2)252-242
=(25+24)(25-24)
=49
随堂练习
1.对于任意整数n,能整除代数式的整数是( ).
A.4 B.3 C.5 D.2
2. 在的计算中,第一步正确的是( ).
A. B.
C. D.
C
C
随堂练习
3.计算:
(1)704×696 ; (2)9.9 ×10.1
解:704×696
=(700+4)(700-4)
=7002-42
= 489984
解:9.9×10.1
=(10-0.1)(10+0.1)
=102-0.12
= 99.99
随堂练习
4. 利用乘法公式计算:
(1)计算:(2+1)·(22+1)·(24+1)·(28+1);
(2)计算:(3+1)·(32+1)·(34+1)·(38+1);
(3)计算:1002﹣992+982﹣972+…+22﹣12.
解:(1)原式=(2﹣1)·(2+1)·(22+1)·(24+1)·(28+1)
=(22﹣1)·(22+1)·(24+1)·(28+1)
=(24﹣1)·(24+1)·(28+1)
=(28﹣1)·(28+1)
=216﹣1
随堂练习
(2)原式=(3﹣1) ·(3+1) ·(32+1) ·(34+1) ·(38+1)
= (32﹣1) ·(32+1) ·(34+1) ·(38+1)
= (34﹣1) ·(34+1) ·(38+1)
= (38﹣1) ·(38+1)
= (316﹣1)
随堂练习
(3)原式=(1002﹣992)+(982﹣972)+…(+22﹣12)
=(1002﹣12)﹣(992﹣22)+(982﹣32)﹣…+(522﹣492)﹣(512﹣502)
=(100+1)×(100﹣1)﹣(99+2)×(99﹣2)+(98+3)×(98﹣3)﹣…+(52+49)×(52﹣49)﹣(50+51)×(51﹣50)
=101×99﹣101×97+101×95﹣…+101×3﹣101×1
=101×(99﹣97+85﹣…+3﹣1)
=101×(2+2+…+2)
=101×25×2
=5050.
课堂小结
1、平方差公式
(a+b)(a-b)=a2-b2
两数和与这两数差的积,等于它们的平方差.
2、应用平方差公式的注意事项:
(1)注意平方差公式的适用范围;
(2)字母a、b可以是数,也可以是整式;
(3)注意计算过程中的符号和括号.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
