人教版七年级数学 下册 第九章 9.3 一元一次不等式组 课件(共33张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第九章 9.3 一元一次不等式组 课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 08:22:23 | ||
图片预览










文档简介
(共33张PPT)
解一元一次不等式的基本步骤
1、去分母 (不等式的性质2)
2、去括号 (乘法分配律)
3、移项 (不等式的性质1)
4、合并同类项 (整式加减性质)
5、化系数为1 (不等式性质2,3)
知识回顾
情境引入
我90千克
我x千克
我40千克
嗨嗨,你知道小猪大约有多重?
探究新知
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
类比一元一次方程组的定义,想一想这构成了什么?
9.3 一元一次不等式组
人教版七年级数学 下册
1.通过具体操作,在解一元一次不等式组的过程中形成正确的解不等式组的思路与方法;(重点、难点)
2.掌握在数轴上正确表示一元一次不等式组的解集的方法.
学习目标
认真阅读课本中9.1.2 不等式的性质的内容,完成下面练习并体验知识点的形成过程。
自主研学
我们可以这样读书:
点信息,划精要 ,圈疑问
一边读一边做标识,
一边读一边做评注,
一边读一边做概括.
问题:一个长方形足球场的宽为70m,如果它的周长大于350m,面积小于7630m2,求这个足球场的长的取值范围,并判断这个足球场是否可以进行国际足球比赛
(注:用于国际足球比赛的足球场的长在100至110m之间,宽在64至75m之间).
目标导学一:一元一次不等式组的概念及解集
如果设足球场的长为x m,那么它的周长就是2(x+70)m,面积为70x m2.
根据已知条件,我们知道x的取值范围要使
2(x+70)>350 和70x<7630
这两个不等式同时成立.
为此,我们用大括号把上述两个不等式联立起来,得
2(x+70)>350 和70x<7630
像 这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个一元一次不等式组.
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
小试身手
思考:怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
归纳:我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
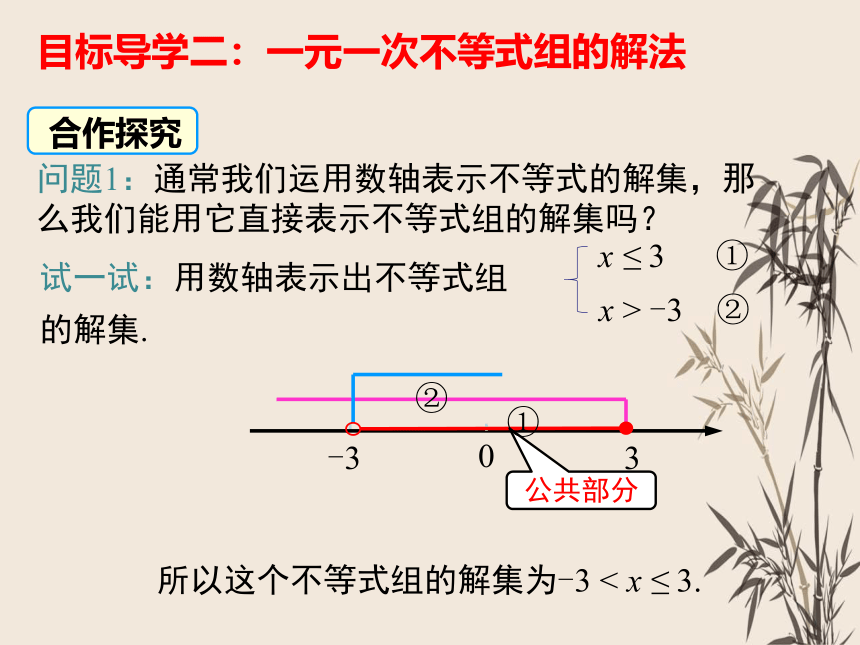
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试:用数轴表示出不等式组 的解集.
所以这个不等式组的解集为-3 < x ≤ 3.
x > -3 ②
x ≤ 3 ①
0
-3
3
公共部分
①
②
合作探究
目标导学二:一元一次不等式组的解法
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
a
a
a
b
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为 : x> b
(同大取大)
解集为 : x<a
(同小取小)
一元一次不等式组的解集的规律图析
(若当 a<b时 )
解集为: a<x<b
(大小小大中间找)
解集为:无解
(大大小小小无处找)
解不等式②,得
x <-3.
例1 解不等式组:
解: 解不等式①,得
x ≤ 3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是 x<-3.
典例精析
解一元一次不等式组的一般步骤:
分别求出各个不等式的解集
在数轴上表示出各个不等式的解集
找公共部分
用不等式表示出解集
通过本课时的学习,需要我们掌握:
方法归纳
2x-1>x-2
x+8>4x-1
例2:
解下列不等式组,并在数轴上表示出解集.
①
②
解:解不等式①,得 x>﹣1.
解不等式② ,得 x<3.
在数轴上表示不等式①, ②的解集
-1
3
所以这个不等式组的解集是 ﹣1知识应用
例3 求满足不等式的 所有整数解。
解法一
①
②
由①得 -4≤3-2x
2x≤3+4
x≤3.5
由②得 3-2x<8
-2x<8-3
x>-2.5
不等式①②的解集在数轴上表示为
-6 -5 -4 -3 -2 -1 0 1 2 3 4
∴不等式组的解集即原不等式的解集是-2.5整数解是:-2,-1,0,1,2,3
1.解不等式组:
解 解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
由图可以看出这两个不等式的解集没有公共部分.所以,这个不等式组无解.
0
-2
3
即学即练
2.不等式组 的解集为x<4,求a的取值范围.
x-a<0,
3x+2>5x-6
解:
解不等式①得x<a.
解不等式②得x<4.
因为此不等式组的解集为x<4,所以a≥4.
x-a<0, ①
3x+2>5x-6. ②
即学即练
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
目标导学三:一元一次不等式组的应用
3x>90
x+40<90
①
②
由①解得:x<50
由②解得:x>30
在数轴上表示不等式①,②的解集
0
50
30
∴这个不等式组的解集是:30解:
答:小猪的体重大约30至50千克.
列一元一次不等式组解实际问题的一般步骤:
(1)审题;
(2)设未知数,找不等量关系;
(3)根据不等关系列不等式组;
(4)解不等式组;
(5)检验并作答.
总结归纳
例:把一篮苹果分给几个学生,若每人分4个,则剩余3个;若每人分6个,则最后一个学生最多分2个,求学生人数和苹果分别是多少?
解:设学生有x个,则苹果有(4x+3)个,根据题意,得
(4x+3)-6(x-1)>0,
(4x+3)-6(x-1)≤2.
解不等式组,得3.5≤x<4.5
根据题意,x的值应是整数,所以x=4,则4x+3=19.
答:学生有4人,苹果有19个.
精典例题
一元一次不等式组
一元一次不等式组的概念
↓
利用公共部分确定不等式组的解集
在数轴上分别表示各个不等式的解集
解每个不等式
↓
一元一次不等式组的解集在数轴上的表示
一元一次不等式组的解集
解一元一次不等式组
→
↓
数形结合思想
类比思想
课堂小结
1.不等式组 的解集是( )
≥2,
≤2
A. ≥2,
D. =2.
B. ≤2,
C. 无解,
D
检测目标
C
2.不等式组 的整数解是( )
D. ≤1.
A. 0, 1 ,
B. 0 ,
C. 1,
≤1
检测目标
3.如图所示, 则其解集是( )
-1
2.5
4
B
A.
B.
C.
D.
≤4
≤4,
检测目标
4.不等式组 的解集在数轴上表示为( )
≥-2,
-5
-2
-5
-2
-5
-2
-5
-2
A.
D.
C.
B.
B
检测目标
D.无解.
A. x≥-2,
B. x≥-3 ,
C. -3<x≤-2,
5.不等式组 的解 集( )
≥-2,
A
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
解一元一次不等式的基本步骤
1、去分母 (不等式的性质2)
2、去括号 (乘法分配律)
3、移项 (不等式的性质1)
4、合并同类项 (整式加减性质)
5、化系数为1 (不等式性质2,3)
知识回顾
情境引入
我90千克
我x千克
我40千克
嗨嗨,你知道小猪大约有多重?
探究新知
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
类比一元一次方程组的定义,想一想这构成了什么?
9.3 一元一次不等式组
人教版七年级数学 下册
1.通过具体操作,在解一元一次不等式组的过程中形成正确的解不等式组的思路与方法;(重点、难点)
2.掌握在数轴上正确表示一元一次不等式组的解集的方法.
学习目标
认真阅读课本中9.1.2 不等式的性质的内容,完成下面练习并体验知识点的形成过程。
自主研学
我们可以这样读书:
点信息,划精要 ,圈疑问
一边读一边做标识,
一边读一边做评注,
一边读一边做概括.
问题:一个长方形足球场的宽为70m,如果它的周长大于350m,面积小于7630m2,求这个足球场的长的取值范围,并判断这个足球场是否可以进行国际足球比赛
(注:用于国际足球比赛的足球场的长在100至110m之间,宽在64至75m之间).
目标导学一:一元一次不等式组的概念及解集
如果设足球场的长为x m,那么它的周长就是2(x+70)m,面积为70x m2.
根据已知条件,我们知道x的取值范围要使
2(x+70)>350 和70x<7630
这两个不等式同时成立.
为此,我们用大括号把上述两个不等式联立起来,得
2(x+70)>350 和70x<7630
像 这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个一元一次不等式组.
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
小试身手
思考:怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
归纳:我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试:用数轴表示出不等式组 的解集.
所以这个不等式组的解集为-3 < x ≤ 3.
x > -3 ②
x ≤ 3 ①
0
-3
3
公共部分
①
②
合作探究
目标导学二:一元一次不等式组的解法
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
x
a
a
a
b
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为 : x> b
(同大取大)
解集为 : x<a
(同小取小)
一元一次不等式组的解集的规律图析
(若当 a<b时 )
解集为: a<x<b
(大小小大中间找)
解集为:无解
(大大小小小无处找)
解不等式②,得
x <-3.
例1 解不等式组:
解: 解不等式①,得
x ≤ 3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是 x<-3.
典例精析
解一元一次不等式组的一般步骤:
分别求出各个不等式的解集
在数轴上表示出各个不等式的解集
找公共部分
用不等式表示出解集
通过本课时的学习,需要我们掌握:
方法归纳
2x-1>x-2
x+8>4x-1
例2:
解下列不等式组,并在数轴上表示出解集.
①
②
解:解不等式①,得 x>﹣1.
解不等式② ,得 x<3.
在数轴上表示不等式①, ②的解集
-1
3
所以这个不等式组的解集是 ﹣1
例3 求满足不等式的 所有整数解。
解法一
①
②
由①得 -4≤3-2x
2x≤3+4
x≤3.5
由②得 3-2x<8
-2x<8-3
x>-2.5
不等式①②的解集在数轴上表示为
-6 -5 -4 -3 -2 -1 0 1 2 3 4
∴不等式组的解集即原不等式的解集是-2.5
1.解不等式组:
解 解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
由图可以看出这两个不等式的解集没有公共部分.所以,这个不等式组无解.
0
-2
3
即学即练
2.不等式组 的解集为x<4,求a的取值范围.
x-a<0,
3x+2>5x-6
解:
解不等式①得x<a.
解不等式②得x<4.
因为此不等式组的解集为x<4,所以a≥4.
x-a<0, ①
3x+2>5x-6. ②
即学即练
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
目标导学三:一元一次不等式组的应用
3x>90
x+40<90
①
②
由①解得:x<50
由②解得:x>30
在数轴上表示不等式①,②的解集
0
50
30
∴这个不等式组的解集是:30
答:小猪的体重大约30至50千克.
列一元一次不等式组解实际问题的一般步骤:
(1)审题;
(2)设未知数,找不等量关系;
(3)根据不等关系列不等式组;
(4)解不等式组;
(5)检验并作答.
总结归纳
例:把一篮苹果分给几个学生,若每人分4个,则剩余3个;若每人分6个,则最后一个学生最多分2个,求学生人数和苹果分别是多少?
解:设学生有x个,则苹果有(4x+3)个,根据题意,得
(4x+3)-6(x-1)>0,
(4x+3)-6(x-1)≤2.
解不等式组,得3.5≤x<4.5
根据题意,x的值应是整数,所以x=4,则4x+3=19.
答:学生有4人,苹果有19个.
精典例题
一元一次不等式组
一元一次不等式组的概念
↓
利用公共部分确定不等式组的解集
在数轴上分别表示各个不等式的解集
解每个不等式
↓
一元一次不等式组的解集在数轴上的表示
一元一次不等式组的解集
解一元一次不等式组
→
↓
数形结合思想
类比思想
课堂小结
1.不等式组 的解集是( )
≥2,
≤2
A. ≥2,
D. =2.
B. ≤2,
C. 无解,
D
检测目标
C
2.不等式组 的整数解是( )
D. ≤1.
A. 0, 1 ,
B. 0 ,
C. 1,
≤1
检测目标
3.如图所示, 则其解集是( )
-1
2.5
4
B
A.
B.
C.
D.
≤4
≤4,
检测目标
4.不等式组 的解集在数轴上表示为( )
≥-2,
-5
-2
-5
-2
-5
-2
-5
-2
A.
D.
C.
B.
B
检测目标
D.无解.
A. x≥-2,
B. x≥-3 ,
C. -3<x≤-2,
5.不等式组 的解 集( )
≥-2,
A
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
