鲁教版数学七下7.1二元一次方程组查漏补缺练习题(含答案)
文档属性
| 名称 | 鲁教版数学七下7.1二元一次方程组查漏补缺练习题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 220.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 13:19:14 | ||
图片预览
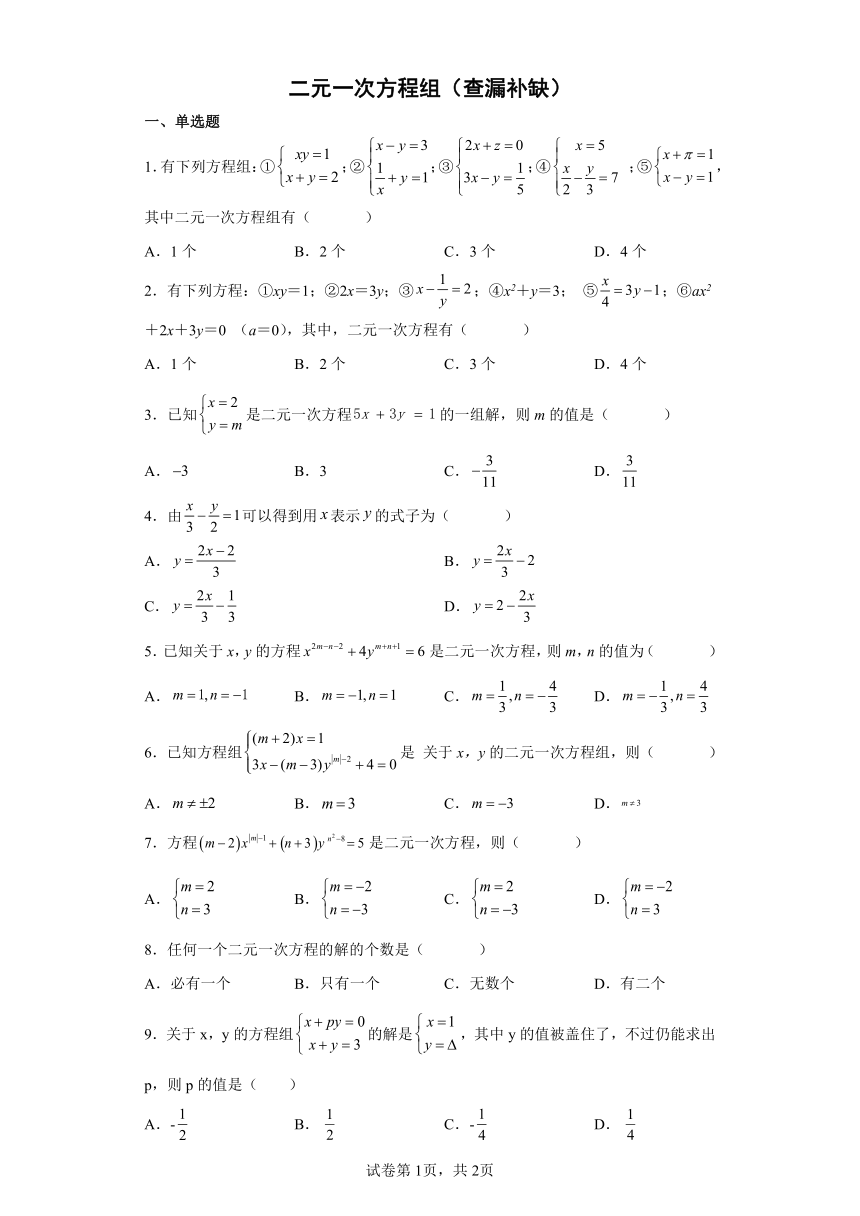




文档简介
二元一次方程组(查漏补缺)
一、单选题
1.有下列方程组:①;②;③;④ ;⑤,其中二元一次方程组有( )
A.1个 B.2个 C.3个 D.4个
2.有下列方程:①xy=1;②2x=3y;③;④x2+y=3; ⑤;⑥ax2+2x+3y=0 (a=0),其中,二元一次方程有( )
A.1个 B.2个 C.3个 D.4个
3.已知是二元一次方程的一组解,则m的值是( )
A. B.3 C. D.
4.由可以得到用表示的式子为( )
A. B.
C. D.
5.已知关于x,y的方程是二元一次方程,则m,n的值为( )
A. B. C. D.
6.已知方程组是 关于x,y的二元一次方程组,则( )
A. B. C. D.
7.方程是二元一次方程,则( )
A. B. C. D.
8.任何一个二元一次方程的解的个数是( )
A.必有一个 B.只有一个 C.无数个 D.有二个
9.关于x,y的方程组的解是,其中y的值被盖住了,不过仍能求出p,则p的值是( )
A.- B. C.- D.
二、填空题
10.方程组的解满足,则___________.
11.关于x或y的方程,当a________时,它是一元一次方程;当a________时,它是二元一次方程.
12.方程是关于x和y的二元一次方程,则_____,_______.
13.若是关于x和y的方程组的解,则________,________.
14.已知是方程3mx﹣y=﹣1的解,则m=_____.
15.若方程组无解,则_______.
16.已知,则________.
三、解答题
17.、为何值时,方程组的解是.
18.如果,是方程的一个解,求的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.C
3.A
【解析】
【分析】
把代入5x+3y=1即可求出m的值.
【详解】
把代入5x+3y=1,得
10+3m=1,
∴m=-3,
故选A.
【点睛】
本题考查了求二元一次方程的解,能使二元一次方程左右两边相等的未知数的值叫做二元一次方程的解.
4.B
【解析】
【分析】
先移项,后系数化为1,即可得.
【详解】
解:
移项,得,
系数化为1,得,
故选B.
【点睛】
本题考查了方程的基本运算技能,解题的关键是熟练掌握方程的基本运算技能.
5.A
【解析】
【分析】
根据二元一次方程的定义,得出关于m,n的方程组,求出答案.
【详解】
∵关于x、y的方程x2m﹣n﹣2+ym+n+1=6是二元一次方程,
∴,
解得.
故选:A.
【点睛】
此题考查了二元一次方程的定义和二元一次方程组的解法,熟练掌握二元一次方程的定义是解本题的关键.
6.C
【解析】
【分析】
二元一次方程组:由两个整式方程组成,两个方程一共含有两个未知数,且含未知数的项的最高次数是,这样的方程组是二元一次方程组,根据定义列方程或不等式,从而可得答案.
【详解】
解: 方程组是 关于x,y的二元一次方程组,
解得:
故选:
【点睛】
本题考查的是二元一次方程组的定义,掌握二元一次方程组的定义是解题的关键.
7.D
【解析】
【分析】
二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.
【详解】
由题意得且,
解得,,
故选D.
【点睛】
主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
8.C
【解析】
【分析】
根据二元一次方程的解的性质即可得.
【详解】
任何一个二元一次方程的解的个数是无数个,
故选:C.
【点睛】
本题考查了二元一次方程的解,掌握理解二元一次方程的解的性质是解题关键.
9.A
【解析】
【分析】
将x=1代入方程x+y=3求得y的值,将x、y的值代入x+py=0,可得关于p的方程,可求得p.
【详解】
解:根据题意,将x=1代入x+y=3,可得y=2,
将x=1,y=2代入x+py=0,得:1+2p=0,
解得:p=-,
故选:A.
【点睛】
本题主要考查二元一次方程组的解的概念,根据方程组的解会准确将方程的解代入是前提,严格遵循解方程的基本步骤求得方程的解是关键.
10.
【解析】
【分析】
根据x+y=0,可以得到x= y,代入方程组即可得到一个关于y和m的方程组,求得m的值.
【详解】
解:∵x+y=0,
∴x= y,代入方程组得: ,
解方程组得: .
故答案是: 5.
【点睛】
本题考查了方程组的解的定义,能使方程组中每个方程的左右两边相等的未知数的值即是方程组的解.解题的关键是要知道几个方程组之间解的关系.
11. 或 且
【解析】
【分析】
根据一元一次方程和二元一次方程的定义进行求解即可.
【详解】
解:∵,
∴,
∴当时,原方程为是一元一次方程,同理当时,原方程为是一元一次方程,
∴关于x或y的方程,当或时,它是一元一次方程;
∴当且时,原方程是二元一次方程,
故答案为:或;且.
【点睛】
本题主要考查了一元一次方程和二元一次方程的定义,解题的关键在于能够熟知定义.
12. 0
【解析】
【分析】
一般地.含有两个未知数,并且含有未知数的项的最高次数是一次的整式方程叫二元一次方程.根据定义列方程组,再解方程组即可得到答案.
【详解】
解: 方程是关于x和y的二元一次方程,
解得:
故答案为:
【点睛】
本题考查的是二元一次方程的定义,二元一次方程的解法,掌握二元一次方程的定义是解题的关键.
13. 1 2
【解析】
【分析】
把方程组的解代入方程组可得到关于a、b的方程组,解方程组即可.
【详解】
解:是关于、的方程组的解,
解得.
故答案为:1;2.
【点睛】
本题考查二元一次方程组的解和解二元一次方程组.理解方程组的解满足方程组中的每一个方程是解题的关键.
14.
【解析】
【分析】
把代入3mx﹣y=﹣1,再解方程即可得到答案.
【详解】
解: 是方程3mx﹣y=﹣1的解,
故答案为:
【点睛】
本题考查的是二元一次方程的解,掌握方程的解的含义是解题的关键.
15.6
【解析】
【分析】
方程组利用加减消元法消去x得到关于y的方程,由方程组无解求出a的值即可.
【详解】
,
,得.
∵方程组无解,
∴,即.
故答案为:6.
【点睛】
此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.
16.17
【解析】
【分析】
通过移项,得到;再将代入到代数式,即可得到答案.
【详解】
∵
∴
∴
故答案为:17.
【点睛】
本题考察了二元一次方程的知识;求解的关键是熟练掌握二元一次方程的性质,从而完成求解.
17.,
【解析】
【分析】
把解代入方程组得到关于a,b的方程组,求解即可;
【详解】
把,代入方程组得,
把①代入②,得,得,把代入①得.
【点睛】
本题主要考查了二元一次方程组的求解,准确计算是解题的关键.
18.
【解析】
【分析】
把x,y代入方程,即可得到k的值;
【详解】
当,时,则,,,.
【点睛】
本题主要考查了二元一次方程的求解,准确分析是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.有下列方程组:①;②;③;④ ;⑤,其中二元一次方程组有( )
A.1个 B.2个 C.3个 D.4个
2.有下列方程:①xy=1;②2x=3y;③;④x2+y=3; ⑤;⑥ax2+2x+3y=0 (a=0),其中,二元一次方程有( )
A.1个 B.2个 C.3个 D.4个
3.已知是二元一次方程的一组解,则m的值是( )
A. B.3 C. D.
4.由可以得到用表示的式子为( )
A. B.
C. D.
5.已知关于x,y的方程是二元一次方程,则m,n的值为( )
A. B. C. D.
6.已知方程组是 关于x,y的二元一次方程组,则( )
A. B. C. D.
7.方程是二元一次方程,则( )
A. B. C. D.
8.任何一个二元一次方程的解的个数是( )
A.必有一个 B.只有一个 C.无数个 D.有二个
9.关于x,y的方程组的解是,其中y的值被盖住了,不过仍能求出p,则p的值是( )
A.- B. C.- D.
二、填空题
10.方程组的解满足,则___________.
11.关于x或y的方程,当a________时,它是一元一次方程;当a________时,它是二元一次方程.
12.方程是关于x和y的二元一次方程,则_____,_______.
13.若是关于x和y的方程组的解,则________,________.
14.已知是方程3mx﹣y=﹣1的解,则m=_____.
15.若方程组无解,则_______.
16.已知,则________.
三、解答题
17.、为何值时,方程组的解是.
18.如果,是方程的一个解,求的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.C
3.A
【解析】
【分析】
把代入5x+3y=1即可求出m的值.
【详解】
把代入5x+3y=1,得
10+3m=1,
∴m=-3,
故选A.
【点睛】
本题考查了求二元一次方程的解,能使二元一次方程左右两边相等的未知数的值叫做二元一次方程的解.
4.B
【解析】
【分析】
先移项,后系数化为1,即可得.
【详解】
解:
移项,得,
系数化为1,得,
故选B.
【点睛】
本题考查了方程的基本运算技能,解题的关键是熟练掌握方程的基本运算技能.
5.A
【解析】
【分析】
根据二元一次方程的定义,得出关于m,n的方程组,求出答案.
【详解】
∵关于x、y的方程x2m﹣n﹣2+ym+n+1=6是二元一次方程,
∴,
解得.
故选:A.
【点睛】
此题考查了二元一次方程的定义和二元一次方程组的解法,熟练掌握二元一次方程的定义是解本题的关键.
6.C
【解析】
【分析】
二元一次方程组:由两个整式方程组成,两个方程一共含有两个未知数,且含未知数的项的最高次数是,这样的方程组是二元一次方程组,根据定义列方程或不等式,从而可得答案.
【详解】
解: 方程组是 关于x,y的二元一次方程组,
解得:
故选:
【点睛】
本题考查的是二元一次方程组的定义,掌握二元一次方程组的定义是解题的关键.
7.D
【解析】
【分析】
二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.
【详解】
由题意得且,
解得,,
故选D.
【点睛】
主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
8.C
【解析】
【分析】
根据二元一次方程的解的性质即可得.
【详解】
任何一个二元一次方程的解的个数是无数个,
故选:C.
【点睛】
本题考查了二元一次方程的解,掌握理解二元一次方程的解的性质是解题关键.
9.A
【解析】
【分析】
将x=1代入方程x+y=3求得y的值,将x、y的值代入x+py=0,可得关于p的方程,可求得p.
【详解】
解:根据题意,将x=1代入x+y=3,可得y=2,
将x=1,y=2代入x+py=0,得:1+2p=0,
解得:p=-,
故选:A.
【点睛】
本题主要考查二元一次方程组的解的概念,根据方程组的解会准确将方程的解代入是前提,严格遵循解方程的基本步骤求得方程的解是关键.
10.
【解析】
【分析】
根据x+y=0,可以得到x= y,代入方程组即可得到一个关于y和m的方程组,求得m的值.
【详解】
解:∵x+y=0,
∴x= y,代入方程组得: ,
解方程组得: .
故答案是: 5.
【点睛】
本题考查了方程组的解的定义,能使方程组中每个方程的左右两边相等的未知数的值即是方程组的解.解题的关键是要知道几个方程组之间解的关系.
11. 或 且
【解析】
【分析】
根据一元一次方程和二元一次方程的定义进行求解即可.
【详解】
解:∵,
∴,
∴当时,原方程为是一元一次方程,同理当时,原方程为是一元一次方程,
∴关于x或y的方程,当或时,它是一元一次方程;
∴当且时,原方程是二元一次方程,
故答案为:或;且.
【点睛】
本题主要考查了一元一次方程和二元一次方程的定义,解题的关键在于能够熟知定义.
12. 0
【解析】
【分析】
一般地.含有两个未知数,并且含有未知数的项的最高次数是一次的整式方程叫二元一次方程.根据定义列方程组,再解方程组即可得到答案.
【详解】
解: 方程是关于x和y的二元一次方程,
解得:
故答案为:
【点睛】
本题考查的是二元一次方程的定义,二元一次方程的解法,掌握二元一次方程的定义是解题的关键.
13. 1 2
【解析】
【分析】
把方程组的解代入方程组可得到关于a、b的方程组,解方程组即可.
【详解】
解:是关于、的方程组的解,
解得.
故答案为:1;2.
【点睛】
本题考查二元一次方程组的解和解二元一次方程组.理解方程组的解满足方程组中的每一个方程是解题的关键.
14.
【解析】
【分析】
把代入3mx﹣y=﹣1,再解方程即可得到答案.
【详解】
解: 是方程3mx﹣y=﹣1的解,
故答案为:
【点睛】
本题考查的是二元一次方程的解,掌握方程的解的含义是解题的关键.
15.6
【解析】
【分析】
方程组利用加减消元法消去x得到关于y的方程,由方程组无解求出a的值即可.
【详解】
,
,得.
∵方程组无解,
∴,即.
故答案为:6.
【点睛】
此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.
16.17
【解析】
【分析】
通过移项,得到;再将代入到代数式,即可得到答案.
【详解】
∵
∴
∴
故答案为:17.
【点睛】
本题考察了二元一次方程的知识;求解的关键是熟练掌握二元一次方程的性质,从而完成求解.
17.,
【解析】
【分析】
把解代入方程组得到关于a,b的方程组,求解即可;
【详解】
把,代入方程组得,
把①代入②,得,得,把代入①得.
【点睛】
本题主要考查了二元一次方程组的求解,准确计算是解题的关键.
18.
【解析】
【分析】
把x,y代入方程,即可得到k的值;
【详解】
当,时,则,,,.
【点睛】
本题主要考查了二元一次方程的求解,准确分析是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
