2021-2022学年鲁教版(五四制)八年级数学下册6.1 菱形的性质与判定第1课时 菱形的性质 同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.1 菱形的性质与判定第1课时 菱形的性质 同步练习(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 148.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 08:29:56 | ||
图片预览


文档简介
1 菱形的性质与判定
第1课时 菱形的性质
自 主 预 习
1.有一组 的平行四边形叫做菱形.
2.菱形既是轴对称图形,也是中心对称图形,其对称轴是 ,对称中心为 ;
3.菱形的四条边都 ;菱形的对角线 .
4.(想一想)菱形与平行四边形的对应元素之间有什么联系和区别?
5.(做一做)如图,在菱形ABCD中,BD=6,AC=8,求菱形的周长.
随 堂 学 练
知识通关
知识点1 菱形的概念及菱形的性质(边)
1.如图,菱形ABCD中,BE⊥AD,BF⊥CD,F、F为垂足,AE=ED,则∠EBF等于()
A.75° B.60° C.50° D.45°
2.如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是( )
A.25 B.20 C.15 D.10
知识点2菱形的性质(对角线)
3. 如图所示,菱形ABCD在平面直角坐标系中,∠ABC=60°,点A的坐标为(0,),则B、C、D三点的坐标为_______.
4.(昆明)如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论:①AC⊥BD;②OA=OB;③∠ADB=∠CDB;④△ABC是等边三角形,其中一定成立的是( )
A.①② B.③④ C.②③ D.①③
课堂达标
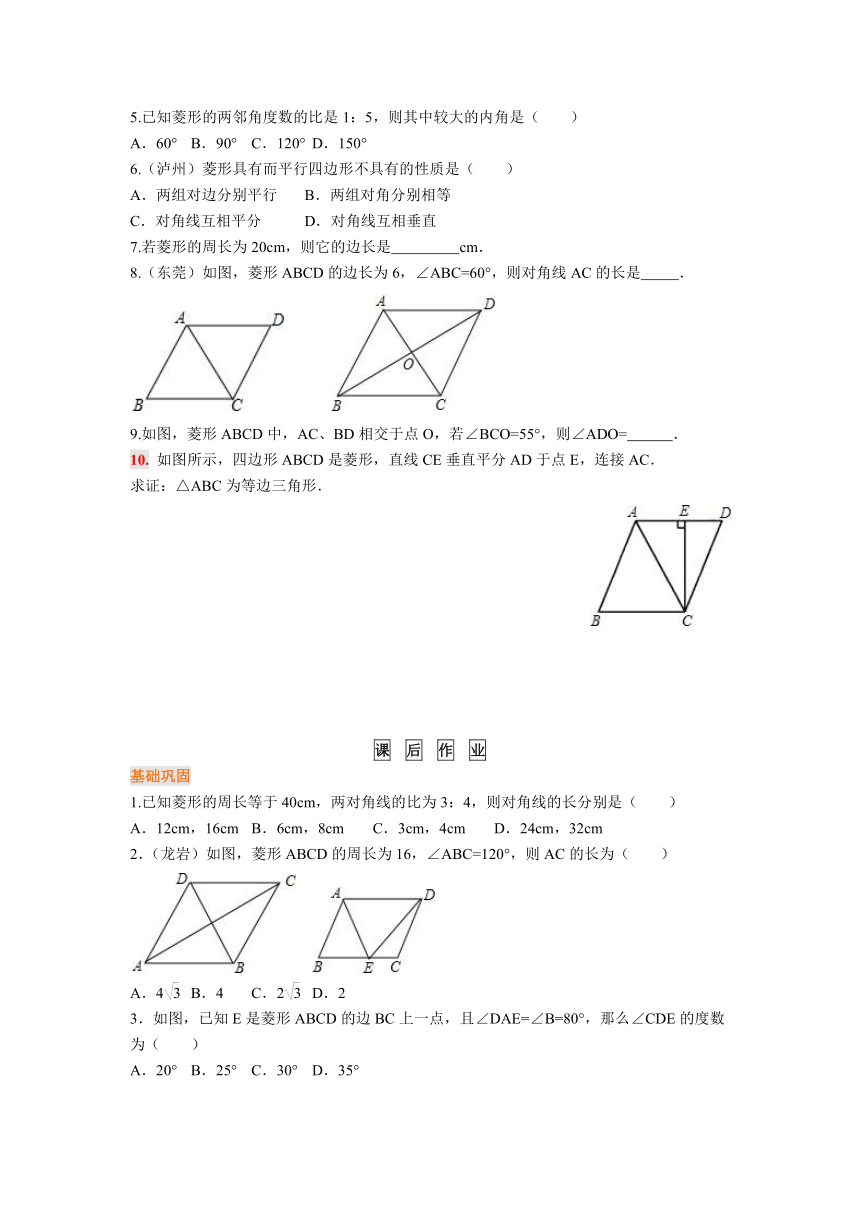
5.已知菱形的两邻角度数的比是1:5,则其中较大的内角是( )
A.60° B.90° C.120° D.150°
6.(泸州)菱形具有而平行四边形不具有的性质是( )
A.两组对边分别平行 B.两组对角分别相等
C.对角线互相平分 D.对角线互相垂直
7.若菱形的周长为20cm,则它的边长是 cm.
8.(东莞)如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长是 .
9.如图,菱形ABCD中,AC、BD相交于点O,若∠BCO=55°,则∠ADO= .
10. 如图所示,四边形ABCD是菱形,直线CE垂直平分AD于点E,连接AC.
求证:△ABC为等边三角形.
课 后 作 业
基础巩固
1.已知菱形的周长等于40cm,两对角线的比为3:4,则对角线的长分别是( )
A.12cm,16cm B.6cm,8cm C.3cm,4cm D.24cm,32cm
2.(龙岩)如图,菱形ABCD的周长为16,∠ABC=120°,则AC的长为( )
A.4 B.4 C.2 D.2
3.如图,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( )
A.20° B.25° C.30° D.35°
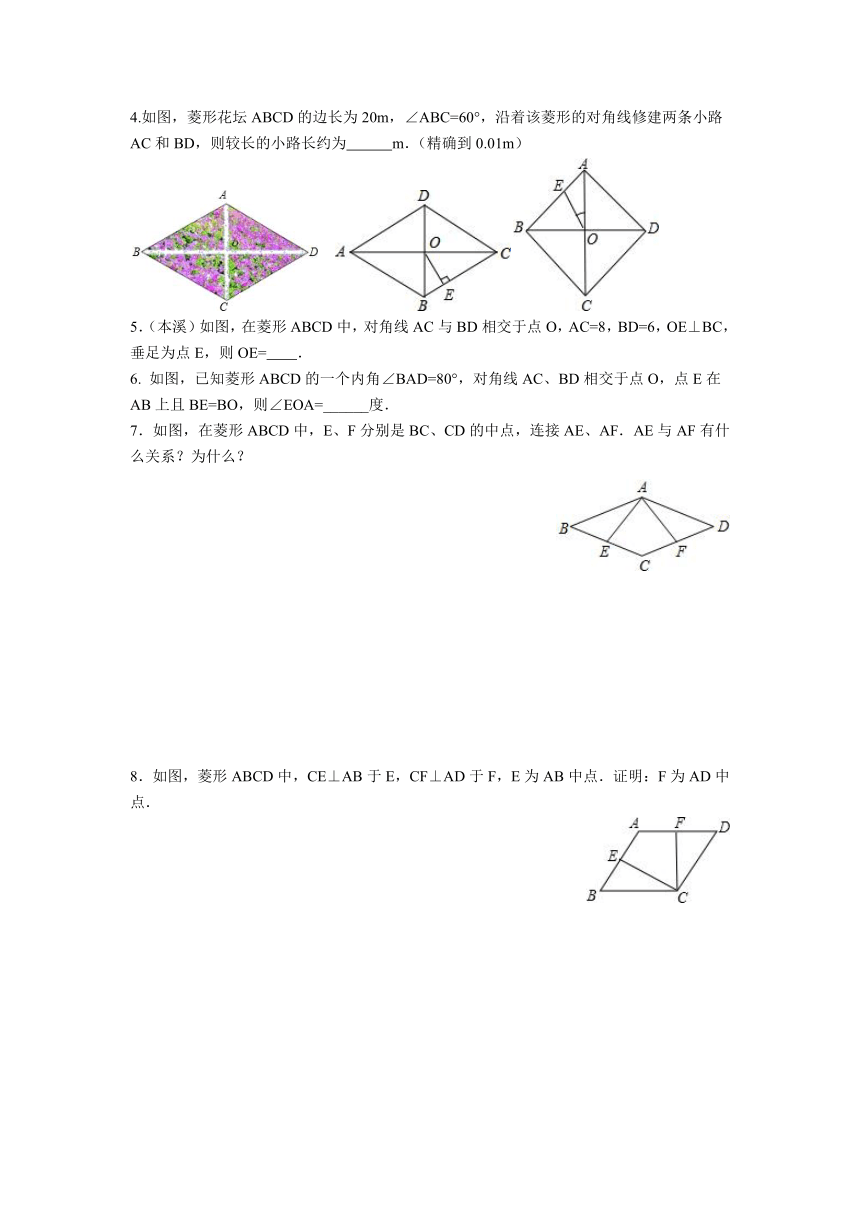
4.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着该菱形的对角线修建两条小路AC和BD,则较长的小路长约为 m.(精确到0.01m)
5.(本溪)如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE= .
6. 如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上且BE=BO,则∠EOA=______度.
7.如图,在菱形ABCD中,E、F分别是BC、CD的中点,连接AE、AF.AE与AF有什么关系?为什么?
8.如图,菱形ABCD中,CE⊥AB于E,CF⊥AD于F,E为AB中点.证明:F为AD中点.
能力提升
9.(吉林)如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为 .
10.如图所示,在边长为2的菱形ABCD中,∠DAB=60°,点E为AB中点,点F是AC上一动点,则EF+BF的最小值为 .(提示:根据轴对称的性质)
第1课时 菱形的性质
自 主 预 习
1. 邻边相等
2.对角线所在的直线;两条对角线的交点
3.相等;互相垂直
4.(1)平行四边形的邻边不一定相等,菱形的每组邻边都相等;
(2)平行四边形不一定是菱形,但菱形一定是平行四边形
(3)菱形具有平行四边形的一切性质。
5.分析:由在菱形ABCD中,BD=6,AC=8,可得OA=AC=4,OB=BD=3,AC⊥BD,然后由勾股定理求得AB的长,继而求得答案.
解:在菱形ABCD中,BD=6,AC=8,
∴OA=AC=4,OB=BD=3,AC⊥BD,
∴AB==5,
∴菱形的周长为:4×5=20.
随 堂 学 练
1.C.
解析:∵菱形的各边长相等,∴边长为3cm的菱形的周长是:3×4=12(cm).
2.B.
解析:∵四边形ABCD是菱形,AC是对角线,∴AB=BC=CD=AD,∠BAC=∠CAD=∠BAD,∴∠BAC=60°,∴△ABC是等边三角形,∵△ABC的周长是15,∴AB=BC=5,∴菱形ABCD的周长是20.
3.D.
解析:∵四边形ABCD是菱形,AC=8,BD=6,∴OB=OD=3,OA=OC=4,AC⊥BD,在Rt△AOB中,
由勾股定理得:AB===5,即菱形ABCD的边长AB=BC=CD=AD=5.
4.D.
解析:根据菱形的对角线互相垂直平分可得:①正确;②错误;根据菱形的对角线平分一组内角可得③正确.④错误.
5. D.
解析:∵菱形的两邻角度数的比是1:5,∴较大的内角为180°×=150°.
6.D.
解析:选项A不正确,两组对边分别平行;选项B不正确,两组对角分别相等,两者均有此性质正确;选项C不正确,对角线互相平分,两者均具有此性质;选项D菱形的对角线互相垂直但平行四边形却无此性质.
7.5.
解析:∵四边形ABCD是菱形,∴AB=BC=CD=AD,∵菱形ABCD的周长为20cm,∴边长为:20÷4=5(cm).
8.6.
解析:∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∴AC=AB=6.
9.35°.
解析:∵四边形ABCD是菱形,∴AC⊥BD,∴∠BOC=90°,∵∠BCO=55°,∴∠CBO=90°﹣55°=35°,∵四边形ABCD是菱形,∴AD∥BC,∴∠ADO=∠CBO=35°,
10.分析:根据中垂线的性质可得AC=DC,又有菱形的性质即可推出△ABC为等边三角形.
证明:∵CE垂直平分AD,
∴AC=DC.
∵四边形ABCD是菱形,
∴AB=BC=DC.
∴AB=BC=AC.
∴△ABC为等边三角形.
课 后 作 业
1.A.
解析:菱形的周长为40cm,则菱形的边长为10cm,菱形的对角线互相垂直,所以△ABO为直角三角形,设菱形的对角线长为2x、2y,则x:y=3:4,在Rt△ABO中,x2+y2=102,解得x=6cm,y=8cm,
故对角线长为12cm,16cm.
2.A.
解析:连接AC交BD于点E,则∠ABE=60°,根据菱形的周长求出AB的长度等于4,在△ABD中,求出BD,继而可得出BE的长.在Rt△ABE中,求出AE=2,故可得AC=2AE=4.
3. C.
解析:∵AD∥BC,∴∠AEB=∠DAE=∠B=80°,∴AE=AB=AD,在三角形AED中,AE=AD,∠DAE=80°,∴∠ADE=50°,又∵∠B=80°,∴∠ADC=80°,∴∠CDE=∠ADC﹣∠ADE=30°.
4. 34.64.
解析:由题意可得,∠ABO=30°,∴OC=10cm,∴OB==10,∴BD=20≈34.64.
5. .
解析:∵四边形ABCD为菱形,∴AC⊥BD,OB=OD=BD=3,OA=OC=AC=4,在Rt△OBC中,∵OB=3,OC=4,∴BC==5,∵OE⊥BC,∴OE BC=OB OC,∴OE==.
6.(,0).
解析:∵菱形周长为12,∴菱形边长AB=12÷4=3,∵∠ABC=120°,∴∠ABO=×120°=60°,∴由勾股定理可求得OA= =,∴点A的坐标为(,0).
7.解:AE=AF
理由:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠B=∠D,
∴BC=CD.
∵E、F分别是BC、CD的中点,
∴BE=BC,DF=CD,
∴BE=DF.
在△ABE和△ADF中
∴△ABE≌△ADF(SAS),
∴AE=AF.
8.分析:连接AC,根据CE⊥AB,且E为AB的中点,即可求证AC=BC,即可证明AC=CD,根据CF⊥AD即可证明F为AD的中点.
证明:连接AC,
∵CE⊥AB,且E为AB的中点
∴△ACB为等腰三角形,即AC=BC,
∵BC=CD,
∴AC=CD,
∵CF⊥AD,
∴F为AD的中点.
9. (4,4).
解析:连接AC、BD交于点E,如图所示:∵四边形ABCD是菱形,∴AC⊥BD,AE=CE=AC,BE=DE=BD,∵点B的坐标为(8,2),点D的坐标为(0,2),∴OD=2,BD=8,∴AE=OD=2,DE=4,
∴AC=4,∴点C的坐标为:(4,4);
10.
解析:首先连接DB,DE,设DE交AC于M,连接MB,DF.证明只有点F运动到点M时,EF+BF取最小值,再根据菱形的性质、勾股定理求得最小值.
∵四边形ABCD是菱形,∴AC,BD互相垂直平分,∴点B关于AC的对称点为D,∴FD=FB,
∴FE+FB=FE+FD≥DE.只有当点F运动到点M时,取等号(两点之间线段最短),△ABD中,AD=AB,∠DAB=60°,∴△ABD是等边三角形.∵E为AB的中点,∴DE⊥AB,∴AE=AD=1,DE===,∴EF+BF的最小值为.
第1课时 菱形的性质
自 主 预 习
1.有一组 的平行四边形叫做菱形.
2.菱形既是轴对称图形,也是中心对称图形,其对称轴是 ,对称中心为 ;
3.菱形的四条边都 ;菱形的对角线 .
4.(想一想)菱形与平行四边形的对应元素之间有什么联系和区别?
5.(做一做)如图,在菱形ABCD中,BD=6,AC=8,求菱形的周长.
随 堂 学 练
知识通关
知识点1 菱形的概念及菱形的性质(边)
1.如图,菱形ABCD中,BE⊥AD,BF⊥CD,F、F为垂足,AE=ED,则∠EBF等于()
A.75° B.60° C.50° D.45°
2.如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是( )
A.25 B.20 C.15 D.10
知识点2菱形的性质(对角线)
3. 如图所示,菱形ABCD在平面直角坐标系中,∠ABC=60°,点A的坐标为(0,),则B、C、D三点的坐标为_______.
4.(昆明)如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论:①AC⊥BD;②OA=OB;③∠ADB=∠CDB;④△ABC是等边三角形,其中一定成立的是( )
A.①② B.③④ C.②③ D.①③
课堂达标
5.已知菱形的两邻角度数的比是1:5,则其中较大的内角是( )
A.60° B.90° C.120° D.150°
6.(泸州)菱形具有而平行四边形不具有的性质是( )
A.两组对边分别平行 B.两组对角分别相等
C.对角线互相平分 D.对角线互相垂直
7.若菱形的周长为20cm,则它的边长是 cm.
8.(东莞)如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长是 .
9.如图,菱形ABCD中,AC、BD相交于点O,若∠BCO=55°,则∠ADO= .
10. 如图所示,四边形ABCD是菱形,直线CE垂直平分AD于点E,连接AC.
求证:△ABC为等边三角形.
课 后 作 业
基础巩固
1.已知菱形的周长等于40cm,两对角线的比为3:4,则对角线的长分别是( )
A.12cm,16cm B.6cm,8cm C.3cm,4cm D.24cm,32cm
2.(龙岩)如图,菱形ABCD的周长为16,∠ABC=120°,则AC的长为( )
A.4 B.4 C.2 D.2
3.如图,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( )
A.20° B.25° C.30° D.35°
4.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着该菱形的对角线修建两条小路AC和BD,则较长的小路长约为 m.(精确到0.01m)
5.(本溪)如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE= .
6. 如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上且BE=BO,则∠EOA=______度.
7.如图,在菱形ABCD中,E、F分别是BC、CD的中点,连接AE、AF.AE与AF有什么关系?为什么?
8.如图,菱形ABCD中,CE⊥AB于E,CF⊥AD于F,E为AB中点.证明:F为AD中点.
能力提升
9.(吉林)如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为 .
10.如图所示,在边长为2的菱形ABCD中,∠DAB=60°,点E为AB中点,点F是AC上一动点,则EF+BF的最小值为 .(提示:根据轴对称的性质)
第1课时 菱形的性质
自 主 预 习
1. 邻边相等
2.对角线所在的直线;两条对角线的交点
3.相等;互相垂直
4.(1)平行四边形的邻边不一定相等,菱形的每组邻边都相等;
(2)平行四边形不一定是菱形,但菱形一定是平行四边形
(3)菱形具有平行四边形的一切性质。
5.分析:由在菱形ABCD中,BD=6,AC=8,可得OA=AC=4,OB=BD=3,AC⊥BD,然后由勾股定理求得AB的长,继而求得答案.
解:在菱形ABCD中,BD=6,AC=8,
∴OA=AC=4,OB=BD=3,AC⊥BD,
∴AB==5,
∴菱形的周长为:4×5=20.
随 堂 学 练
1.C.
解析:∵菱形的各边长相等,∴边长为3cm的菱形的周长是:3×4=12(cm).
2.B.
解析:∵四边形ABCD是菱形,AC是对角线,∴AB=BC=CD=AD,∠BAC=∠CAD=∠BAD,∴∠BAC=60°,∴△ABC是等边三角形,∵△ABC的周长是15,∴AB=BC=5,∴菱形ABCD的周长是20.
3.D.
解析:∵四边形ABCD是菱形,AC=8,BD=6,∴OB=OD=3,OA=OC=4,AC⊥BD,在Rt△AOB中,
由勾股定理得:AB===5,即菱形ABCD的边长AB=BC=CD=AD=5.
4.D.
解析:根据菱形的对角线互相垂直平分可得:①正确;②错误;根据菱形的对角线平分一组内角可得③正确.④错误.
5. D.
解析:∵菱形的两邻角度数的比是1:5,∴较大的内角为180°×=150°.
6.D.
解析:选项A不正确,两组对边分别平行;选项B不正确,两组对角分别相等,两者均有此性质正确;选项C不正确,对角线互相平分,两者均具有此性质;选项D菱形的对角线互相垂直但平行四边形却无此性质.
7.5.
解析:∵四边形ABCD是菱形,∴AB=BC=CD=AD,∵菱形ABCD的周长为20cm,∴边长为:20÷4=5(cm).
8.6.
解析:∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∴AC=AB=6.
9.35°.
解析:∵四边形ABCD是菱形,∴AC⊥BD,∴∠BOC=90°,∵∠BCO=55°,∴∠CBO=90°﹣55°=35°,∵四边形ABCD是菱形,∴AD∥BC,∴∠ADO=∠CBO=35°,
10.分析:根据中垂线的性质可得AC=DC,又有菱形的性质即可推出△ABC为等边三角形.
证明:∵CE垂直平分AD,
∴AC=DC.
∵四边形ABCD是菱形,
∴AB=BC=DC.
∴AB=BC=AC.
∴△ABC为等边三角形.
课 后 作 业
1.A.
解析:菱形的周长为40cm,则菱形的边长为10cm,菱形的对角线互相垂直,所以△ABO为直角三角形,设菱形的对角线长为2x、2y,则x:y=3:4,在Rt△ABO中,x2+y2=102,解得x=6cm,y=8cm,
故对角线长为12cm,16cm.
2.A.
解析:连接AC交BD于点E,则∠ABE=60°,根据菱形的周长求出AB的长度等于4,在△ABD中,求出BD,继而可得出BE的长.在Rt△ABE中,求出AE=2,故可得AC=2AE=4.
3. C.
解析:∵AD∥BC,∴∠AEB=∠DAE=∠B=80°,∴AE=AB=AD,在三角形AED中,AE=AD,∠DAE=80°,∴∠ADE=50°,又∵∠B=80°,∴∠ADC=80°,∴∠CDE=∠ADC﹣∠ADE=30°.
4. 34.64.
解析:由题意可得,∠ABO=30°,∴OC=10cm,∴OB==10,∴BD=20≈34.64.
5. .
解析:∵四边形ABCD为菱形,∴AC⊥BD,OB=OD=BD=3,OA=OC=AC=4,在Rt△OBC中,∵OB=3,OC=4,∴BC==5,∵OE⊥BC,∴OE BC=OB OC,∴OE==.
6.(,0).
解析:∵菱形周长为12,∴菱形边长AB=12÷4=3,∵∠ABC=120°,∴∠ABO=×120°=60°,∴由勾股定理可求得OA= =,∴点A的坐标为(,0).
7.解:AE=AF
理由:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠B=∠D,
∴BC=CD.
∵E、F分别是BC、CD的中点,
∴BE=BC,DF=CD,
∴BE=DF.
在△ABE和△ADF中
∴△ABE≌△ADF(SAS),
∴AE=AF.
8.分析:连接AC,根据CE⊥AB,且E为AB的中点,即可求证AC=BC,即可证明AC=CD,根据CF⊥AD即可证明F为AD的中点.
证明:连接AC,
∵CE⊥AB,且E为AB的中点
∴△ACB为等腰三角形,即AC=BC,
∵BC=CD,
∴AC=CD,
∵CF⊥AD,
∴F为AD的中点.
9. (4,4).
解析:连接AC、BD交于点E,如图所示:∵四边形ABCD是菱形,∴AC⊥BD,AE=CE=AC,BE=DE=BD,∵点B的坐标为(8,2),点D的坐标为(0,2),∴OD=2,BD=8,∴AE=OD=2,DE=4,
∴AC=4,∴点C的坐标为:(4,4);
10.
解析:首先连接DB,DE,设DE交AC于M,连接MB,DF.证明只有点F运动到点M时,EF+BF取最小值,再根据菱形的性质、勾股定理求得最小值.
∵四边形ABCD是菱形,∴AC,BD互相垂直平分,∴点B关于AC的对称点为D,∴FD=FB,
∴FE+FB=FE+FD≥DE.只有当点F运动到点M时,取等号(两点之间线段最短),△ABD中,AD=AB,∠DAB=60°,∴△ABD是等边三角形.∵E为AB的中点,∴DE⊥AB,∴AE=AD=1,DE===,∴EF+BF的最小值为.
