北师大版七下数学3.3用图像表示变量间的关系 课件(23张ppt)
文档属性
| 名称 | 北师大版七下数学3.3用图像表示变量间的关系 课件(23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 08:33:32 | ||
图片预览





文档简介
(共23张PPT)
用图像表示的变量间关系
第三章 第3节
时间/时
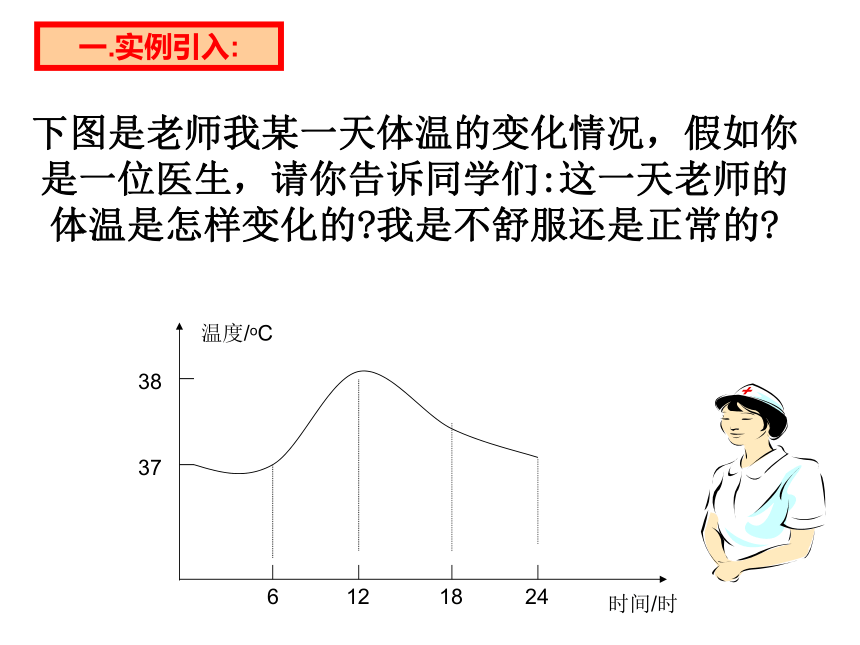
下图是老师我某一天体温的变化情况,假如你是一位医生,请你告诉同学们:这一天老师的体温是怎样变化的 我是不舒服还是正常的
6
12
18
24
37
38
温度/oC
一.实例引入:
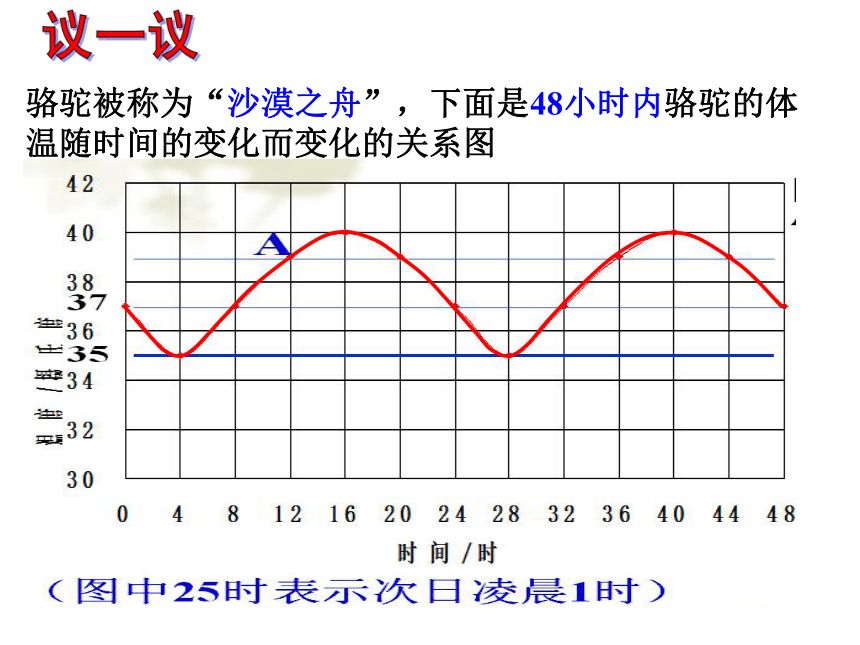
议一议
骆驼被称为“沙漠之舟”,下面是48小时内骆驼的体温随时间的变化而变化的关系图
(图中25时表示次日凌晨1时)
A
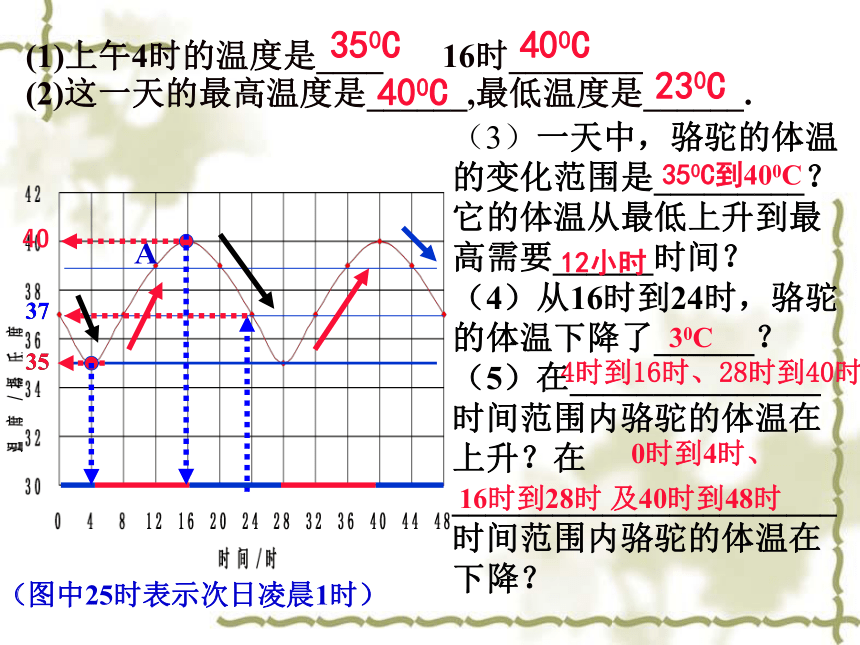
(3)一天中,骆驼的体温的变化范围是_________?它的体温从最低上升到最高需要______时间?
(4)从16时到24时,骆驼的体温下降了______?
(5)在_______________时间范围内骆驼的体温在上升?在_______________________时间范围内骆驼的体温在下降?
37
35
350C到400C
12小时
30C
4时到16时、28时到40时
0时到4时、
16时到28时 及40时到48时
35
40
37
(1)上午4时的温度是____ 16时________
(2)这一天的最高温度是______,最低温度是______.
350C
400C
400C
230C
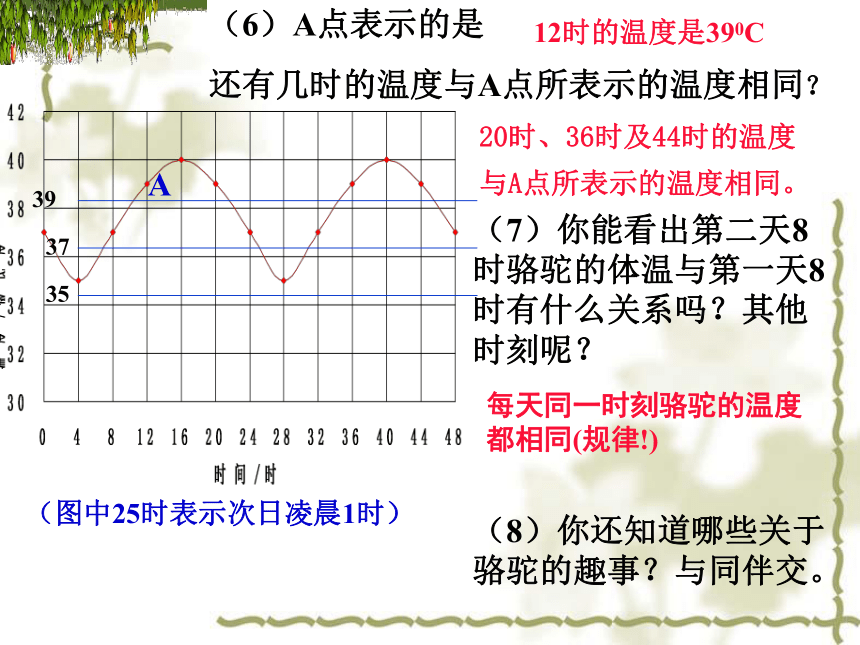
(7)你能看出第二天8时骆驼的体温与第一天8时有什么关系吗?其他时刻呢?
(8)你还知道哪些关于骆驼的趣事?与同伴交。
(图中25时表示次日凌晨1时)
A
35
37
39
每天同一时刻骆驼的温度都相同(规律!)
12时的温度是390C
20时、36时及44时的温度
与A点所表示的温度相同。
(6)A点表示的是
还有几时的温度与A点所表示的温度相同?
骆 驼 趣 事
骆驼非常适合,或者说适应在昼热夜寒、缺少水和绿色植物地上生活,例如非洲的撒哈 拉大沙漠或中亚的戈壁滩。
骆驼吃各种植物,甚至包括其他动物碰都不碰的荆棘和含盐的灌木,为寻找食物,它们会长途跋渺。骆驼具有惊人的能力,可以在缺水的情况下行走很长的时间。
骆驼在它们的身体组织内贮存水,一只骆驼在不工作时可以10个月不喝水。但到了那时,总会变得又瘦又憔悴,如果找到了水,它可以在10分钟内喝下135升。那时,它的身体会膨胀起来,又恢复到正常状态。
骆驼有两种:单峰骆驼(大部分分布在非洲和阿拉伯)只有一个驼峰,而双峰骆驼(来自戈壁沙漠)有两个驼峰。驼峰里贮藏着能量丰富的脂肪。在没有食物又必须行走的情况下,它们就利用这些脂肪来提供能量。
骆驼的睫毛很长,可以挡住风沙。它的皮很厚,夜里可以保暖,白天则隔热。生活在沙漠里的人们将单峰驼用作坐骑。图片显示的是双峰驼,比单峰驼强壮,更适于运输货物。
几千年来,骆驼对于住在亚非沙漠地带人们的生活至关重要。它们不仅运送人和货物,而且还被用作结婚的馈赠礼物,或是杀伤人后的罚金。骆驼也被进口到澳大利亚,其中一些逃到中部沙漠地带,成为野生群落。
海水受日月的引力而产生潮汐现象,早晨海水上涨叫做潮,黄昏海水上涨叫做汐,合称潮汐。潮汐与人类的生活有着密切的联系。下面探讨某港口从0时到12时的水深情况。
说一说
0
1
2
3
4
5
6
7
8
0
1
2
3
4
5
6
7
8
9
10
11
12
时间/时
水深/米
A
B
(1)大约什么时刻港口的水最深?深度约是多少?
(2)大约什么时刻港口的水最浅?深度约是多少?
(3)在什么时间范围内,港口水深在增加?
(4) 在什么时间范围内,港口水深在减少?
(5) A,B两点分别表示什么?还有几时水的深 度与 A点所表示的深度相同?
(6)说一说这个港口从0时到12时的水深是怎样变化的。
看图形回答下面问题
横轴
纵轴
用竖直方向的数轴(称为纵轴)上的点表示因变量。
图象是我们表示变量之间关系的第三种方法,它的特点是非常直观。
在用图象表示变量之间的关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,
变量之间的关系的表示法:(1)表格法 (2)关系式法 (3)图象法
1、某山区今年6月中旬的天气情况是:前5天小雨,后5天暴雨,那么反映该地区某河流水位变化的图像大致是
A
B
C
D
练一练
2、 在夏天一杯开水放在桌面上,其水温T与放置时间 t 的关系大致图象为( )
o
T
t
o
T
t
t
o
T
t
o
T
A
B
C
D
A
3、小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是
.
.
.
A
B
.
C
D
4、小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华的爷爷离公园的距离y与时间x的关系的大致图象是 ( )
.
.
.
B
C
D
x
y
y
y
y
x
x
x
A
5、一个长20厘米的蜡烛,以每小时5厘米的速度燃烧,下面能反映蜡烛剩余的长度与时间关系的图像是( )
6、一个长20厘米的蜡烛,以每小时5厘米的速度燃烧,下面能反映蜡烛燃烧的长度与时间关系的图像是( )
新成药业集团研究开发了一种新药,在实验药效时发现,如果儿童按规定剂量服用,那么2小时的时候血液中含药量最高,接着逐步衰减,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示.当儿童按规定剂量服药后:
(1)何时血液中含药量最高?是多少微克?
(2)A点表示什么意义?
(3)每毫升血液中含药量为2微克以上时
在治疗疾病时是有效的,
那么这个有效期是多长?
联系拓广
图象法中,要深刻理解图象中(1)横轴上的点表示自变 量(2)纵轴上的点表示因变量
小结提高
某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2千米,4小时后,沙尘暴开始经过开阔荒漠地,风速变为平均每小时增加4千米,一段时间,风速保持不变.当沙尘暴经过绿色植被区时,其风速每小时平均减少1千米,最终停止.结合风速和时间的图象,回答下列问题:(1)在纵轴( )内填入相应的数值;
(2)沙尘暴从发生到结束,共经过了多少小时?
1、王大爷带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价出售一些后,又降价出售,售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示。根据图像回答下列问题:
(1)王大爷自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将
剩余土豆售完,这时他手中的钱
(含备用零钱)是26元,
问他一共带了多少千克土豆?
家庭作业
2、水池有2个进水口,1个出水口,每个进水口进水量与时间的关系如下图(1)所示,出水口出水量与时间的关系如图(2)所示,某天0点到6点(至少打开一个水管),该水池的蓄水量与时间的关系如图(3)所示,并给出以下三个论断:a)0点到1点不进水只出水;b)1点到4点不进水,不出水;c)4点到6点只进水,不出水,则一定正确的论断是:
A.a),c) B.b),c) C.c) D.a),b),c)
用图像表示的变量间关系
第三章 第3节
时间/时
下图是老师我某一天体温的变化情况,假如你是一位医生,请你告诉同学们:这一天老师的体温是怎样变化的 我是不舒服还是正常的
6
12
18
24
37
38
温度/oC
一.实例引入:
议一议
骆驼被称为“沙漠之舟”,下面是48小时内骆驼的体温随时间的变化而变化的关系图
(图中25时表示次日凌晨1时)
A
(3)一天中,骆驼的体温的变化范围是_________?它的体温从最低上升到最高需要______时间?
(4)从16时到24时,骆驼的体温下降了______?
(5)在_______________时间范围内骆驼的体温在上升?在_______________________时间范围内骆驼的体温在下降?
37
35
350C到400C
12小时
30C
4时到16时、28时到40时
0时到4时、
16时到28时 及40时到48时
35
40
37
(1)上午4时的温度是____ 16时________
(2)这一天的最高温度是______,最低温度是______.
350C
400C
400C
230C
(7)你能看出第二天8时骆驼的体温与第一天8时有什么关系吗?其他时刻呢?
(8)你还知道哪些关于骆驼的趣事?与同伴交。
(图中25时表示次日凌晨1时)
A
35
37
39
每天同一时刻骆驼的温度都相同(规律!)
12时的温度是390C
20时、36时及44时的温度
与A点所表示的温度相同。
(6)A点表示的是
还有几时的温度与A点所表示的温度相同?
骆 驼 趣 事
骆驼非常适合,或者说适应在昼热夜寒、缺少水和绿色植物地上生活,例如非洲的撒哈 拉大沙漠或中亚的戈壁滩。
骆驼吃各种植物,甚至包括其他动物碰都不碰的荆棘和含盐的灌木,为寻找食物,它们会长途跋渺。骆驼具有惊人的能力,可以在缺水的情况下行走很长的时间。
骆驼在它们的身体组织内贮存水,一只骆驼在不工作时可以10个月不喝水。但到了那时,总会变得又瘦又憔悴,如果找到了水,它可以在10分钟内喝下135升。那时,它的身体会膨胀起来,又恢复到正常状态。
骆驼有两种:单峰骆驼(大部分分布在非洲和阿拉伯)只有一个驼峰,而双峰骆驼(来自戈壁沙漠)有两个驼峰。驼峰里贮藏着能量丰富的脂肪。在没有食物又必须行走的情况下,它们就利用这些脂肪来提供能量。
骆驼的睫毛很长,可以挡住风沙。它的皮很厚,夜里可以保暖,白天则隔热。生活在沙漠里的人们将单峰驼用作坐骑。图片显示的是双峰驼,比单峰驼强壮,更适于运输货物。
几千年来,骆驼对于住在亚非沙漠地带人们的生活至关重要。它们不仅运送人和货物,而且还被用作结婚的馈赠礼物,或是杀伤人后的罚金。骆驼也被进口到澳大利亚,其中一些逃到中部沙漠地带,成为野生群落。
海水受日月的引力而产生潮汐现象,早晨海水上涨叫做潮,黄昏海水上涨叫做汐,合称潮汐。潮汐与人类的生活有着密切的联系。下面探讨某港口从0时到12时的水深情况。
说一说
0
1
2
3
4
5
6
7
8
0
1
2
3
4
5
6
7
8
9
10
11
12
时间/时
水深/米
A
B
(1)大约什么时刻港口的水最深?深度约是多少?
(2)大约什么时刻港口的水最浅?深度约是多少?
(3)在什么时间范围内,港口水深在增加?
(4) 在什么时间范围内,港口水深在减少?
(5) A,B两点分别表示什么?还有几时水的深 度与 A点所表示的深度相同?
(6)说一说这个港口从0时到12时的水深是怎样变化的。
看图形回答下面问题
横轴
纵轴
用竖直方向的数轴(称为纵轴)上的点表示因变量。
图象是我们表示变量之间关系的第三种方法,它的特点是非常直观。
在用图象表示变量之间的关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,
变量之间的关系的表示法:(1)表格法 (2)关系式法 (3)图象法
1、某山区今年6月中旬的天气情况是:前5天小雨,后5天暴雨,那么反映该地区某河流水位变化的图像大致是
A
B
C
D
练一练
2、 在夏天一杯开水放在桌面上,其水温T与放置时间 t 的关系大致图象为( )
o
T
t
o
T
t
t
o
T
t
o
T
A
B
C
D
A
3、小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是
.
.
.
A
B
.
C
D
4、小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华的爷爷离公园的距离y与时间x的关系的大致图象是 ( )
.
.
.
B
C
D
x
y
y
y
y
x
x
x
A
5、一个长20厘米的蜡烛,以每小时5厘米的速度燃烧,下面能反映蜡烛剩余的长度与时间关系的图像是( )
6、一个长20厘米的蜡烛,以每小时5厘米的速度燃烧,下面能反映蜡烛燃烧的长度与时间关系的图像是( )
新成药业集团研究开发了一种新药,在实验药效时发现,如果儿童按规定剂量服用,那么2小时的时候血液中含药量最高,接着逐步衰减,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示.当儿童按规定剂量服药后:
(1)何时血液中含药量最高?是多少微克?
(2)A点表示什么意义?
(3)每毫升血液中含药量为2微克以上时
在治疗疾病时是有效的,
那么这个有效期是多长?
联系拓广
图象法中,要深刻理解图象中(1)横轴上的点表示自变 量(2)纵轴上的点表示因变量
小结提高
某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2千米,4小时后,沙尘暴开始经过开阔荒漠地,风速变为平均每小时增加4千米,一段时间,风速保持不变.当沙尘暴经过绿色植被区时,其风速每小时平均减少1千米,最终停止.结合风速和时间的图象,回答下列问题:(1)在纵轴( )内填入相应的数值;
(2)沙尘暴从发生到结束,共经过了多少小时?
1、王大爷带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价出售一些后,又降价出售,售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示。根据图像回答下列问题:
(1)王大爷自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将
剩余土豆售完,这时他手中的钱
(含备用零钱)是26元,
问他一共带了多少千克土豆?
家庭作业
2、水池有2个进水口,1个出水口,每个进水口进水量与时间的关系如下图(1)所示,出水口出水量与时间的关系如图(2)所示,某天0点到6点(至少打开一个水管),该水池的蓄水量与时间的关系如图(3)所示,并给出以下三个论断:a)0点到1点不进水只出水;b)1点到4点不进水,不出水;c)4点到6点只进水,不出水,则一定正确的论断是:
A.a),c) B.b),c) C.c) D.a),b),c)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
