北师大版五年级下册数学第七单元测试卷(含答案)
文档属性
| 名称 | 北师大版五年级下册数学第七单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 72.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 21:02:48 | ||
图片预览




文档简介
第七单元测试卷(含答案)
学校:___________姓名:___________班级:___________考号:___________
一、填空题(共41分)
1.(本题3分)在学校组织的才艺展示活动中,书法组有28人,比舞蹈组人数的2倍多6人,舞蹈组有( )人。
2.(本题3分)妈妈带200元去商店买了6盒礼品,每盒礼品x元,还剩30元.根据题意列出的方程是( )=200.
3.(本题3分)有两堆煤,甲堆94吨,乙堆138吨,每天各运走9吨,经过____天后乙堆剩下的煤是甲堆剩下的3倍。
4.(本题6分)写出下面式子所表示的意义。
徒弟每小时加工a个零件,师傅每小时加工的零件数是徒弟的2倍。
2a表示:_________
2a-a表示:_________
2a+a表示:_________
5.(本题8分)在括号里填上合适的数,使每个方程的解都是。
( )+=8 ( )-=24
×( )=2.4 ÷( )=400%
6.(本题6分)商店卖出面粉2000克,卖出去的大米是面粉的4倍,卖出大米( )克,面粉和大米一共卖出( )千克。
7.(本题3分)学校开展课外阅读活动,兰兰读一本《国学经典》,原计划每天读25页,实际每天多读10页,结果比原来提前了6天读完。这本《国学经典》共有________页。
8.(本题3分)小红有两盒糖果盒,糖果盒的尺寸大小如图,现在小红打算把这两盒糖果盒进行包装,不考虑接口处,最少需要( )dm2的包装纸。
9.(本题6分)找出数量间的等量关系,再把每个方程补充完整。
小华拿8元钱去买作业本,每本作业0.75元,买了本后,找回3.5元。
等量关系:( )
方程:( )=3.5
二、选择题(共12分)
10.(本题2分)五个连续的自然数,如果第二个数用m表示,那么第五个数是( )。
A.m+2 B.m+3 C.m+4 D.m+5
11.(本题2分)在下面的方程中,与方程2x=6的解相同的是( )
A.x÷3=1 B.4.2-x=1.5 C.0.5x+0.3=4.5 D.4x=16
12.(本题2分)今年爸爸和方媛的年龄和是43岁,爸爸的年龄比方媛年龄的4倍多3岁,今年方媛多少岁?如果设今年方媛x岁,列式为( )。
A.4x+3=43 B.4x+3+x=43 C.4x-3=43 D.4x-3+x=43
13.(本题2分)甲袋面粉有千克,乙袋面粉有千克.若从甲袋中倒出5千克放入乙袋,则两袋面粉一样重.下面等式中不符合题意的是( ).A. B. C. D.
14.(本题2分)一个书架有上下两层,上层放书的本数是下层的3倍。如果把新买的78本书放入下层,那么两层书的本数就同样多。原来上下层各有书( )本。(用方程解)
A.上层原有书105本,下层原有书35本 B.上层原有书123本,下层原有书41本
C.上层原有书117本,下层原有书39本 D.上层原有书156本,下层原有书52本
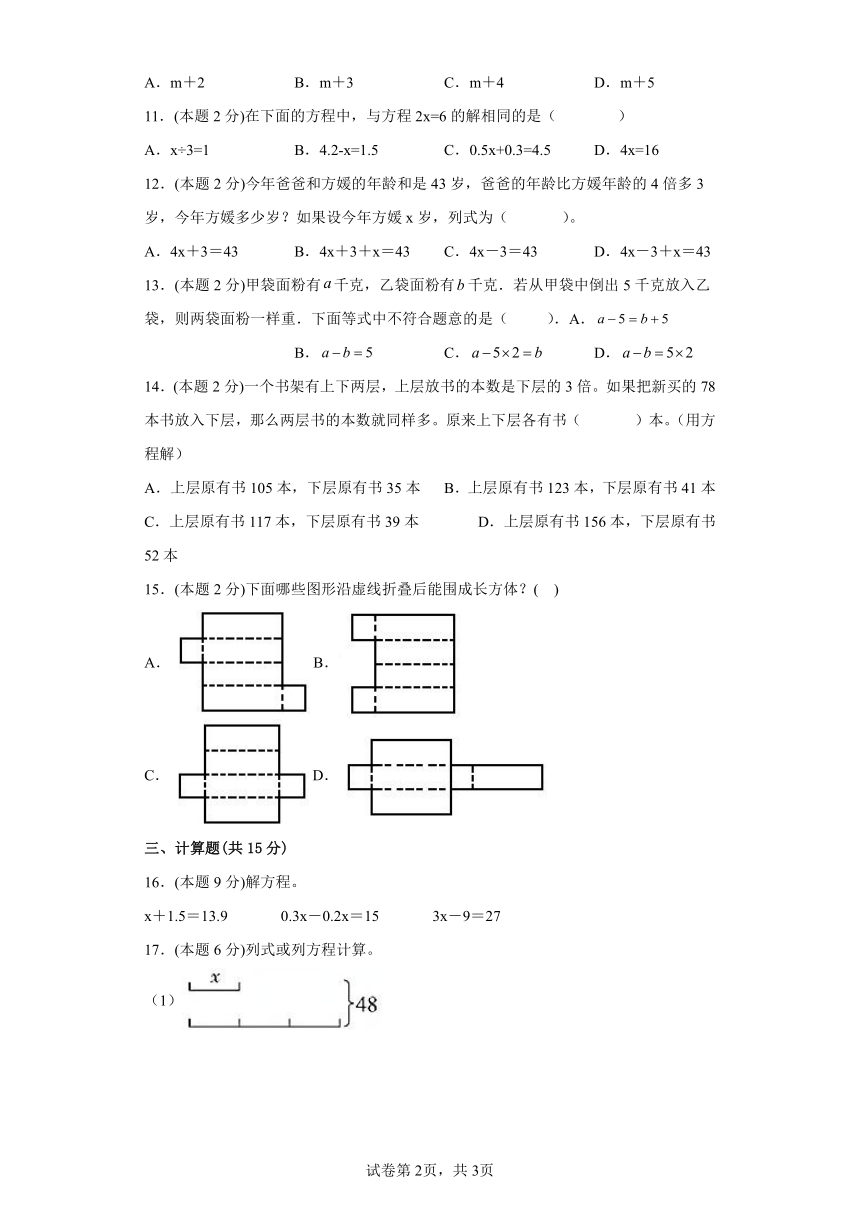
15.(本题2分)下面哪些图形沿虚线折叠后能围成长方体?( )
A.B.
C.D.
三、计算题(共15分)
16.(本题9分)解方程。
x+1.5=13.9 0.3x-0.2x=15 3x-9=27
17.(本题6分)列式或列方程计算。
(1)
(2)
四、解答题(共32分)
18.(本题5分)体育老师买了5大盒和5小盒羽毛球,共100只。已知1小盒装的羽毛球比1大盒装少4只,每大盒装多少只羽毛球?
19.(本题5分)甲地到乙地的铁路线长920km。一列火车从甲地出发,每时行120km,另一列火车从乙地开出,每时行110km。两列火车同时出发,经过几时相遇?(列方程解答)
20.(本题5分)一副乒乓球拍的价钱比一副羽毛球拍贵19元。乒乓球拍的价钱是羽毛球拍的1.5倍,一副乒乓球拍和一副羽毛球拍的单价是多少钱?(列方程解答)
21.(本题5分)小明和小华在一个周长为400米的环形跑道上练习跑步,两人同时从同一地点出发,背向而行.小明每秒跑3.5米,小华每秒跑4.5米.经过多少秒两人第一次相遇?
22.(本题6分)甲、乙两个修路队同时合修一条长6.48km的公路,已知甲队平均每天修0.15km,乙队平均每天修0.12km,两个修路队合修这条公路一共需要多少天?
23.(本题6分)有4个棱长是2dm的正方体礼品盒,现在把它们用包装纸包成一包,有两种方案(如图)。哪种方案比较节省包装纸?至少需要多少dm2包装纸?(不计损耗)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.11
【解析】
【分析】
设舞蹈组有x人,舞蹈组的人数×2+6=书法组人数,据此列方程解答。
【详解】
解:设舞蹈组有x人。
2x+6=28
2x=22
x=11
舞蹈组有11人。
【点睛】
此题考查了列方程解决问题,找准等量关系,认真解答即可。
2.6x+30
【解析】
【详解】
略
3.8
【解析】
【分析】
本题用方程解答较容易理解。可设经过天后,乙堆剩下的煤是甲堆剩下的3倍,那么甲堆94吨减天运走后的煤重量的3倍等于乙堆138吨减天运走后的煤重量,据此解答。
【详解】
解:设经过x天后,乙堆剩下的煤是甲堆剩下的3倍。
(94-9x)×3=138-9x
282-27x=138-9x
282-27x+27x=138-9x+27x
282-138=138+18x-138
18x=144
x=8
【点睛】
找出经过天后,甲堆煤的重量和乙堆煤重量之间的等量关系,是解答本题的关键。
4. 师傅每小时加工的零件数 师傅每小时比徒弟每小时多加工的零件数 师傅每小时和徒弟每小时共加工的零件数
【解析】
【分析】
用2乘a求出师傅每小时加工的零件数;用师傅每小时加工的零件数减去a求出师傅每小时比徒弟每小时多加工的零件数;用师傅每小时加工的零件数加上a求出师傅每小时和徒弟每小时共加工的零件数。
【详解】
根据分析可得:2a表示:师傅每小时加工的零件数;2a-a表示:师傅每小时比徒弟每小时多加工的零件数;2a+a表示:师傅每小时和徒弟每小时共加工的零件数。
【点睛】
熟练掌握用字母表示数的知识,是解答此题的关键。
5. 2 30 0.4 1.5
【解析】
【分析】
把代入等式中,把括号看作未知数a,解方程即可。
【详解】
当时,
a+6=8
解:a=8-6
a=2
a-6=24
解:a=24+6
a=30
6×a=2.4
解:a=2.4÷6
a=0.4
6÷a=400%
解:a=6÷4
a=1.5
【点睛】
此题考查的本质是解方程,主要根据等式的性质,等式两边同时加或减相同的数等式仍然成立;等式两边同时乘或除以相同的数(不为0)等式仍然成立。
6. 8000 10
【解析】
【分析】
卖出去的大米是面粉的4倍,2000乘4即可求出卖出大米的质量,再把所得积与2000相加即可求出共卖出大米与面粉的质量,最后把单位化为千克即可。
【详解】
2000×4=8000(克),卖出大米8000克;
2000+8000=10000(克)
10000克=10千克,大米与面粉一共卖出10千克。
【点睛】
1千克=1000克,据此换算单位。
7.525
【解析】
【分析】
用列方程的方法解答比较容易理解。设原来读完需要x天,则现在需要(x-6)天,现在每天读(25+10)页,分别表示出这本书的总页数,然后根据总页数不变列出方程,解方程求出原来读完需要的天数,进而求出总页数即可。
【详解】
解:设原来读完需要x天。
(25+10)×(x-6)=25x
35×(x-6)=25x
35x-35×6=25x
35x-25x=210
10x=210
x=210÷10
x=21
总页数:25×21=525(页)
【点睛】
本题是根据等量关系解答问题,找出相关的量,列方程,解方程。
8.20
【解析】
【分析】
面和面重合,会减少两个面的面积;据此,可尽量使减少的面积最多,使用包装纸的面积就最少;结合具体的长、宽、高数值,可知要使长×宽这个面重合;则进行包装后,新的长不变为2分米、宽不变为1.5分米、高变为原来的2倍,是2分米;再应用长方体表面积公式可计算出最少使用包装纸的面积。
【详解】
1×2=2(dm)
(2×1.5+1.5×2+2×2)×2
=(3+3+4)×2
=10×2
=20(dm2)
【点睛】
首先明确面与面重合会同时减少两个面的面积;再来设计包装纸的长、宽、高,其次计算时,注意将变化后的长、宽、高的数值准确对号入座,不要弄错。
9. 总钱数-每本作业钱数×本数=找回钱数
【解析】
略
10.B
【解析】
【分析】
根据每相邻的两个整数相差是1,第二个数是m,则后面的自然数分别是:m+1, m+2,m+3,据此解答。
【详解】
由分析可知:
那么第五个数是m+3。
故选:B
【点睛】
明确每相邻的两个整数相差是1,是解答此题的关键。
11.A
【解析】
【详解】
略
12.B
【解析】
设今年方媛x岁,那么爸爸的年龄是4x+3岁,根据今年爸爸年龄+方媛年龄=43,列出方程即可。
【详解】
根据分析,列方程为4x+3+x=43。
故答案为:B
【点睛】
本题考查了列方程解决问题,关键是找到等量关系。
13.B
【解析】
【详解】
略
14.C
【解析】
【分析】
根据题意可知,设下层有x本,那么上层有3x本,依据上层的本数=下层的本数+78,据此列方程解答。
【详解】
解:设下层有x本,那么上层有3x本,
3x=x+78
3x-x=78
2x=78
2x÷2=78÷2
x=39
上层:39×3=117(本)。
故答案为:C。
【点睛】
此题考查了列方程解决实际问题,找出等量关系,分别表示出上、下层书的本数是解题关键。
15.A
【解析】
【详解】
把图形围起来之后既没有重合的面,也没有缺面.上面几个图形只有A符合条件.
故答案为A
(1)x=12.4;x=150;x=12
【解析】
【分析】
解方程主要运用等式的性质,等式两边同时加上或者减去同一个数,等式不变。等式两边同时乘或者除以一个不为0的数,等式不变。把含有x的放在等号的一侧,不含x的放在等号的另一侧,然后把x前的系数除过去,就能得出x是多少。
【详解】
x+1.5=13.9
解:x=13.9-1.5
x=12.4
0.3x-0.2x=15
解:0.1x=15
x=15÷0.1
x=150
3x-9=27
解:3x=27+9
3x=36
x=36÷3
x=12
(1)12
(2)17.16元
【解析】
【分析】
较短的线段表示x,则较长的线段表示3x,相加等于48,据此列方程计算。
【详解】
x+3x=48
解:4x=48
x=12
【解析】
【分析】
根据图可知,两本书+一个羽毛球拍=86元,由于一本书的价格是x元,两本书是2x元,一个羽毛球拍的价格是54元,把数代入等式即可列方程,再根据等式的性质解方程即可。
【详解】
2x+54=86
解:2x=86-54
2x=32
x=32÷2
x=16
18.12只
【解析】
【分析】
设每大盒装x只羽毛球,则每小盒装x-4只羽毛球,根据“每大盒羽毛球的个数×大盒的盒数+每小盒羽毛球的只数×小盒的盒数=羽毛球的总只数”可列出方程,求解即可得出答案。
【详解】
解:设每大盒装x只羽毛球,则每小盒装x-4只羽毛球,可得
5x+5×(x-4)=100
5x+5x-20=100
10x=120
x=12
答:每大盒装12只羽毛球。
【点睛】
此题主要考查了列方程解答应用题,要认真分析题意,找出等量关系式是解答的关键。
19.3小时
【解析】
【分析】
根据题意可得等量关系式:速度和×相遇时间=路程,然后设两车x时相遇,然后列方程解答即可。
【详解】
解:设两车x时相遇,
(120+110)x=690
230x=690
x=3
答:两列火车同时出发,经过3小时相遇。
【点睛】
此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
20.羽毛球拍38元;乒乓球拍57元
【解析】
【详解】
解:设一副羽毛球拍的单价是x元,则一副乒乓球拍的单价是1.5x
19+x=1.5x
x=38
38+19=57(元)
21.50秒
【解析】
【详解】
略
22.24天
【解析】
【分析】
两个修路队合修这条公路需要的天数=这条路的总长度÷(甲队平均每天修的长度+乙队平均每天修的长度)。
【详解】
6.48÷(0.15+0.12)
=6.48÷0.27
=24(天)
答:两个修路队合修这条公路一共需要24天。
【点睛】
掌握工作总量、工作效率、工作时间之间的关系是解答题目的关键。
23.A方案;64dm2
【解析】
【分析】
长方体的表面积=(长×宽+长×高+宽×高)×2,A方案中的礼品盒长为2×2dm,宽为2dm,高为2×2dm(长×宽和宽×高相等)即为礼盒表面积=长×宽×4+长×高×2;方案B中的礼品盒长为2×4dm,宽为1dm,高为1dm(长×宽和长×高相等)即礼盒表面积=长×宽×4+宽×高×2;代入数值计算并比较大小即可得出答案。
【详解】
A方案:
(2×2)×(2×2)×2+(2×2)×2×4
=32+32
=64(dm2)
B方案:
(2×4)×2×4+2×2×2
=64+8
=72(dm2)
因为64dm2<72dm2,所以A方案比较节省包装纸。
答:A方案比较节省包装纸。至少需要64dm2包装纸。
【点睛】
考查了长方体表面积的实际应用,计算时要认真。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、填空题(共41分)
1.(本题3分)在学校组织的才艺展示活动中,书法组有28人,比舞蹈组人数的2倍多6人,舞蹈组有( )人。
2.(本题3分)妈妈带200元去商店买了6盒礼品,每盒礼品x元,还剩30元.根据题意列出的方程是( )=200.
3.(本题3分)有两堆煤,甲堆94吨,乙堆138吨,每天各运走9吨,经过____天后乙堆剩下的煤是甲堆剩下的3倍。
4.(本题6分)写出下面式子所表示的意义。
徒弟每小时加工a个零件,师傅每小时加工的零件数是徒弟的2倍。
2a表示:_________
2a-a表示:_________
2a+a表示:_________
5.(本题8分)在括号里填上合适的数,使每个方程的解都是。
( )+=8 ( )-=24
×( )=2.4 ÷( )=400%
6.(本题6分)商店卖出面粉2000克,卖出去的大米是面粉的4倍,卖出大米( )克,面粉和大米一共卖出( )千克。
7.(本题3分)学校开展课外阅读活动,兰兰读一本《国学经典》,原计划每天读25页,实际每天多读10页,结果比原来提前了6天读完。这本《国学经典》共有________页。
8.(本题3分)小红有两盒糖果盒,糖果盒的尺寸大小如图,现在小红打算把这两盒糖果盒进行包装,不考虑接口处,最少需要( )dm2的包装纸。
9.(本题6分)找出数量间的等量关系,再把每个方程补充完整。
小华拿8元钱去买作业本,每本作业0.75元,买了本后,找回3.5元。
等量关系:( )
方程:( )=3.5
二、选择题(共12分)
10.(本题2分)五个连续的自然数,如果第二个数用m表示,那么第五个数是( )。
A.m+2 B.m+3 C.m+4 D.m+5
11.(本题2分)在下面的方程中,与方程2x=6的解相同的是( )
A.x÷3=1 B.4.2-x=1.5 C.0.5x+0.3=4.5 D.4x=16
12.(本题2分)今年爸爸和方媛的年龄和是43岁,爸爸的年龄比方媛年龄的4倍多3岁,今年方媛多少岁?如果设今年方媛x岁,列式为( )。
A.4x+3=43 B.4x+3+x=43 C.4x-3=43 D.4x-3+x=43
13.(本题2分)甲袋面粉有千克,乙袋面粉有千克.若从甲袋中倒出5千克放入乙袋,则两袋面粉一样重.下面等式中不符合题意的是( ).A. B. C. D.
14.(本题2分)一个书架有上下两层,上层放书的本数是下层的3倍。如果把新买的78本书放入下层,那么两层书的本数就同样多。原来上下层各有书( )本。(用方程解)
A.上层原有书105本,下层原有书35本 B.上层原有书123本,下层原有书41本
C.上层原有书117本,下层原有书39本 D.上层原有书156本,下层原有书52本
15.(本题2分)下面哪些图形沿虚线折叠后能围成长方体?( )
A.B.
C.D.
三、计算题(共15分)
16.(本题9分)解方程。
x+1.5=13.9 0.3x-0.2x=15 3x-9=27
17.(本题6分)列式或列方程计算。
(1)
(2)
四、解答题(共32分)
18.(本题5分)体育老师买了5大盒和5小盒羽毛球,共100只。已知1小盒装的羽毛球比1大盒装少4只,每大盒装多少只羽毛球?
19.(本题5分)甲地到乙地的铁路线长920km。一列火车从甲地出发,每时行120km,另一列火车从乙地开出,每时行110km。两列火车同时出发,经过几时相遇?(列方程解答)
20.(本题5分)一副乒乓球拍的价钱比一副羽毛球拍贵19元。乒乓球拍的价钱是羽毛球拍的1.5倍,一副乒乓球拍和一副羽毛球拍的单价是多少钱?(列方程解答)
21.(本题5分)小明和小华在一个周长为400米的环形跑道上练习跑步,两人同时从同一地点出发,背向而行.小明每秒跑3.5米,小华每秒跑4.5米.经过多少秒两人第一次相遇?
22.(本题6分)甲、乙两个修路队同时合修一条长6.48km的公路,已知甲队平均每天修0.15km,乙队平均每天修0.12km,两个修路队合修这条公路一共需要多少天?
23.(本题6分)有4个棱长是2dm的正方体礼品盒,现在把它们用包装纸包成一包,有两种方案(如图)。哪种方案比较节省包装纸?至少需要多少dm2包装纸?(不计损耗)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.11
【解析】
【分析】
设舞蹈组有x人,舞蹈组的人数×2+6=书法组人数,据此列方程解答。
【详解】
解:设舞蹈组有x人。
2x+6=28
2x=22
x=11
舞蹈组有11人。
【点睛】
此题考查了列方程解决问题,找准等量关系,认真解答即可。
2.6x+30
【解析】
【详解】
略
3.8
【解析】
【分析】
本题用方程解答较容易理解。可设经过天后,乙堆剩下的煤是甲堆剩下的3倍,那么甲堆94吨减天运走后的煤重量的3倍等于乙堆138吨减天运走后的煤重量,据此解答。
【详解】
解:设经过x天后,乙堆剩下的煤是甲堆剩下的3倍。
(94-9x)×3=138-9x
282-27x=138-9x
282-27x+27x=138-9x+27x
282-138=138+18x-138
18x=144
x=8
【点睛】
找出经过天后,甲堆煤的重量和乙堆煤重量之间的等量关系,是解答本题的关键。
4. 师傅每小时加工的零件数 师傅每小时比徒弟每小时多加工的零件数 师傅每小时和徒弟每小时共加工的零件数
【解析】
【分析】
用2乘a求出师傅每小时加工的零件数;用师傅每小时加工的零件数减去a求出师傅每小时比徒弟每小时多加工的零件数;用师傅每小时加工的零件数加上a求出师傅每小时和徒弟每小时共加工的零件数。
【详解】
根据分析可得:2a表示:师傅每小时加工的零件数;2a-a表示:师傅每小时比徒弟每小时多加工的零件数;2a+a表示:师傅每小时和徒弟每小时共加工的零件数。
【点睛】
熟练掌握用字母表示数的知识,是解答此题的关键。
5. 2 30 0.4 1.5
【解析】
【分析】
把代入等式中,把括号看作未知数a,解方程即可。
【详解】
当时,
a+6=8
解:a=8-6
a=2
a-6=24
解:a=24+6
a=30
6×a=2.4
解:a=2.4÷6
a=0.4
6÷a=400%
解:a=6÷4
a=1.5
【点睛】
此题考查的本质是解方程,主要根据等式的性质,等式两边同时加或减相同的数等式仍然成立;等式两边同时乘或除以相同的数(不为0)等式仍然成立。
6. 8000 10
【解析】
【分析】
卖出去的大米是面粉的4倍,2000乘4即可求出卖出大米的质量,再把所得积与2000相加即可求出共卖出大米与面粉的质量,最后把单位化为千克即可。
【详解】
2000×4=8000(克),卖出大米8000克;
2000+8000=10000(克)
10000克=10千克,大米与面粉一共卖出10千克。
【点睛】
1千克=1000克,据此换算单位。
7.525
【解析】
【分析】
用列方程的方法解答比较容易理解。设原来读完需要x天,则现在需要(x-6)天,现在每天读(25+10)页,分别表示出这本书的总页数,然后根据总页数不变列出方程,解方程求出原来读完需要的天数,进而求出总页数即可。
【详解】
解:设原来读完需要x天。
(25+10)×(x-6)=25x
35×(x-6)=25x
35x-35×6=25x
35x-25x=210
10x=210
x=210÷10
x=21
总页数:25×21=525(页)
【点睛】
本题是根据等量关系解答问题,找出相关的量,列方程,解方程。
8.20
【解析】
【分析】
面和面重合,会减少两个面的面积;据此,可尽量使减少的面积最多,使用包装纸的面积就最少;结合具体的长、宽、高数值,可知要使长×宽这个面重合;则进行包装后,新的长不变为2分米、宽不变为1.5分米、高变为原来的2倍,是2分米;再应用长方体表面积公式可计算出最少使用包装纸的面积。
【详解】
1×2=2(dm)
(2×1.5+1.5×2+2×2)×2
=(3+3+4)×2
=10×2
=20(dm2)
【点睛】
首先明确面与面重合会同时减少两个面的面积;再来设计包装纸的长、宽、高,其次计算时,注意将变化后的长、宽、高的数值准确对号入座,不要弄错。
9. 总钱数-每本作业钱数×本数=找回钱数
【解析】
略
10.B
【解析】
【分析】
根据每相邻的两个整数相差是1,第二个数是m,则后面的自然数分别是:m+1, m+2,m+3,据此解答。
【详解】
由分析可知:
那么第五个数是m+3。
故选:B
【点睛】
明确每相邻的两个整数相差是1,是解答此题的关键。
11.A
【解析】
【详解】
略
12.B
【解析】
设今年方媛x岁,那么爸爸的年龄是4x+3岁,根据今年爸爸年龄+方媛年龄=43,列出方程即可。
【详解】
根据分析,列方程为4x+3+x=43。
故答案为:B
【点睛】
本题考查了列方程解决问题,关键是找到等量关系。
13.B
【解析】
【详解】
略
14.C
【解析】
【分析】
根据题意可知,设下层有x本,那么上层有3x本,依据上层的本数=下层的本数+78,据此列方程解答。
【详解】
解:设下层有x本,那么上层有3x本,
3x=x+78
3x-x=78
2x=78
2x÷2=78÷2
x=39
上层:39×3=117(本)。
故答案为:C。
【点睛】
此题考查了列方程解决实际问题,找出等量关系,分别表示出上、下层书的本数是解题关键。
15.A
【解析】
【详解】
把图形围起来之后既没有重合的面,也没有缺面.上面几个图形只有A符合条件.
故答案为A
(1)x=12.4;x=150;x=12
【解析】
【分析】
解方程主要运用等式的性质,等式两边同时加上或者减去同一个数,等式不变。等式两边同时乘或者除以一个不为0的数,等式不变。把含有x的放在等号的一侧,不含x的放在等号的另一侧,然后把x前的系数除过去,就能得出x是多少。
【详解】
x+1.5=13.9
解:x=13.9-1.5
x=12.4
0.3x-0.2x=15
解:0.1x=15
x=15÷0.1
x=150
3x-9=27
解:3x=27+9
3x=36
x=36÷3
x=12
(1)12
(2)17.16元
【解析】
【分析】
较短的线段表示x,则较长的线段表示3x,相加等于48,据此列方程计算。
【详解】
x+3x=48
解:4x=48
x=12
【解析】
【分析】
根据图可知,两本书+一个羽毛球拍=86元,由于一本书的价格是x元,两本书是2x元,一个羽毛球拍的价格是54元,把数代入等式即可列方程,再根据等式的性质解方程即可。
【详解】
2x+54=86
解:2x=86-54
2x=32
x=32÷2
x=16
18.12只
【解析】
【分析】
设每大盒装x只羽毛球,则每小盒装x-4只羽毛球,根据“每大盒羽毛球的个数×大盒的盒数+每小盒羽毛球的只数×小盒的盒数=羽毛球的总只数”可列出方程,求解即可得出答案。
【详解】
解:设每大盒装x只羽毛球,则每小盒装x-4只羽毛球,可得
5x+5×(x-4)=100
5x+5x-20=100
10x=120
x=12
答:每大盒装12只羽毛球。
【点睛】
此题主要考查了列方程解答应用题,要认真分析题意,找出等量关系式是解答的关键。
19.3小时
【解析】
【分析】
根据题意可得等量关系式:速度和×相遇时间=路程,然后设两车x时相遇,然后列方程解答即可。
【详解】
解:设两车x时相遇,
(120+110)x=690
230x=690
x=3
答:两列火车同时出发,经过3小时相遇。
【点睛】
此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
20.羽毛球拍38元;乒乓球拍57元
【解析】
【详解】
解:设一副羽毛球拍的单价是x元,则一副乒乓球拍的单价是1.5x
19+x=1.5x
x=38
38+19=57(元)
21.50秒
【解析】
【详解】
略
22.24天
【解析】
【分析】
两个修路队合修这条公路需要的天数=这条路的总长度÷(甲队平均每天修的长度+乙队平均每天修的长度)。
【详解】
6.48÷(0.15+0.12)
=6.48÷0.27
=24(天)
答:两个修路队合修这条公路一共需要24天。
【点睛】
掌握工作总量、工作效率、工作时间之间的关系是解答题目的关键。
23.A方案;64dm2
【解析】
【分析】
长方体的表面积=(长×宽+长×高+宽×高)×2,A方案中的礼品盒长为2×2dm,宽为2dm,高为2×2dm(长×宽和宽×高相等)即为礼盒表面积=长×宽×4+长×高×2;方案B中的礼品盒长为2×4dm,宽为1dm,高为1dm(长×宽和长×高相等)即礼盒表面积=长×宽×4+宽×高×2;代入数值计算并比较大小即可得出答案。
【详解】
A方案:
(2×2)×(2×2)×2+(2×2)×2×4
=32+32
=64(dm2)
B方案:
(2×4)×2×4+2×2×2
=64+8
=72(dm2)
因为64dm2<72dm2,所以A方案比较节省包装纸。
答:A方案比较节省包装纸。至少需要64dm2包装纸。
【点睛】
考查了长方体表面积的实际应用,计算时要认真。
答案第1页,共2页
答案第1页,共2页
