人教版六年级下册数学 3.1.2 圆柱的表面积 教案
文档属性
| 名称 | 人教版六年级下册数学 3.1.2 圆柱的表面积 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 240.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览




文档简介
第课时 圆柱的表面积
1.借助对圆柱体的各部分组成的认识,总结出圆柱体表面积的构成,理解表面积的含义,探索出表面积的计算公式。
2.正确地运用公式求出圆柱的侧面积和表面积。
3.根据实际情况,运用表面积公式解决实际问题,学习解决问题中的近似值的取舍。
4.培养学生在合作探究中获得解决问题的能力,树立学生探求知识的信念。
【重点】
掌握圆柱侧面积和表面积公式推导过程及计算方法。
【难点】
理解圆柱底面半径(直径)、高和侧面积之间的关系,进一步灵活运用公式解决实际问题。
【教师准备】 PPT课件。
【学生准备】 圆柱体模型,相关学具。
1.辨别下列图形,说出图形的名称。
(学生观察后,指名回答)
2.在这些图形中有立体图形,有平面图形。你能区分开吗
(注意学生区分立体图形和平面图形,建立立体空间观念)
3.圆柱的侧面沿高展开是什么形状 长是圆柱体的什么 宽是圆柱体的什么
(老师注意强调侧面与底面之间的关系)
【参考答案】 1.长方体、圆柱、正方体、圆、平行四边形 2.长方体、圆柱体、正方体是立体图形,圆和平行四边形是平面图形。 3.侧面沿高展开是一个长方形,长是圆柱底面的周长,宽是圆柱的高。
师: 同学们,我们以前学过长方体的表面积,回忆一下,表面积指的是什么
预设 生:长方体的表面积指的是长方体的表面面积的总和。
师:利用这个解释,想想圆柱体的表面积指的是什么。
预设 生:圆柱的两个底面面积和侧面面积的总和。
师:这节课我们就来探讨一下圆柱体的表面积。(板书课题:圆柱的表面积)
由联系旧知识的谈话导入,使学生通过已有知识联系新知识,对于学习的开始没有陌生感,自然地进入学习状态。
师:圆柱的表面积指的是什么
预设 生:圆柱的表面积指的是圆柱的两个底面面积和侧面面积的总和。
师:下面我们就来学习圆柱的表面积。(板书课题:圆柱的表面积)
直接导入,开门见山地直进主题,使学生对本节课的知识清楚明了,集中注意力展开本节课的学习。
一、探究学习圆柱体的表面积公式。
1.引导学生理解圆柱表面积的意义。
(1)拿出手中的学具,拆拆、分分,理解圆柱的表面积的意义。
师:拿出你手中的自制学具圆柱,动手拆拆,看看圆柱是由哪几部分组成的。
(学生动手操作,教师巡回指导,引导学生在操作过程中注意圆柱的组成)
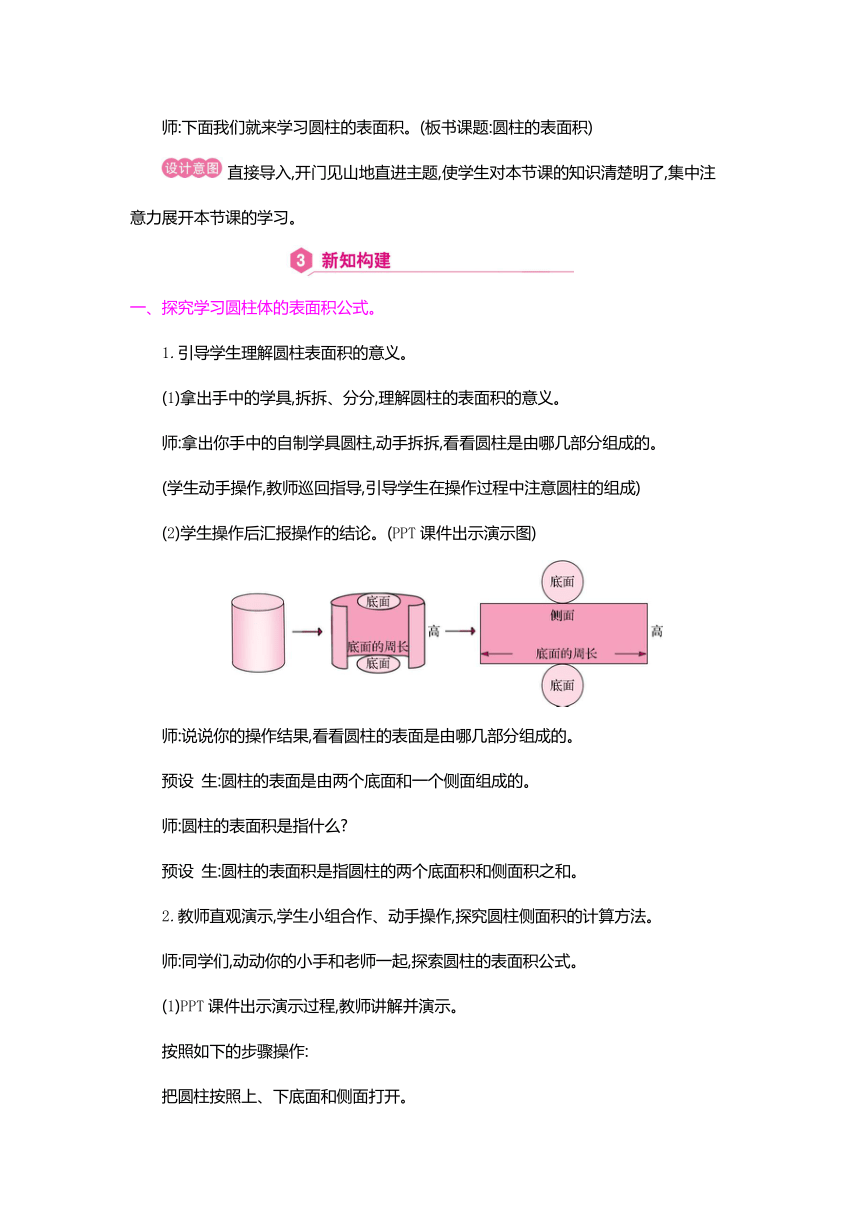
(2)学生操作后汇报操作的结论。(PPT课件出示演示图)
师:说说你的操作结果,看看圆柱的表面是由哪几部分组成的。
预设 生:圆柱的表面是由两个底面和一个侧面组成的。
师:圆柱的表面积是指什么
预设 生:圆柱的表面积是指圆柱的两个底面积和侧面积之和。
2.教师直观演示,学生小组合作、动手操作,探究圆柱侧面积的计算方法。
师:同学们,动动你的小手和老师一起,探索圆柱的表面积公式。
(1)PPT课件出示演示过程,教师讲解并演示。
按照如下的步骤操作:
把圆柱按照上、下底面和侧面打开。
(2)学生按照教师讲述的步骤操作。
(3)师生探讨侧面积的求法。
师:想想,展开的侧面是一个什么图形,怎样计算它的面积
预设 生:展开的侧面是一个长方形,长方形的面积=长×宽。
师:回忆上节课,长方形的长就是圆柱的什么 长方形的宽就是圆柱的什么
预设 生:长方形的长就是圆柱底面周长,长方形的宽就是圆柱的高。
师:综合上面的回忆和我们的理解,与同桌商议一下,得出圆柱体的侧面积公式吧!
(与同桌商议后得出侧面积公式)
预设 生:圆柱的侧面积=长方形面积=长×宽=圆柱的底面周长×高。
师:圆柱的侧面沿高展开就是一个长方形,长方形的面积是长×宽,长就是圆柱的底面周长,宽就是高,所以得出结论:
圆柱的侧面积=圆柱的底面周长×高=πdh=2πrh。
(教师适时板书)
(4)学生根据以上分析,得出圆柱体表面积公式。
师:刚才我们得到了圆柱体的侧面积公式,想想表面积公式怎么表示。
预设 生:圆柱表面积=侧面积+两个底面积。
师:用字母表示呢
预设 生:圆柱表面积:S=πdh+2πr2=2πrh+2πr2。(教师板书)
二、利用圆柱的表面积公式,解决实际生活中的问题。
(1)教师出示教材例4,指名学生读题,学生思考问题。
一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm。做这样一顶帽子至少要用多少平方厘米的面料 (得数保留整十数)
(2)读题后,教师提出问题,学生思考。
师:想求厨师的帽子需要多少平方厘米的面料,实际上就是求圆柱的什么呢
预设 生:实际上就是求圆柱的表面积。
师:厨师圆柱形的帽子表面都有哪几个面呢
(同桌讨论,交流讨论结果)
预设 生:因为帽子没有下底,所以只是求出侧面积加上一个底面面积。
(3)学生自由列式解答,教师巡回指导,汇报解答结果。
预设 生1:老师,我是这样列式的,先求出帽子的侧面积:3.14×20×30=1884(cm2)
帽顶的面积:3.14×(20÷2)2=314(cm2)
帽子用的面料:1884+314=2198(cm2)
生2:老师,我用的是综合算式:
3.14×20×30+3.14×(20÷2)2
=1884+314
=2198(cm2)
(4)师生探讨结果的“进一法”取值。
师:想一想,同学们平常买布的时候有没有按照刚好需要的面料的多少去买
预设 生:没有。
师:都是按照什么单位买布的呢
预设 生:一般都是按照米或者尺买布。
师:那我们应该精确到多少
(学生思考片刻回答)
预设 生:得数保留整十数,也就是应该大约是2200 cm2。
师:为什么必须用“进一法”
预设 生:不管计算结果最后一位是比四小,还是比五大,都进一,因为制作的时候少一点布都不够做成帽子。
引导学生在合作探究中找到解决问题的方法,体会圆柱体表面积公式在实际生活中的具体应用,在合作中提高发现问题、解决问题的能力,促进学生良好数学思维的形成。
练习1
1.教材第21页“做一做”。
2.教材第22页“做一做”第1题。
3.教材第22页“做一做”第2题。
【参考答案】 1.3.14×2×5×20=628(cm2)
2.(1)1.6×0.7=1.12(m2) (2)2×3.14×3.2×5=100.48(dm2) 3.3.14×8×13+3.14×(8÷2)2=376.8(cm2)
练习2
完成相关习题。
师:通过这节课的学习,你有什么收获
预设 生1:我学会了圆柱体表面积公式的推导过程:圆柱的侧面积=圆柱的底面周长×高,圆柱表面积=侧面积+两个底面积,即S=πdh+2πr2。
生2:我学会了用圆柱体的表面积公式去解决实际问题。
生3:我理解了在实际问题中的“进一法”。
师:我们每天都在现实生活中遇到很多问题,需要结合实际,运用我们所学知识,帮助我们更好适应生活和学习。
作业1
教材第23页练习四第1,2,3,4,5,6,7题。
作业2
完成相关习题。
圆柱的表面积 圆柱的侧面积=圆柱的底面周长×高 圆柱的表面积:S=πdh+2πr2 例4 3.14×20×30+3.14×(20÷2)2 =1884+314 =2198≈2200(cm2) 答:做这样一顶帽子至少用2200 cm2的面料。
1.本节课的教学是在“圆柱的认识”的基础上进行的,通过动手操作、直观演示、小组合作探究等学习方式,使学生探索出圆柱的表面积公式的同时理解公式推导过程,掌握推导公式的正确方法,发展学生的空间思维能力和实践能力。在理论联系实际的基础上,解决实际生活中出现的问题,锻炼学生发现问题、解决问题的能力,注重教会学生在实际生活中怎样理解“进一法”,这有利于帮助学生解决今后实际生活中出现的问题,从而也提高了学生的实践能力,通过数学知识激发学生热爱生活的情感。
2.掌握理论联系实际的学习方法在解决问题中的具体应用,使学生在树立空间思维的同时,社会生活的实践能力进一步增强。
1.由于学生涉及社会生活的机会不多,所以在解决问题的时候,思维有局限性,理解不到位,“进一法”和“四舍五入法”在实践中容易不会运用。
2.在探究过程中由于课堂的局限性,学习过程不活跃。
再教这个内容时,教师应多给学生安排一些实践性的活动,这样学生对于生活中的事情和解决问题能够有机联系,思维广泛发展,再教问题就不会混淆,课堂学习更加顺畅。教师把课堂交给学生,能够使学生的思维不受局限,自由思考,自主学习。
一个圆柱底面直径是0.5 m,高是1.8 m,求它的侧面积。(得数保留两位小数)
[名师点拨] 根据公式C=πd先求出圆柱的底面周长,再根据侧面积公式S=Ch进行计算,求出圆柱的侧面积。
[解答] 3.14×0.5×1.8
=1.57×1.8
≈2.83(m2)
答:它的侧面积约是2.83 m2。
【知识拓展】 求圆柱的侧面积,可根据实际情况,用下面的公式来计算。
S侧= C h(已知底面周长和高)
↓
S侧= πd h(已知底面直径和高)
↓
S侧= 2πr h(已知底面半径和高)
分面包
面包师傅将一个底面直径是10厘米、高是15厘米的圆柱形大面包平均分给阿丰和阿富两兄弟,面包的表面都要抹一层果酱,怎样切既能使兄弟俩满意,又能让面包师傅省一点果酱呢 请你帮面包师傅想想办法吧!(只允许横着切或竖着切)
【参考答案】 有两种切法。第一种切法:平行于底面切,切成两个完全相同的圆柱,每个圆柱的表面积包括上、下两个圆的面积和大圆柱侧面积的一半(即底面直径为10厘米,高为7.5厘米的圆柱侧面积),所以它的表面积是3.14×(10÷2)2×2+3.14×10×(15÷2)=392.5(平方厘米)。第二种切法:沿着底面直径垂直于底面切,每个半圆柱的表面积包括上、下两个半圆(相当于一个整圆)的面积、圆柱的半个侧面面积和一个长方形的面积,所以它的表面积是15×10+3.14×(10÷2)2+3.14×10×15÷2=150+78.5+235.5=464(平方厘米)。要使兄弟俩满意,又能让面包师傅省一点果酱,应采用第一种切法。
蜡烛为什么要做成圆柱形
蜡烛要做成圆柱形的原因,主要有两个:
(1)从制造工艺的角度看,圆柱形最简单方便。
(2)从实用效果看,我们知道,蜡烛在点燃过程中,烛心火焰的热量逐渐把周围的蜡熔化,圆柱形周围的蜡与烛心的火焰等距离,因此蜡烛的熔化是均匀的。如果做成其他形状的棱柱,那么烛心火焰到边和角的距离就不同,离烛心近的边上的蜡先熔化,离烛心较远的角上的蜡就熔化慢,甚至不熔化,造成浪费.
1.借助对圆柱体的各部分组成的认识,总结出圆柱体表面积的构成,理解表面积的含义,探索出表面积的计算公式。
2.正确地运用公式求出圆柱的侧面积和表面积。
3.根据实际情况,运用表面积公式解决实际问题,学习解决问题中的近似值的取舍。
4.培养学生在合作探究中获得解决问题的能力,树立学生探求知识的信念。
【重点】
掌握圆柱侧面积和表面积公式推导过程及计算方法。
【难点】
理解圆柱底面半径(直径)、高和侧面积之间的关系,进一步灵活运用公式解决实际问题。
【教师准备】 PPT课件。
【学生准备】 圆柱体模型,相关学具。
1.辨别下列图形,说出图形的名称。
(学生观察后,指名回答)
2.在这些图形中有立体图形,有平面图形。你能区分开吗
(注意学生区分立体图形和平面图形,建立立体空间观念)
3.圆柱的侧面沿高展开是什么形状 长是圆柱体的什么 宽是圆柱体的什么
(老师注意强调侧面与底面之间的关系)
【参考答案】 1.长方体、圆柱、正方体、圆、平行四边形 2.长方体、圆柱体、正方体是立体图形,圆和平行四边形是平面图形。 3.侧面沿高展开是一个长方形,长是圆柱底面的周长,宽是圆柱的高。
师: 同学们,我们以前学过长方体的表面积,回忆一下,表面积指的是什么
预设 生:长方体的表面积指的是长方体的表面面积的总和。
师:利用这个解释,想想圆柱体的表面积指的是什么。
预设 生:圆柱的两个底面面积和侧面面积的总和。
师:这节课我们就来探讨一下圆柱体的表面积。(板书课题:圆柱的表面积)
由联系旧知识的谈话导入,使学生通过已有知识联系新知识,对于学习的开始没有陌生感,自然地进入学习状态。
师:圆柱的表面积指的是什么
预设 生:圆柱的表面积指的是圆柱的两个底面面积和侧面面积的总和。
师:下面我们就来学习圆柱的表面积。(板书课题:圆柱的表面积)
直接导入,开门见山地直进主题,使学生对本节课的知识清楚明了,集中注意力展开本节课的学习。
一、探究学习圆柱体的表面积公式。
1.引导学生理解圆柱表面积的意义。
(1)拿出手中的学具,拆拆、分分,理解圆柱的表面积的意义。
师:拿出你手中的自制学具圆柱,动手拆拆,看看圆柱是由哪几部分组成的。
(学生动手操作,教师巡回指导,引导学生在操作过程中注意圆柱的组成)
(2)学生操作后汇报操作的结论。(PPT课件出示演示图)
师:说说你的操作结果,看看圆柱的表面是由哪几部分组成的。
预设 生:圆柱的表面是由两个底面和一个侧面组成的。
师:圆柱的表面积是指什么
预设 生:圆柱的表面积是指圆柱的两个底面积和侧面积之和。
2.教师直观演示,学生小组合作、动手操作,探究圆柱侧面积的计算方法。
师:同学们,动动你的小手和老师一起,探索圆柱的表面积公式。
(1)PPT课件出示演示过程,教师讲解并演示。
按照如下的步骤操作:
把圆柱按照上、下底面和侧面打开。
(2)学生按照教师讲述的步骤操作。
(3)师生探讨侧面积的求法。
师:想想,展开的侧面是一个什么图形,怎样计算它的面积
预设 生:展开的侧面是一个长方形,长方形的面积=长×宽。
师:回忆上节课,长方形的长就是圆柱的什么 长方形的宽就是圆柱的什么
预设 生:长方形的长就是圆柱底面周长,长方形的宽就是圆柱的高。
师:综合上面的回忆和我们的理解,与同桌商议一下,得出圆柱体的侧面积公式吧!
(与同桌商议后得出侧面积公式)
预设 生:圆柱的侧面积=长方形面积=长×宽=圆柱的底面周长×高。
师:圆柱的侧面沿高展开就是一个长方形,长方形的面积是长×宽,长就是圆柱的底面周长,宽就是高,所以得出结论:
圆柱的侧面积=圆柱的底面周长×高=πdh=2πrh。
(教师适时板书)
(4)学生根据以上分析,得出圆柱体表面积公式。
师:刚才我们得到了圆柱体的侧面积公式,想想表面积公式怎么表示。
预设 生:圆柱表面积=侧面积+两个底面积。
师:用字母表示呢
预设 生:圆柱表面积:S=πdh+2πr2=2πrh+2πr2。(教师板书)
二、利用圆柱的表面积公式,解决实际生活中的问题。
(1)教师出示教材例4,指名学生读题,学生思考问题。
一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm。做这样一顶帽子至少要用多少平方厘米的面料 (得数保留整十数)
(2)读题后,教师提出问题,学生思考。
师:想求厨师的帽子需要多少平方厘米的面料,实际上就是求圆柱的什么呢
预设 生:实际上就是求圆柱的表面积。
师:厨师圆柱形的帽子表面都有哪几个面呢
(同桌讨论,交流讨论结果)
预设 生:因为帽子没有下底,所以只是求出侧面积加上一个底面面积。
(3)学生自由列式解答,教师巡回指导,汇报解答结果。
预设 生1:老师,我是这样列式的,先求出帽子的侧面积:3.14×20×30=1884(cm2)
帽顶的面积:3.14×(20÷2)2=314(cm2)
帽子用的面料:1884+314=2198(cm2)
生2:老师,我用的是综合算式:
3.14×20×30+3.14×(20÷2)2
=1884+314
=2198(cm2)
(4)师生探讨结果的“进一法”取值。
师:想一想,同学们平常买布的时候有没有按照刚好需要的面料的多少去买
预设 生:没有。
师:都是按照什么单位买布的呢
预设 生:一般都是按照米或者尺买布。
师:那我们应该精确到多少
(学生思考片刻回答)
预设 生:得数保留整十数,也就是应该大约是2200 cm2。
师:为什么必须用“进一法”
预设 生:不管计算结果最后一位是比四小,还是比五大,都进一,因为制作的时候少一点布都不够做成帽子。
引导学生在合作探究中找到解决问题的方法,体会圆柱体表面积公式在实际生活中的具体应用,在合作中提高发现问题、解决问题的能力,促进学生良好数学思维的形成。
练习1
1.教材第21页“做一做”。
2.教材第22页“做一做”第1题。
3.教材第22页“做一做”第2题。
【参考答案】 1.3.14×2×5×20=628(cm2)
2.(1)1.6×0.7=1.12(m2) (2)2×3.14×3.2×5=100.48(dm2) 3.3.14×8×13+3.14×(8÷2)2=376.8(cm2)
练习2
完成相关习题。
师:通过这节课的学习,你有什么收获
预设 生1:我学会了圆柱体表面积公式的推导过程:圆柱的侧面积=圆柱的底面周长×高,圆柱表面积=侧面积+两个底面积,即S=πdh+2πr2。
生2:我学会了用圆柱体的表面积公式去解决实际问题。
生3:我理解了在实际问题中的“进一法”。
师:我们每天都在现实生活中遇到很多问题,需要结合实际,运用我们所学知识,帮助我们更好适应生活和学习。
作业1
教材第23页练习四第1,2,3,4,5,6,7题。
作业2
完成相关习题。
圆柱的表面积 圆柱的侧面积=圆柱的底面周长×高 圆柱的表面积:S=πdh+2πr2 例4 3.14×20×30+3.14×(20÷2)2 =1884+314 =2198≈2200(cm2) 答:做这样一顶帽子至少用2200 cm2的面料。
1.本节课的教学是在“圆柱的认识”的基础上进行的,通过动手操作、直观演示、小组合作探究等学习方式,使学生探索出圆柱的表面积公式的同时理解公式推导过程,掌握推导公式的正确方法,发展学生的空间思维能力和实践能力。在理论联系实际的基础上,解决实际生活中出现的问题,锻炼学生发现问题、解决问题的能力,注重教会学生在实际生活中怎样理解“进一法”,这有利于帮助学生解决今后实际生活中出现的问题,从而也提高了学生的实践能力,通过数学知识激发学生热爱生活的情感。
2.掌握理论联系实际的学习方法在解决问题中的具体应用,使学生在树立空间思维的同时,社会生活的实践能力进一步增强。
1.由于学生涉及社会生活的机会不多,所以在解决问题的时候,思维有局限性,理解不到位,“进一法”和“四舍五入法”在实践中容易不会运用。
2.在探究过程中由于课堂的局限性,学习过程不活跃。
再教这个内容时,教师应多给学生安排一些实践性的活动,这样学生对于生活中的事情和解决问题能够有机联系,思维广泛发展,再教问题就不会混淆,课堂学习更加顺畅。教师把课堂交给学生,能够使学生的思维不受局限,自由思考,自主学习。
一个圆柱底面直径是0.5 m,高是1.8 m,求它的侧面积。(得数保留两位小数)
[名师点拨] 根据公式C=πd先求出圆柱的底面周长,再根据侧面积公式S=Ch进行计算,求出圆柱的侧面积。
[解答] 3.14×0.5×1.8
=1.57×1.8
≈2.83(m2)
答:它的侧面积约是2.83 m2。
【知识拓展】 求圆柱的侧面积,可根据实际情况,用下面的公式来计算。
S侧= C h(已知底面周长和高)
↓
S侧= πd h(已知底面直径和高)
↓
S侧= 2πr h(已知底面半径和高)
分面包
面包师傅将一个底面直径是10厘米、高是15厘米的圆柱形大面包平均分给阿丰和阿富两兄弟,面包的表面都要抹一层果酱,怎样切既能使兄弟俩满意,又能让面包师傅省一点果酱呢 请你帮面包师傅想想办法吧!(只允许横着切或竖着切)
【参考答案】 有两种切法。第一种切法:平行于底面切,切成两个完全相同的圆柱,每个圆柱的表面积包括上、下两个圆的面积和大圆柱侧面积的一半(即底面直径为10厘米,高为7.5厘米的圆柱侧面积),所以它的表面积是3.14×(10÷2)2×2+3.14×10×(15÷2)=392.5(平方厘米)。第二种切法:沿着底面直径垂直于底面切,每个半圆柱的表面积包括上、下两个半圆(相当于一个整圆)的面积、圆柱的半个侧面面积和一个长方形的面积,所以它的表面积是15×10+3.14×(10÷2)2+3.14×10×15÷2=150+78.5+235.5=464(平方厘米)。要使兄弟俩满意,又能让面包师傅省一点果酱,应采用第一种切法。
蜡烛为什么要做成圆柱形
蜡烛要做成圆柱形的原因,主要有两个:
(1)从制造工艺的角度看,圆柱形最简单方便。
(2)从实用效果看,我们知道,蜡烛在点燃过程中,烛心火焰的热量逐渐把周围的蜡熔化,圆柱形周围的蜡与烛心的火焰等距离,因此蜡烛的熔化是均匀的。如果做成其他形状的棱柱,那么烛心火焰到边和角的距离就不同,离烛心近的边上的蜡先熔化,离烛心较远的角上的蜡就熔化慢,甚至不熔化,造成浪费.
