人教版数学六年级下册 总复习 数学思考 教案
文档属性
| 名称 | 人教版数学六年级下册 总复习 数学思考 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 211.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 20:41:02 | ||
图片预览




文档简介
4 数学思考
本节课所涉及的数学思考部分是让学生通过这些内容的学习,在推理方面得到更多的训练,进一步发展逻辑推理能力和解决问题的能力。教材中本部分的内容包括利用数形结合找规律、列表推理、等量代换、简单的几何证明,都是发展学生逻辑推理能力的典型素材。
在这部分的教学中要使学生进一步掌握观察、枚举、比较、归纳、列表、假设等逻辑推理时常用的方法,并能较灵活地运用所学方法解决一些实际问题。使学生体会逻辑推理是数学学习和解决问题的一种重要思考方式,培养学生的逻辑推理能力和解决问题的能力。在教学中使学生感受数学学习的魅力,激发学生学习兴趣的愿望,培养学生学习数学的兴趣。
1.使学生进一步掌握观察、枚举、比较、归纳、列表、假设等逻辑推理时常用的方法,并能较灵活地运用所学方法解决一些实际问题。
2.使学生体会逻辑推理是数学学习和解决问题的一种重要思考方式,培养学生的逻辑推理能力和解决问题的能力。
3.使学生感受数学学习的魅力,激发学生学习数学的兴趣。
【重点】
使学生进一步掌握观察、枚举、比较、归纳、列表、假设等逻辑推理时常用的方法,并能较灵活地运用所学方法解决一些实际问题。
【难点】
使学生体会逻辑推理是数学学习和解决问题的一种重要思考方式,培养学生的逻辑推理能力和解决问题的能力。
【教师准备】 PPT课件。
师:同学们,你们观察过周围的事物吗
预设 生:观察过。
师:想想哪些事物是有规律的。说一说。
预设 生1:一天当中的早上、中午、晚上。
生2:人的生老病死。
生3:数字的变化。
师:这里面都包含着数学问题,今天就和老师一起对这些数学问题进行思考。(教师板书课题)
联系生活实际导入,通过学生生活中常见的话题导入,使学生在平和融洽的氛围中走进本节课的学习。
师:回忆我们学过的知识,想想我们用什么方法在数学问题中发现问题和解决问题的。
预设 生1:根据数字找规律。
生2:图形找规律。
师:今天我们将系统地学习这些有关数学思考的问题。(教师板书课题)
回忆知识导入,在回忆中帮助学生回忆旧知识联系新知识,使教学有一个良好的开端。
师:今天和老师一起来学习数学思考的实践活动。(教师板书课题)
开门见山地直接导入,使学生直截了当地知道本节课的知识要点,使主题更加鲜明。
考点1 找规律
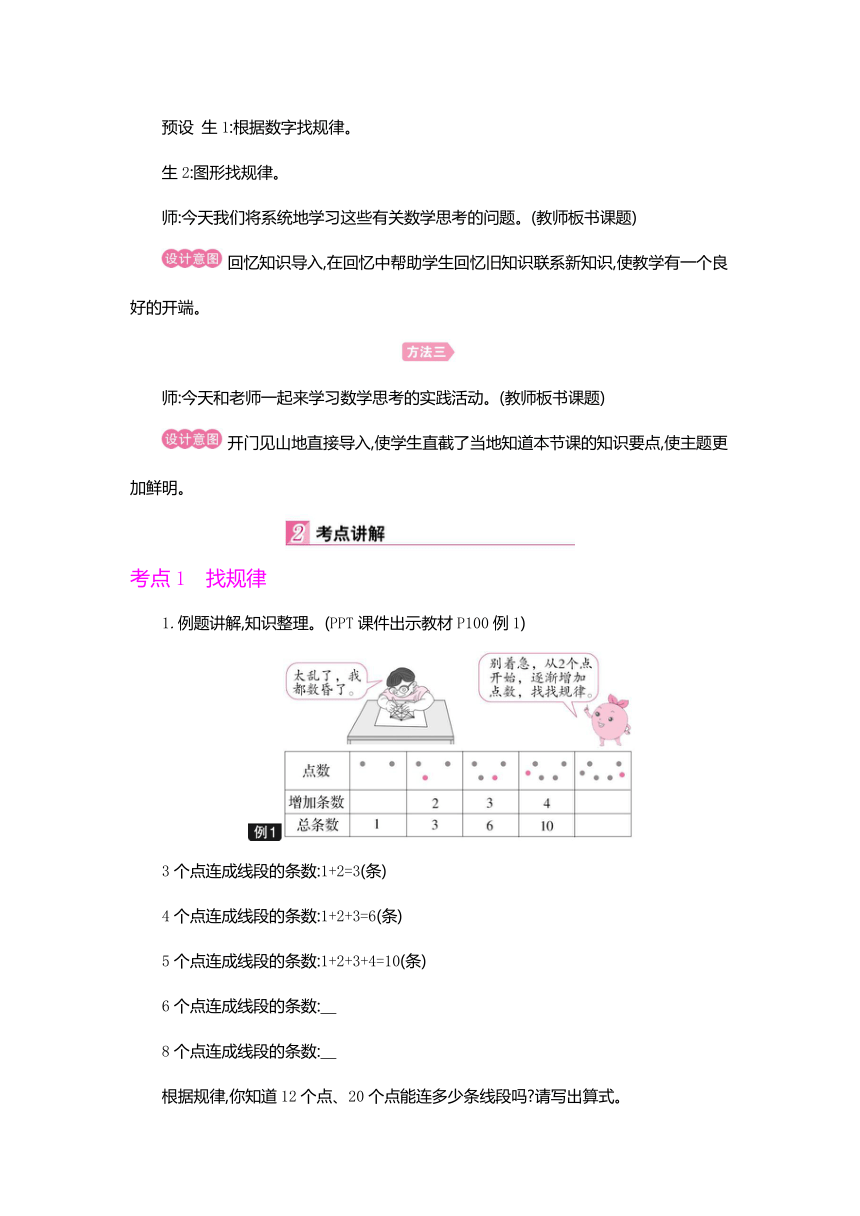
1.例题讲解,知识整理。(PPT课件出示教材P100例1)
3个点连成线段的条数:1+2=3(条)
4个点连成线段的条数:1+2+3=6(条)
5个点连成线段的条数:1+2+3+4=10(条)
6个点连成线段的条数:
8个点连成线段的条数:
根据规律,你知道12个点、20个点能连多少条线段吗 请写出算式。
想一想,n个点能连多少条线段
(1)师:今天我们来复习找规律的相关知识,这样类型的习题大家还会解答吧 首先我们来计算一下图中3个点、4个点和5个点连成的线段的条数,自己完成。
预设 生1:3个点连成线段的条数是3条。
生2:4个点连成线段的条数是6条。
生3:5个点连成线段的条数是10条。
(2)师:你是怎样分别列式计算出来的
预设 生:3个点:1+2=3(条),
4个点:1+2+3=6(条),
5个点:1+2+3+4=10(条)。
师:通过观察,你发现了什么规律呢
预设 生:每次计算的时候都是从1开始加,加到比点数少1的数字,比如:5个点连成的线段条数是:1+2+3+4=10(条)。
(3)师:那么按照这个规律,6个点和8个点连成的线段条数应该怎么计算呢
预设 生1:6个点:1+2+3+4+5=15(条)。
生2:8个点:1+2+3+4+5+6+7=28(条)。
(4)师:那么按照刚才找到的规律,12个点、20个点能连成多少条线段呢 自己写出算式,不用计算。
预设 生1:12个点:1+2+3+4+5+6+7+8+9+10+11。
生2:20个点:1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19。
师:按照这个规律,n个点能连成多少条线段
预设 生:n个点:1+2+3+…+(n-1)。(板书)
师:我们也可以用公式:n(n-1)来计算,其中n表示点的个数。
2.巩固练习。
师:刚才我们复习了找规律的相关知识,现在我们来检测一下学习成果。
PPT课件出示教材P100做一做。
观察下图,想一想。
(1)第7幅图有多少个棋子 第15幅图呢
…
(1) (2) (3) (4)
(2)*第n幅图有多少个棋子
引导学生观察图的序号和棋子个数的关系,可以得出:第1幅图棋子的个数是:1=1×1,第2幅图棋子的个数是:4=2×2,第3幅图棋子的个数是:9=3×3,第4幅图棋子的个数是:16=4×4,那么可以推出第7幅图有49个棋子,第15幅图棋子的个数是:15×15,进而推导出:第n幅图有n×n个棋子。
【参考答案】 (1)49个,225个。 (2)n×n个或n2个。
考点2 列表推理
1.例题讲解,知识整理。(PPT课件出示教材P101例2)
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A,B,C;第二次有B,D,E;第三次有A,E,F。请问:哪两位班长是同班的
(1)师:今天我们来继续复习列表推理的相关知识,这样类型的习题大家还会解答吧 首先我们看可以怎样推理呢
预设 生:可以用列表推理的方式来进行。
师:对,我们可以用数字“1”表示到会,用数字“0”表示没到会。自己完成表格。
(2)学生汇报学习成果,共同列表。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
(3)师:我们在推理时,哪个条件是非常重要的
预设 生:每次每班只要一个班长参加。
师:也就是说,每个班长只能和其他班的班长同时出现。
师:通过上表,可能推出哪两位班长是同班的 怎么推理的呢
预设 生1:从第一次到会的情况可以看出,A只可能和D,E,F同班。
生2:从第二次到会的情况可以判断,A只可能和D,E同班。
生3:从第三次到会的情况可以确定,A只可能和D同班。
(4)学生小组合作,用刚才的方法,自己推出B,C分别与谁同班。
(5)学生汇报推导结果:
师:你是如何来判断B和谁是同班的
预设 生1:从第一次到会的情况可以看出,B只可能和D,E,F同班。
生2:从第二次到会的情况可以判断,B只可能和F同班。
师:那么同样的道理谁来说说如何判断C和谁是同班的
预设 生1:从第一次到会的情况可以看出,C只可能和D,E,F同班。
生2:从第二次到会的情况可以判断,C只可能和D,E同班。
生3:从第三次到会的情况可以确定,C只可能和E同班。
师:那么对于最后的一个判断C的情况,还有什么更直接的办法吗
预设 生:因为已经判断A和D同班、B和F同班,那么一共只有六个人,剩下的C和E就是同班了。(板书答案)
2.巩固练习。
(1)师:刚才我们复习了列表推理的相关知识,现在我们来检测一下学习成果。(PPT课件出示教材P101做一做)
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。请问:他们的职业各是什么
(2)引导学生进行分析:
师:从王阿姨是教师,丁叔叔不是工人,你可以确定哪些信息
预设 生1:可以确定王阿姨是教师。
生2:可以确定丁叔叔是军人或教师。
师:还可以怎样进一步判断丁叔叔的身份
预设 生:从“只有刘阿姨和李叔叔的职业相同”,可知丁叔叔不可能和王阿姨一样是教师,所以他是军人。
师:那么剩下怎样判断呢
预设 生:因为剩下的职业只有工人了,而刘阿姨和李叔叔的职业相同,所以刘阿姨和李叔叔都是工人。
【参考答案】 王阿姨:教师 刘阿姨:工人 丁叔叔:军人 李叔叔:工人
考点3 等量代换
例题讲解,知识整理。(PPT课件出示教材P101例3)
△、□、○、☆、 各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
(2)已知○+☆=160, +☆=160。○是否等于
(1)师:今天我们来继续复习等量代换的相关知识,这样类型的习题大家还会解答吧 首先我们看(1)是怎样来解答的。
预设 生:由题目中可知:
一个△等于三个□的和,可知△+□=4个□=24,所以□=6,△=6×3=18,师生共同总结。(板书总结)
把△+□=24中的△换成□+□+□,这叫等量代换。
(2)师:我们再来解答(2),题目中知道哪些条件 可以怎样进行推理呢
引导学生分析:
预设 生:已知○+☆=160, +☆=160。
师:根据什么来进行推断呢
预设 生:根据等式的性质,等式两边都减去☆。
可以推出○=160-☆, =160-☆ 。
因为☆代表同一个数,所以○= 。
考点4 简单的几何证明
例题讲解,知识整理。(PPT课件出示教材P102例4)
什么是平角 平角与直线有什么区别 如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平角,一共能组成几个平角
(2)你能推出∠1=∠3吗
(1)师:今天我们来继续复习简单的几何证明,首先我们看(1)是怎样来解答的呢 怎样来确定两个角组成一个平角呢
预设 生:平角的两边在一条直线上。
师:由此可以判断哪几个角组成平角
预设 生:∠1和∠2,∠2和∠3,∠3和∠4,∠4和∠1,都分别能组成平角,一共能组成4个平角。
(2)师:我们来看看怎么证明(2)呢 请同学以小组为单位,探讨证明的方法。
学生以小组为单位进行自学。
学生汇报学习成果:
①根据第(1)题的结论,可以得到∠1+∠2=180°,∠2+∠3=180°。
②根据等式的性质,等式的两边都减去∠2,可以得到∠1=180°-∠2,∠3=180°-∠2。
③因为180°-∠2=180°-∠2,所以∠1=∠3。(师板书学生汇报成果)
练习1
(1)PPT课件出示教材P103第1题。
(2)引导学生分析,(1)中,分别是在前一个数字的基础上加上8,9,10,那么第5个数应该是在前一个数字30的基础上加11,得41,以此类推,第6个数是41,加12,得53,第7个数是53,加13,得66。
(3)引导学生观察分析得出:(2)中奇数个数的数分别是前一个奇数个数的数的2倍,所以第9个数就是第7个数8的2倍,8×2=16,第11个数就是第9个数16的2倍,16×2=32。而偶数个数上的数分别是3的倍数,所以第8个数是4的3倍,4×3=12。
【参考答案】 (1)41 66 (2)12 16 32
练习2
完成相关习题。
师:在这节课的学习中,我们都复习了哪些知识
引导学生总结这节课复习了找规律、列表推理、等量代换和简单的几何证明等知识。
作业1
教材第103页练习二十二第2~10题。
作业2
完成相关习题。
数学思考 例1:n个点:1+2+3+…+(n-1)。 例2:A和D,B和F,C和E分别同班。 例3:把△+□=24中的△换成□+□+□,这叫等量代换。 例4:①∠1+∠2=180°,∠2+∠3=180°。 ②∠1=180°-∠2,∠3=180°-∠2。 ③180°-∠2=180°-∠2,∠1=∠3。
1.在教学中教师在关键时发挥了引导作用,在教学例1时,及时把握住了两点:一是想到每个新增的点都要与之前的点相连,二是总结发现的规律,在这个过程中,教师及时进行了引导,达到了事半功倍的效果。
2.在教学中,能够立足学生基础开展教学,在教学例4时,既然学生感觉两个角是相等的,就利用好这一教学契机,通过提问,让学生去积极主动地探索和求知。
3.及时引导学生推理的过程,学生虽然能说出原因,但是在阐述上会出现不够严密的现象,此时,适当地发挥了引领作用,借助规范的语言和板书,让学生模仿,以此体会数学的严谨性和逻辑性。
1.没能充分发挥学生的主体作用,特别是简单的几何证明部分,怕学生做不好,没有把学习的主动权完全交给学生,虽然也让学生懂得了证明的过程,但是影响了学生学习的积极性。
2.在训练学生严密推理和表述上做得不够好,没能完全做到让学生在教师指导下有根据、有步骤地进行语言表达式的推理。
再教这节课时,要扬长避短。继续发挥教师的引领作用,但是同时也要注重学生积极性的发挥,让学生多动手动脑地参与,教师适当地予以指导。
本节课所涉及的数学思考部分是让学生通过这些内容的学习,在推理方面得到更多的训练,进一步发展逻辑推理能力和解决问题的能力。教材中本部分的内容包括利用数形结合找规律、列表推理、等量代换、简单的几何证明,都是发展学生逻辑推理能力的典型素材。
在这部分的教学中要使学生进一步掌握观察、枚举、比较、归纳、列表、假设等逻辑推理时常用的方法,并能较灵活地运用所学方法解决一些实际问题。使学生体会逻辑推理是数学学习和解决问题的一种重要思考方式,培养学生的逻辑推理能力和解决问题的能力。在教学中使学生感受数学学习的魅力,激发学生学习兴趣的愿望,培养学生学习数学的兴趣。
1.使学生进一步掌握观察、枚举、比较、归纳、列表、假设等逻辑推理时常用的方法,并能较灵活地运用所学方法解决一些实际问题。
2.使学生体会逻辑推理是数学学习和解决问题的一种重要思考方式,培养学生的逻辑推理能力和解决问题的能力。
3.使学生感受数学学习的魅力,激发学生学习数学的兴趣。
【重点】
使学生进一步掌握观察、枚举、比较、归纳、列表、假设等逻辑推理时常用的方法,并能较灵活地运用所学方法解决一些实际问题。
【难点】
使学生体会逻辑推理是数学学习和解决问题的一种重要思考方式,培养学生的逻辑推理能力和解决问题的能力。
【教师准备】 PPT课件。
师:同学们,你们观察过周围的事物吗
预设 生:观察过。
师:想想哪些事物是有规律的。说一说。
预设 生1:一天当中的早上、中午、晚上。
生2:人的生老病死。
生3:数字的变化。
师:这里面都包含着数学问题,今天就和老师一起对这些数学问题进行思考。(教师板书课题)
联系生活实际导入,通过学生生活中常见的话题导入,使学生在平和融洽的氛围中走进本节课的学习。
师:回忆我们学过的知识,想想我们用什么方法在数学问题中发现问题和解决问题的。
预设 生1:根据数字找规律。
生2:图形找规律。
师:今天我们将系统地学习这些有关数学思考的问题。(教师板书课题)
回忆知识导入,在回忆中帮助学生回忆旧知识联系新知识,使教学有一个良好的开端。
师:今天和老师一起来学习数学思考的实践活动。(教师板书课题)
开门见山地直接导入,使学生直截了当地知道本节课的知识要点,使主题更加鲜明。
考点1 找规律
1.例题讲解,知识整理。(PPT课件出示教材P100例1)
3个点连成线段的条数:1+2=3(条)
4个点连成线段的条数:1+2+3=6(条)
5个点连成线段的条数:1+2+3+4=10(条)
6个点连成线段的条数:
8个点连成线段的条数:
根据规律,你知道12个点、20个点能连多少条线段吗 请写出算式。
想一想,n个点能连多少条线段
(1)师:今天我们来复习找规律的相关知识,这样类型的习题大家还会解答吧 首先我们来计算一下图中3个点、4个点和5个点连成的线段的条数,自己完成。
预设 生1:3个点连成线段的条数是3条。
生2:4个点连成线段的条数是6条。
生3:5个点连成线段的条数是10条。
(2)师:你是怎样分别列式计算出来的
预设 生:3个点:1+2=3(条),
4个点:1+2+3=6(条),
5个点:1+2+3+4=10(条)。
师:通过观察,你发现了什么规律呢
预设 生:每次计算的时候都是从1开始加,加到比点数少1的数字,比如:5个点连成的线段条数是:1+2+3+4=10(条)。
(3)师:那么按照这个规律,6个点和8个点连成的线段条数应该怎么计算呢
预设 生1:6个点:1+2+3+4+5=15(条)。
生2:8个点:1+2+3+4+5+6+7=28(条)。
(4)师:那么按照刚才找到的规律,12个点、20个点能连成多少条线段呢 自己写出算式,不用计算。
预设 生1:12个点:1+2+3+4+5+6+7+8+9+10+11。
生2:20个点:1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19。
师:按照这个规律,n个点能连成多少条线段
预设 生:n个点:1+2+3+…+(n-1)。(板书)
师:我们也可以用公式:n(n-1)来计算,其中n表示点的个数。
2.巩固练习。
师:刚才我们复习了找规律的相关知识,现在我们来检测一下学习成果。
PPT课件出示教材P100做一做。
观察下图,想一想。
(1)第7幅图有多少个棋子 第15幅图呢
…
(1) (2) (3) (4)
(2)*第n幅图有多少个棋子
引导学生观察图的序号和棋子个数的关系,可以得出:第1幅图棋子的个数是:1=1×1,第2幅图棋子的个数是:4=2×2,第3幅图棋子的个数是:9=3×3,第4幅图棋子的个数是:16=4×4,那么可以推出第7幅图有49个棋子,第15幅图棋子的个数是:15×15,进而推导出:第n幅图有n×n个棋子。
【参考答案】 (1)49个,225个。 (2)n×n个或n2个。
考点2 列表推理
1.例题讲解,知识整理。(PPT课件出示教材P101例2)
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A,B,C;第二次有B,D,E;第三次有A,E,F。请问:哪两位班长是同班的
(1)师:今天我们来继续复习列表推理的相关知识,这样类型的习题大家还会解答吧 首先我们看可以怎样推理呢
预设 生:可以用列表推理的方式来进行。
师:对,我们可以用数字“1”表示到会,用数字“0”表示没到会。自己完成表格。
(2)学生汇报学习成果,共同列表。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
(3)师:我们在推理时,哪个条件是非常重要的
预设 生:每次每班只要一个班长参加。
师:也就是说,每个班长只能和其他班的班长同时出现。
师:通过上表,可能推出哪两位班长是同班的 怎么推理的呢
预设 生1:从第一次到会的情况可以看出,A只可能和D,E,F同班。
生2:从第二次到会的情况可以判断,A只可能和D,E同班。
生3:从第三次到会的情况可以确定,A只可能和D同班。
(4)学生小组合作,用刚才的方法,自己推出B,C分别与谁同班。
(5)学生汇报推导结果:
师:你是如何来判断B和谁是同班的
预设 生1:从第一次到会的情况可以看出,B只可能和D,E,F同班。
生2:从第二次到会的情况可以判断,B只可能和F同班。
师:那么同样的道理谁来说说如何判断C和谁是同班的
预设 生1:从第一次到会的情况可以看出,C只可能和D,E,F同班。
生2:从第二次到会的情况可以判断,C只可能和D,E同班。
生3:从第三次到会的情况可以确定,C只可能和E同班。
师:那么对于最后的一个判断C的情况,还有什么更直接的办法吗
预设 生:因为已经判断A和D同班、B和F同班,那么一共只有六个人,剩下的C和E就是同班了。(板书答案)
2.巩固练习。
(1)师:刚才我们复习了列表推理的相关知识,现在我们来检测一下学习成果。(PPT课件出示教材P101做一做)
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。请问:他们的职业各是什么
(2)引导学生进行分析:
师:从王阿姨是教师,丁叔叔不是工人,你可以确定哪些信息
预设 生1:可以确定王阿姨是教师。
生2:可以确定丁叔叔是军人或教师。
师:还可以怎样进一步判断丁叔叔的身份
预设 生:从“只有刘阿姨和李叔叔的职业相同”,可知丁叔叔不可能和王阿姨一样是教师,所以他是军人。
师:那么剩下怎样判断呢
预设 生:因为剩下的职业只有工人了,而刘阿姨和李叔叔的职业相同,所以刘阿姨和李叔叔都是工人。
【参考答案】 王阿姨:教师 刘阿姨:工人 丁叔叔:军人 李叔叔:工人
考点3 等量代换
例题讲解,知识整理。(PPT课件出示教材P101例3)
△、□、○、☆、 各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
(2)已知○+☆=160, +☆=160。○是否等于
(1)师:今天我们来继续复习等量代换的相关知识,这样类型的习题大家还会解答吧 首先我们看(1)是怎样来解答的。
预设 生:由题目中可知:
一个△等于三个□的和,可知△+□=4个□=24,所以□=6,△=6×3=18,师生共同总结。(板书总结)
把△+□=24中的△换成□+□+□,这叫等量代换。
(2)师:我们再来解答(2),题目中知道哪些条件 可以怎样进行推理呢
引导学生分析:
预设 生:已知○+☆=160, +☆=160。
师:根据什么来进行推断呢
预设 生:根据等式的性质,等式两边都减去☆。
可以推出○=160-☆, =160-☆ 。
因为☆代表同一个数,所以○= 。
考点4 简单的几何证明
例题讲解,知识整理。(PPT课件出示教材P102例4)
什么是平角 平角与直线有什么区别 如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平角,一共能组成几个平角
(2)你能推出∠1=∠3吗
(1)师:今天我们来继续复习简单的几何证明,首先我们看(1)是怎样来解答的呢 怎样来确定两个角组成一个平角呢
预设 生:平角的两边在一条直线上。
师:由此可以判断哪几个角组成平角
预设 生:∠1和∠2,∠2和∠3,∠3和∠4,∠4和∠1,都分别能组成平角,一共能组成4个平角。
(2)师:我们来看看怎么证明(2)呢 请同学以小组为单位,探讨证明的方法。
学生以小组为单位进行自学。
学生汇报学习成果:
①根据第(1)题的结论,可以得到∠1+∠2=180°,∠2+∠3=180°。
②根据等式的性质,等式的两边都减去∠2,可以得到∠1=180°-∠2,∠3=180°-∠2。
③因为180°-∠2=180°-∠2,所以∠1=∠3。(师板书学生汇报成果)
练习1
(1)PPT课件出示教材P103第1题。
(2)引导学生分析,(1)中,分别是在前一个数字的基础上加上8,9,10,那么第5个数应该是在前一个数字30的基础上加11,得41,以此类推,第6个数是41,加12,得53,第7个数是53,加13,得66。
(3)引导学生观察分析得出:(2)中奇数个数的数分别是前一个奇数个数的数的2倍,所以第9个数就是第7个数8的2倍,8×2=16,第11个数就是第9个数16的2倍,16×2=32。而偶数个数上的数分别是3的倍数,所以第8个数是4的3倍,4×3=12。
【参考答案】 (1)41 66 (2)12 16 32
练习2
完成相关习题。
师:在这节课的学习中,我们都复习了哪些知识
引导学生总结这节课复习了找规律、列表推理、等量代换和简单的几何证明等知识。
作业1
教材第103页练习二十二第2~10题。
作业2
完成相关习题。
数学思考 例1:n个点:1+2+3+…+(n-1)。 例2:A和D,B和F,C和E分别同班。 例3:把△+□=24中的△换成□+□+□,这叫等量代换。 例4:①∠1+∠2=180°,∠2+∠3=180°。 ②∠1=180°-∠2,∠3=180°-∠2。 ③180°-∠2=180°-∠2,∠1=∠3。
1.在教学中教师在关键时发挥了引导作用,在教学例1时,及时把握住了两点:一是想到每个新增的点都要与之前的点相连,二是总结发现的规律,在这个过程中,教师及时进行了引导,达到了事半功倍的效果。
2.在教学中,能够立足学生基础开展教学,在教学例4时,既然学生感觉两个角是相等的,就利用好这一教学契机,通过提问,让学生去积极主动地探索和求知。
3.及时引导学生推理的过程,学生虽然能说出原因,但是在阐述上会出现不够严密的现象,此时,适当地发挥了引领作用,借助规范的语言和板书,让学生模仿,以此体会数学的严谨性和逻辑性。
1.没能充分发挥学生的主体作用,特别是简单的几何证明部分,怕学生做不好,没有把学习的主动权完全交给学生,虽然也让学生懂得了证明的过程,但是影响了学生学习的积极性。
2.在训练学生严密推理和表述上做得不够好,没能完全做到让学生在教师指导下有根据、有步骤地进行语言表达式的推理。
再教这节课时,要扬长避短。继续发挥教师的引领作用,但是同时也要注重学生积极性的发挥,让学生多动手动脑地参与,教师适当地予以指导。
