28.2.1解直角三角形 课件(共13张PPT)
文档属性
| 名称 | 28.2.1解直角三角形 课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 21:13:18 | ||
图片预览



文档简介
(共13张PPT)
28.2.1解直角三角形
新人教版九年级下册
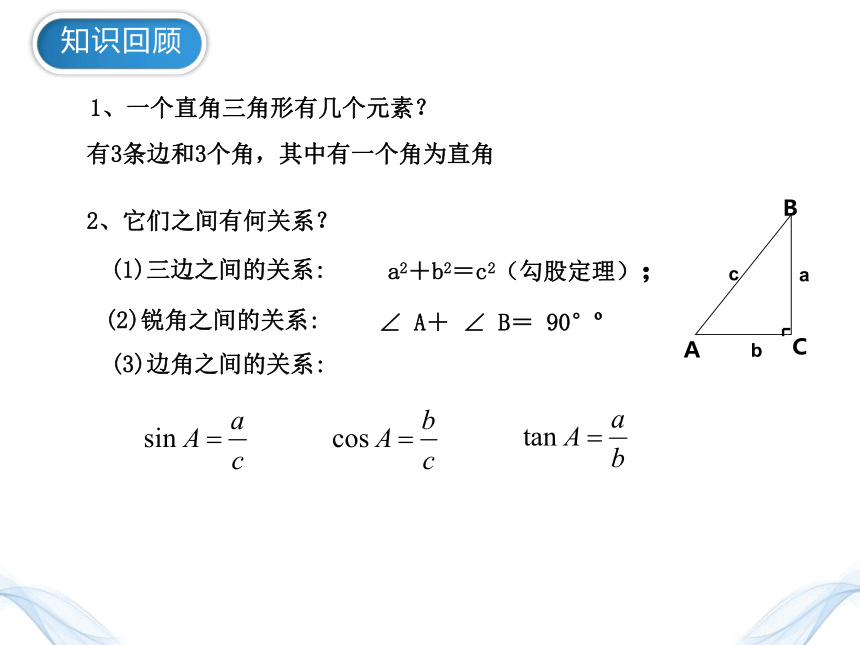
知识回顾
1、一个直角三角形有几个元素?
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90°
(3)边角之间的关系:
A
C
B
a
b
c
有3条边和3个角,其中有一个角为直角
2、它们之间有何关系?
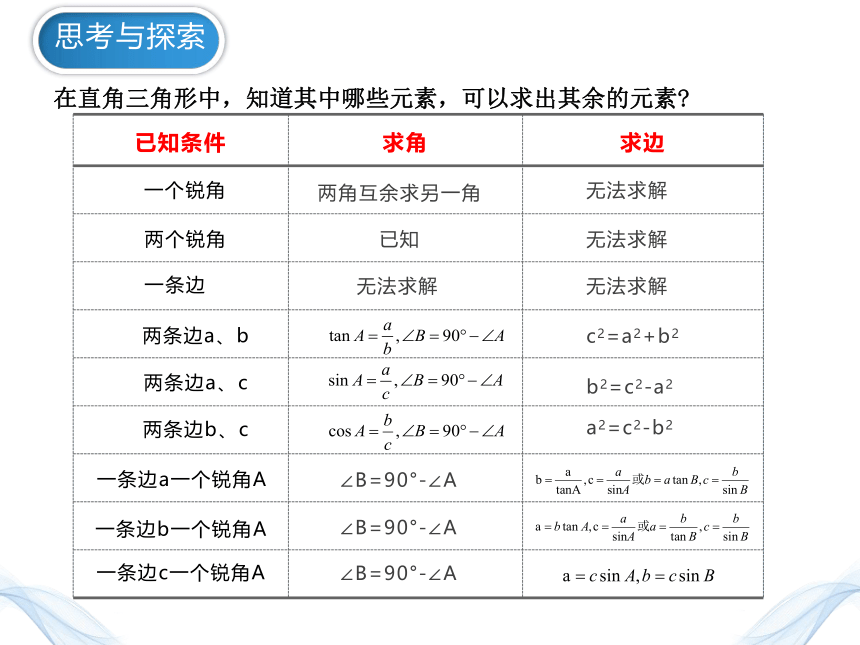
思考与探索
在直角三角形中,知道其中哪些元素,可以求出其余的元素
已知条件 求角 求边
一个锐角
两个锐角
一条边
两条边a、b
两条边a、c
两条边b、c
一条边a一个锐角A
一条边b一个锐角A
一条边c一个锐角A
两角互余求另一角
已知
无法求解
无法求解
无法求解
无法求解
∠B=90°-∠A
∠B=90°-∠A
∠B=90°-∠A
c2=a2+b2
b2=c2-a2
a2=c2-b2
新课探究
在直角三角形中除直角外,由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
解直角三角形:
要求出直角三角形的其他元素,需要的条件分为两种情况:
(1)已知两条边,求第三条边和两个锐角;
(2)已知一条边和一个锐角,求另外两条边和另一个锐角.
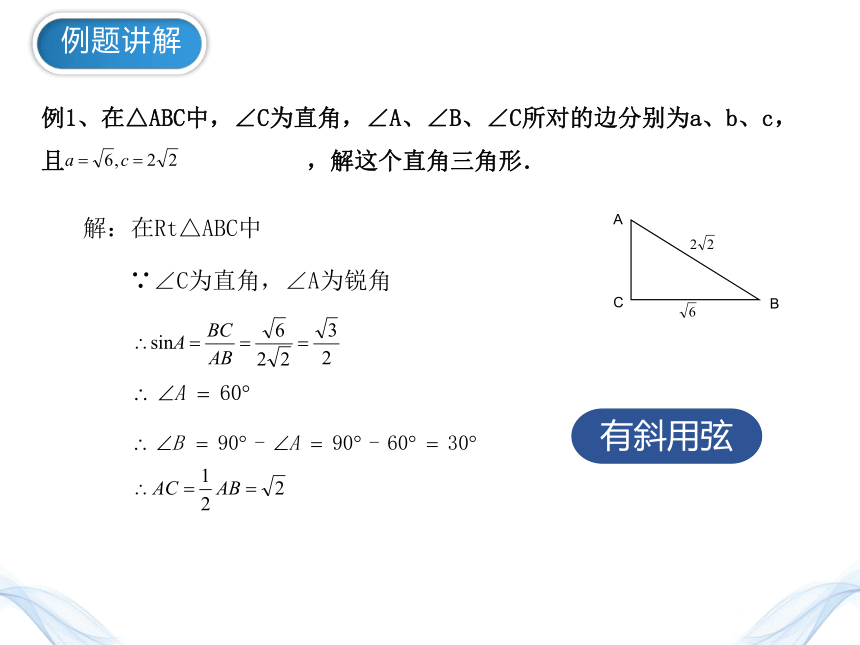
例题讲解
例1、在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且 ,解这个直角三角形.
解:在Rt△ABC中
∵∠C为直角,∠A为锐角
A
B
C
有斜用弦
例题讲解
例2、在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且b=20,∠B=35°,解这个三角形(精确到0.1).
解:在Rt△ABC中
无斜用切
取原避中
基础练习
在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,根据已知条件,解直角三角形.
(1)c=8,∠A=60°
(2)b= ,c=4
答案:a= ,b=4,∠B=30°
答案:a= ,∠A=45°,∠B=45°
拓展提高
例3、在△ABC中,∠A=60°,∠B=45°,BC=2,求AB,AC的长.
解:过点C作CD⊥AB,垂足为D
在Rt△BCD中
∵∠B=45°,BC=2
在Rt△ACD中
D
提高练习
在Rt△ABC中,∠C=90°,AC=6,∠A的平分线AD= ,求AB,BC的长.
答案:AB=12,BC=
提示
求解非直角三角形的边角问题,常通过添加适当的辅助线,将其转换为直角三角形来解.
C
A
B
D
A
B
C
E
D
课堂小结
注意事项
解三角形
解直角三角形
所需条件
在直角三角形中除直角外,由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
(1)已知两条边
(2)已知一条边和一个锐角
有斜用弦
无斜用切
取原避中
构造直角三角形,非直角转化为直角
布置作业
1、在Rt△ABC中,∠C=90°,若∠A=30°则∠B= ,
若∠A=30°,a=1 ,则b= ,c= 。
2、根据下列条件解直角三角形,在Rt△ABC中,∠C=90°,
a、b、c分别为∠A、∠B,∠C的对边:
(1) b= , c=4
(2)∠A=45°,a=
3、在△ABC中,∠A=30°,∠B=45°,AC=4,求BC、AB.
提高练习
在△ABC中,D为BC边上的一点,BD=6,AD=14,CD=12,△ACD的面积是 ,求AB的长.
谢谢观看!
28.2.1解直角三角形
新人教版九年级下册
知识回顾
1、一个直角三角形有几个元素?
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90°
(3)边角之间的关系:
A
C
B
a
b
c
有3条边和3个角,其中有一个角为直角
2、它们之间有何关系?
思考与探索
在直角三角形中,知道其中哪些元素,可以求出其余的元素
已知条件 求角 求边
一个锐角
两个锐角
一条边
两条边a、b
两条边a、c
两条边b、c
一条边a一个锐角A
一条边b一个锐角A
一条边c一个锐角A
两角互余求另一角
已知
无法求解
无法求解
无法求解
无法求解
∠B=90°-∠A
∠B=90°-∠A
∠B=90°-∠A
c2=a2+b2
b2=c2-a2
a2=c2-b2
新课探究
在直角三角形中除直角外,由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
解直角三角形:
要求出直角三角形的其他元素,需要的条件分为两种情况:
(1)已知两条边,求第三条边和两个锐角;
(2)已知一条边和一个锐角,求另外两条边和另一个锐角.
例题讲解
例1、在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且 ,解这个直角三角形.
解:在Rt△ABC中
∵∠C为直角,∠A为锐角
A
B
C
有斜用弦
例题讲解
例2、在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且b=20,∠B=35°,解这个三角形(精确到0.1).
解:在Rt△ABC中
无斜用切
取原避中
基础练习
在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,根据已知条件,解直角三角形.
(1)c=8,∠A=60°
(2)b= ,c=4
答案:a= ,b=4,∠B=30°
答案:a= ,∠A=45°,∠B=45°
拓展提高
例3、在△ABC中,∠A=60°,∠B=45°,BC=2,求AB,AC的长.
解:过点C作CD⊥AB,垂足为D
在Rt△BCD中
∵∠B=45°,BC=2
在Rt△ACD中
D
提高练习
在Rt△ABC中,∠C=90°,AC=6,∠A的平分线AD= ,求AB,BC的长.
答案:AB=12,BC=
提示
求解非直角三角形的边角问题,常通过添加适当的辅助线,将其转换为直角三角形来解.
C
A
B
D
A
B
C
E
D
课堂小结
注意事项
解三角形
解直角三角形
所需条件
在直角三角形中除直角外,由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
(1)已知两条边
(2)已知一条边和一个锐角
有斜用弦
无斜用切
取原避中
构造直角三角形,非直角转化为直角
布置作业
1、在Rt△ABC中,∠C=90°,若∠A=30°则∠B= ,
若∠A=30°,a=1 ,则b= ,c= 。
2、根据下列条件解直角三角形,在Rt△ABC中,∠C=90°,
a、b、c分别为∠A、∠B,∠C的对边:
(1) b= , c=4
(2)∠A=45°,a=
3、在△ABC中,∠A=30°,∠B=45°,AC=4,求BC、AB.
提高练习
在△ABC中,D为BC边上的一点,BD=6,AD=14,CD=12,△ACD的面积是 ,求AB的长.
谢谢观看!
