华东师大版七年级下册数学 10.3.2旋转的特征 课件(共17张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 10.3.2旋转的特征 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 484.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 09:05:25 | ||
图片预览






文档简介
(共17张PPT)
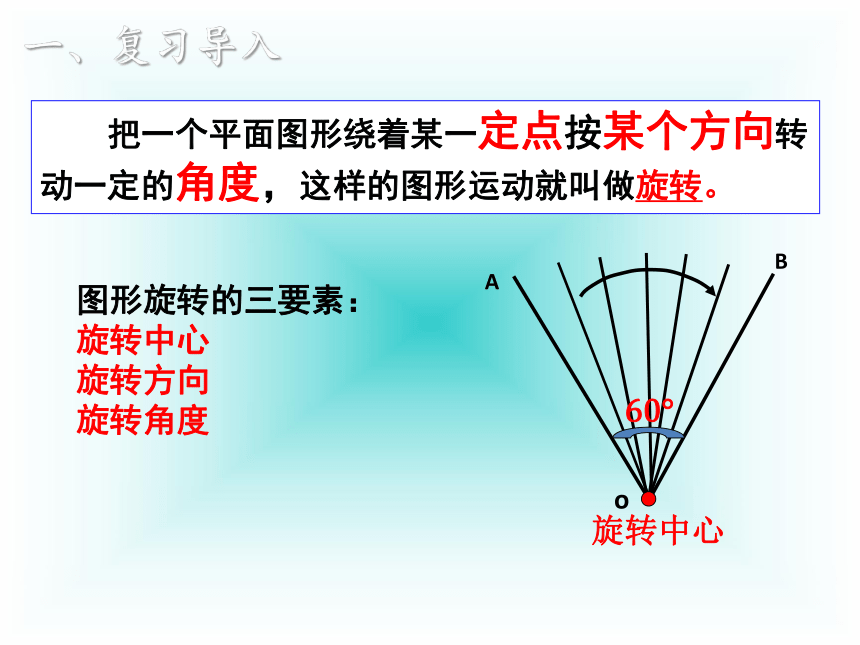
10.3.2旋转的特征
60°
旋转中心
A
o
B
图形旋转的三要素:
旋转中心
旋转方向
旋转角度
1、什么是图形的旋转?图形的旋转是由什么决定的?
一、复习导入
把一个平面图形绕着某一定点按某个方向转动一定的角度,这样的图形运动就叫做旋转。
旋转角是________________;
旋转角的度数是_________;
点B的对应点是________;
线段OB的对应线段是________;
∠A的对应角是________;
旋转中心是________;
旋转方向是_________________;
2、如图,△AOB绕点O旋转得到△ A′OB′,则:
点B′
线段OB′
∠A′
点O
∠AOA′
﹑∠BOB′
逆时针
45°
一、复习导入
二、任务驱动,分步探究
观察第119页图10.3.4和120页图10.3.5,你能发现有哪些线
段相等,有哪些角相等?完成122页的填空。
思考:我们从以下几个方面思考图形旋转前后的变化。
1、图形上每一点的旋转方向是否相同?
2、图形上每一点的旋转角度是否相同?
3、对应点到旋转中心的距离有什么关系?
4、对应线段的关系?
5、对应角的关系?
6、图形的大小和形状是
否发生变化?
图10.3.4
图10.3.5
演示
探究点一:旋转的特征
A
O
B
A′
B′
45°
图(1)
如图(1),线段OA、OB都是绕点O逆时针
旋转45°到对应线段OA′、OB′,而且
OA=____ OB=______ AB=_____;
∠AOB=_________ ∠A=_____ ∠B=______.
OA′
OB′
A′B′
∠ A′OB′
∠ A′
B′
探究点一:旋转的特征
如图(2),旋转中心是点O,点A、B、C都是绕点O逆时针旋转60°到对应点A′、B′、C′,
而且OA=____,OB=____,OC=____;
AB=____,BC=_____,AC=______.
∠CAB=________ ∠ABC=________ ∠BCA=________.
O
60°
A
B
C
A′
C′
B′
图(2)
OA′
OB′
OC′
A′B′
B′C′
A′C′
∠ C′A′B′
∠ A′ B′ C′
∠ B′ C′ A′
于是我们可以得到图形旋转的特征:
1、图形中的每一个点都绕着旋转中心按同 一个旋转方向旋转了同样大小的角度。
2、对应点到旋转中心的距离相等。
3、对应线段相等、对应角相等。
探究点一:旋转的特征
4、图形的形状与大小不变。
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
B
A
C
O
D
E
F
例题分析
如图,点D是等边△ABC内一点, 若将△ABD
点A
A
B
C
D
旋转到△ACP, 则旋转中心是 ; 旋转角是
= 度;
∠BAC
60
则△ADP是 三角形.
等边
P
若连结DP,
例题分析
前面我们学习10.1.4设计轴对称图案时,利用轴对称,我们可以设计出许多漂亮的图案。其实,利用旋转,我们也可以设计出漂亮的图案,如图,香港特别行政区区旗中央的紫荆花图案就是利用旋转设计的,它是由其中一个花瓣经过几次旋转得到的 每次旋转了多少度?
每次旋转720。
探究二:旋转作图
解:经过4次旋转得到的,
一个简单的图形经过几次旋转就能变成漂亮的图案,那么如何画出旋转后的图形呢?试画出 ABC绕点O逆时针旋转90°后的图形。
O
A
B
C
·
A′
B′
C′
90°
画法
(1)连结OA、OB、OC;
(2)分别画OA、OB、OC绕点O
逆时针旋转90°的线段OA′、
O B′、O C′;
(3)连接A′B′,A′C′,B′C′
则△A′B′C′就是所求的旋转图形。
探究二:旋转作图
三、欣赏旋转在现实生活中的应用
1.如图,△ABO绕点O旋转得到△CDO,在这个旋转过程中:
(1)旋转中心是_____,旋转角是_______________;
(2)经过旋转,点A、B分别移到了__________;
(3)若AO=3cm,则CO=__________;
A
B
C
D
O
点O
∠AOC或∠BOD
点C、D
3cm
55°
85°
55°
25°
(4)若∠AOC=55°,∠AOD=25°,则∠BOD=___,∠BOC=___.
练习
2.如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋 转后到达△CAE的位置。问:
(1)旋转中心是_____,旋转的度数是____.
(2)若∠DCB=20°,则∠CDB=___,∠AEC=___, ∠BAE=___.
(3)如果连结DE,那么△DCE是________三角形。
点C
90°
115°
90°
等腰直角
115°
A
E
C
B
D
20°
练习
四、课堂小结
1、旋转有哪些特征?
2、你会找图形旋转前后的对应元素了吗?
图形中的每一个点都绕着旋转中心按同一个旋转方向旋转了同样大小的角度。
对应点到旋转中心的距离相等。
对应线段相等、对应角相等。
图形的形状与大小不变。
五、作业:拓广探索
如图:△ABD、△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的知识说明上述关系成立的理由吗?
3.在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案。
A
B
C
O
A
B
C
┓
┓
D
F
10.3.2旋转的特征
60°
旋转中心
A
o
B
图形旋转的三要素:
旋转中心
旋转方向
旋转角度
1、什么是图形的旋转?图形的旋转是由什么决定的?
一、复习导入
把一个平面图形绕着某一定点按某个方向转动一定的角度,这样的图形运动就叫做旋转。
旋转角是________________;
旋转角的度数是_________;
点B的对应点是________;
线段OB的对应线段是________;
∠A的对应角是________;
旋转中心是________;
旋转方向是_________________;
2、如图,△AOB绕点O旋转得到△ A′OB′,则:
点B′
线段OB′
∠A′
点O
∠AOA′
﹑∠BOB′
逆时针
45°
一、复习导入
二、任务驱动,分步探究
观察第119页图10.3.4和120页图10.3.5,你能发现有哪些线
段相等,有哪些角相等?完成122页的填空。
思考:我们从以下几个方面思考图形旋转前后的变化。
1、图形上每一点的旋转方向是否相同?
2、图形上每一点的旋转角度是否相同?
3、对应点到旋转中心的距离有什么关系?
4、对应线段的关系?
5、对应角的关系?
6、图形的大小和形状是
否发生变化?
图10.3.4
图10.3.5
演示
探究点一:旋转的特征
A
O
B
A′
B′
45°
图(1)
如图(1),线段OA、OB都是绕点O逆时针
旋转45°到对应线段OA′、OB′,而且
OA=____ OB=______ AB=_____;
∠AOB=_________ ∠A=_____ ∠B=______.
OA′
OB′
A′B′
∠ A′OB′
∠ A′
B′
探究点一:旋转的特征
如图(2),旋转中心是点O,点A、B、C都是绕点O逆时针旋转60°到对应点A′、B′、C′,
而且OA=____,OB=____,OC=____;
AB=____,BC=_____,AC=______.
∠CAB=________ ∠ABC=________ ∠BCA=________.
O
60°
A
B
C
A′
C′
B′
图(2)
OA′
OB′
OC′
A′B′
B′C′
A′C′
∠ C′A′B′
∠ A′ B′ C′
∠ B′ C′ A′
于是我们可以得到图形旋转的特征:
1、图形中的每一个点都绕着旋转中心按同 一个旋转方向旋转了同样大小的角度。
2、对应点到旋转中心的距离相等。
3、对应线段相等、对应角相等。
探究点一:旋转的特征
4、图形的形状与大小不变。
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
B
A
C
O
D
E
F
例题分析
如图,点D是等边△ABC内一点, 若将△ABD
点A
A
B
C
D
旋转到△ACP, 则旋转中心是 ; 旋转角是
= 度;
∠BAC
60
则△ADP是 三角形.
等边
P
若连结DP,
例题分析
前面我们学习10.1.4设计轴对称图案时,利用轴对称,我们可以设计出许多漂亮的图案。其实,利用旋转,我们也可以设计出漂亮的图案,如图,香港特别行政区区旗中央的紫荆花图案就是利用旋转设计的,它是由其中一个花瓣经过几次旋转得到的 每次旋转了多少度?
每次旋转720。
探究二:旋转作图
解:经过4次旋转得到的,
一个简单的图形经过几次旋转就能变成漂亮的图案,那么如何画出旋转后的图形呢?试画出 ABC绕点O逆时针旋转90°后的图形。
O
A
B
C
·
A′
B′
C′
90°
画法
(1)连结OA、OB、OC;
(2)分别画OA、OB、OC绕点O
逆时针旋转90°的线段OA′、
O B′、O C′;
(3)连接A′B′,A′C′,B′C′
则△A′B′C′就是所求的旋转图形。
探究二:旋转作图
三、欣赏旋转在现实生活中的应用
1.如图,△ABO绕点O旋转得到△CDO,在这个旋转过程中:
(1)旋转中心是_____,旋转角是_______________;
(2)经过旋转,点A、B分别移到了__________;
(3)若AO=3cm,则CO=__________;
A
B
C
D
O
点O
∠AOC或∠BOD
点C、D
3cm
55°
85°
55°
25°
(4)若∠AOC=55°,∠AOD=25°,则∠BOD=___,∠BOC=___.
练习
2.如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋 转后到达△CAE的位置。问:
(1)旋转中心是_____,旋转的度数是____.
(2)若∠DCB=20°,则∠CDB=___,∠AEC=___, ∠BAE=___.
(3)如果连结DE,那么△DCE是________三角形。
点C
90°
115°
90°
等腰直角
115°
A
E
C
B
D
20°
练习
四、课堂小结
1、旋转有哪些特征?
2、你会找图形旋转前后的对应元素了吗?
图形中的每一个点都绕着旋转中心按同一个旋转方向旋转了同样大小的角度。
对应点到旋转中心的距离相等。
对应线段相等、对应角相等。
图形的形状与大小不变。
五、作业:拓广探索
如图:△ABD、△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的知识说明上述关系成立的理由吗?
3.在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案。
A
B
C
O
A
B
C
┓
┓
D
F
