华东师大版七年级下册数学 8.2.2 不等式的简单变形 课件(共16张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 8.2.2 不等式的简单变形 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 295.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 11:09:55 | ||
图片预览






文档简介
(共16张PPT)
不等式的简单变形
引入新课
提问:在解一元一次方程时,我们主要是对方程进行变形。那么方程变形的依据是什么?
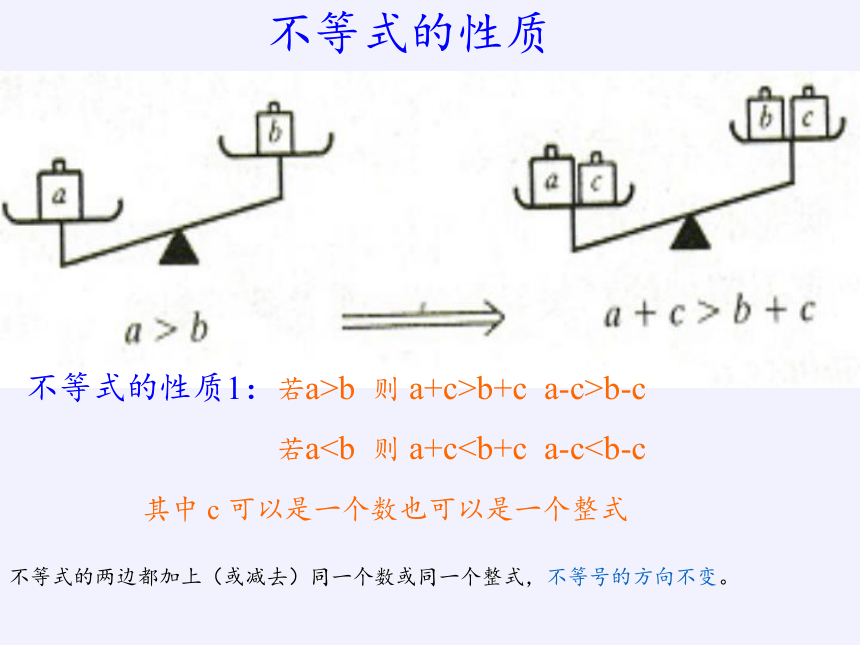
不等式的性质
不等式的性质1:若a>b 则 a+c>b+c a-c>b-c
若a其中 c 可以是一个数也可以是一个整式
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
>
>
>
>
练习:已知 a > b,用不等号填空。
① a + 2 b + 2 ② a - 3 b - 3
③ a + b b + b ④ a +b 2b
不等式的性质2:若a>b, 并且 c>0 则 ac>bc a/c>b/c
若a0 则 ac不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
>
>
练习:已知 a > b,用不等号填空
2a 2b (2) a b
(3) 7a 7b (4) 3a 3b
>
>
探索:将不等式7>4两边都乘以同一数,比较所得的数的大小,用“>”或 “<”填空:
7ⅹ3 4ⅹ3 7ⅹ1 4ⅹ1 7ⅹ2 4ⅹ2
7ⅹ0 4ⅹ0 7ⅹ(-1) 4ⅹ(-1)
7ⅹ(-2) 4ⅹ(-2) 7ⅹ(-3) 4ⅹ(-3)
从中你发现了什么?
不等式的性质3:若a>b, 并且 c<0 则 ac若abc a/c>b/c
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
探索:探索:将不等式7>4两边都乘以同一数,比较所得的数的大小,用“>”或 “<”填空:
7ⅹ3 4ⅹ3 7ⅹ1 4ⅹ1 7ⅹ2 4ⅹ2
7ⅹ0 4ⅹ0 7ⅹ(-1) 4ⅹ(-1)
7ⅹ(-2) 4ⅹ(-2) 7ⅹ(-3) 4ⅹ(-3)
从中你发现了什么?
练习:已知 a > b,用不等号填空。
-2a -2b (2) - 7a - 7b
(3) - a - b (4) 4 - a 4- b
<
<
<
<
例题1. 解不等式:
(1) x-7 < 8 (2) 3x < 2x-3
解:(1)不等式的两边都加上7,不等号方向不变
所以 x - 7 + 7 < 8 + 7
x < 15
(2)不等式的两边都减去2x,不等号方向不变
所以 3x - 2x < 2x – 3 - 2x
x < -3
例题2. 解不等式:
x >-3 (2)–2x < 6 (3) 2x < -6
(1) x > -3
x > -6
2 × x > -3×2
解:不等式的两边都乘以 2(或除以 ),不等号的方向不变
(2) –2x < 6
(3) 2x < -6
解:不等式的两边都除以(-2),不等号的方向改变
解:不等式的两边都除以 2 ,不等号的方向不变
–2x ÷(-2) > 6 ÷(-2)
2x ÷ 2 < -6 ÷ 2
x > -3
x < -3
(1) –1 < -2x
解:不等式的两边都除以(-2),不等号的方向改变
-1 ÷(-2)> -2x ÷ (-2)
练习: 解不等式:
(1) –1 < -2x (2) - - x >
(3) 3x+4 ≥ 7x
> x
即 x <
(2) – x >
解:不等式的两边都乘以(- ),不等号的方向改变
(- )×( – x )< (- )×
所以 x < -
9
4
(3) 3x+4 ≥ 7x
解:移项得 3x-7x ≥ -4
-4x ≥ -4
不等式的两边都除以(-4),不等号的方向改变
-4x ÷(-4) ≤ -4 ÷(-4)
所以 x ≤ 1
3. 方程与不等式性质的异同。
1. 不等式的三个性质。
2. 不等式性质3中不等号的变号问题。
本节课你学到了什么
不等式的基本性质
方程的基本性质
相同处
相同处
不同处
方程两边都乘以(或除以)同一个负数,方程仍成立
不等式与方程的性质比较
方程两边加上(减去)同一个数成同一个整式,方程仍成立
方程两边都乘以(或除以)同一个正数,方程仍成立
不等式的两边加上(或减去)同一个数或同一个整式,不等号的方向不变
个正数不等式的两边都乘以(或除以)同一,不等号的方向不变
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变
再 见
谢 谢
不等式的简单变形
引入新课
提问:在解一元一次方程时,我们主要是对方程进行变形。那么方程变形的依据是什么?
不等式的性质
不等式的性质1:若a>b 则 a+c>b+c a-c>b-c
若a其中 c 可以是一个数也可以是一个整式
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
>
>
>
>
练习:已知 a > b,用不等号填空。
① a + 2 b + 2 ② a - 3 b - 3
③ a + b b + b ④ a +b 2b
不等式的性质2:若a>b, 并且 c>0 则 ac>bc a/c>b/c
若a
>
>
练习:已知 a > b,用不等号填空
2a 2b (2) a b
(3) 7a 7b (4) 3a 3b
>
>
探索:将不等式7>4两边都乘以同一数,比较所得的数的大小,用“>”或 “<”填空:
7ⅹ3 4ⅹ3 7ⅹ1 4ⅹ1 7ⅹ2 4ⅹ2
7ⅹ0 4ⅹ0 7ⅹ(-1) 4ⅹ(-1)
7ⅹ(-2) 4ⅹ(-2) 7ⅹ(-3) 4ⅹ(-3)
从中你发现了什么?
不等式的性质3:若a>b, 并且 c<0 则 ac
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
探索:探索:将不等式7>4两边都乘以同一数,比较所得的数的大小,用“>”或 “<”填空:
7ⅹ3 4ⅹ3 7ⅹ1 4ⅹ1 7ⅹ2 4ⅹ2
7ⅹ0 4ⅹ0 7ⅹ(-1) 4ⅹ(-1)
7ⅹ(-2) 4ⅹ(-2) 7ⅹ(-3) 4ⅹ(-3)
从中你发现了什么?
练习:已知 a > b,用不等号填空。
-2a -2b (2) - 7a - 7b
(3) - a - b (4) 4 - a 4- b
<
<
<
<
例题1. 解不等式:
(1) x-7 < 8 (2) 3x < 2x-3
解:(1)不等式的两边都加上7,不等号方向不变
所以 x - 7 + 7 < 8 + 7
x < 15
(2)不等式的两边都减去2x,不等号方向不变
所以 3x - 2x < 2x – 3 - 2x
x < -3
例题2. 解不等式:
x >-3 (2)–2x < 6 (3) 2x < -6
(1) x > -3
x > -6
2 × x > -3×2
解:不等式的两边都乘以 2(或除以 ),不等号的方向不变
(2) –2x < 6
(3) 2x < -6
解:不等式的两边都除以(-2),不等号的方向改变
解:不等式的两边都除以 2 ,不等号的方向不变
–2x ÷(-2) > 6 ÷(-2)
2x ÷ 2 < -6 ÷ 2
x > -3
x < -3
(1) –1 < -2x
解:不等式的两边都除以(-2),不等号的方向改变
-1 ÷(-2)> -2x ÷ (-2)
练习: 解不等式:
(1) –1 < -2x (2) - - x >
(3) 3x+4 ≥ 7x
> x
即 x <
(2) – x >
解:不等式的两边都乘以(- ),不等号的方向改变
(- )×( – x )< (- )×
所以 x < -
9
4
(3) 3x+4 ≥ 7x
解:移项得 3x-7x ≥ -4
-4x ≥ -4
不等式的两边都除以(-4),不等号的方向改变
-4x ÷(-4) ≤ -4 ÷(-4)
所以 x ≤ 1
3. 方程与不等式性质的异同。
1. 不等式的三个性质。
2. 不等式性质3中不等号的变号问题。
本节课你学到了什么
不等式的基本性质
方程的基本性质
相同处
相同处
不同处
方程两边都乘以(或除以)同一个负数,方程仍成立
不等式与方程的性质比较
方程两边加上(减去)同一个数成同一个整式,方程仍成立
方程两边都乘以(或除以)同一个正数,方程仍成立
不等式的两边加上(或减去)同一个数或同一个整式,不等号的方向不变
个正数不等式的两边都乘以(或除以)同一,不等号的方向不变
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变
再 见
谢 谢
