华东师大版八年级下册数学 20.2.1 中位数和众数 课件 (共28张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 20.2.1 中位数和众数 课件 (共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 412.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 20:55:57 | ||
图片预览








文档简介
(共28张PPT)
中位数和众数
招 聘 启 事
因本广告公司扩大规模,现需招员工若干名,我公司员工人均月收入为3800元,有意者欢迎加盟!
XX广告公司人事部
2015年7月20日
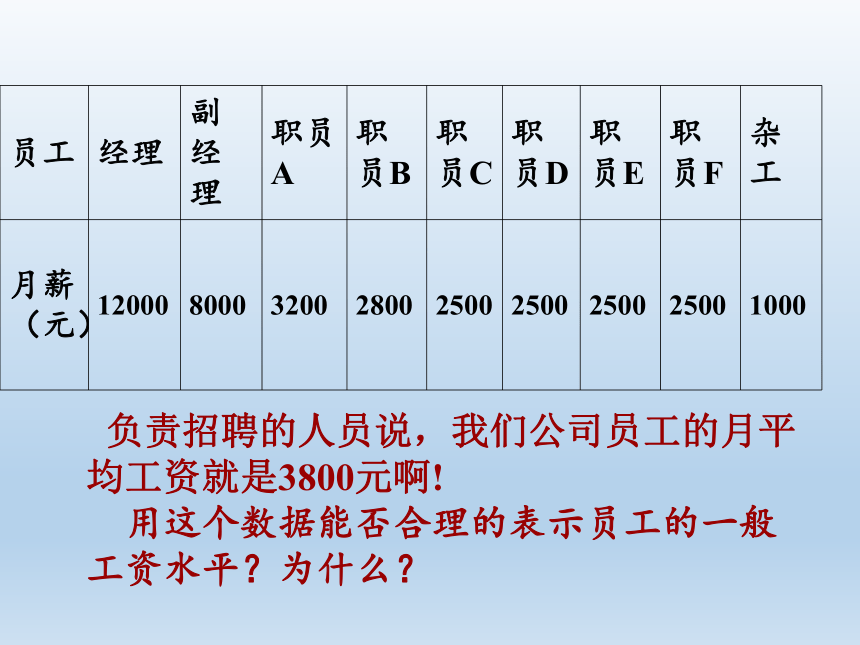
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工
月薪(元) 12000 8000 3200 2800 2500 2500 2500 2500 1000
负责招聘的人员说,我们公司员工的月平均工资就是3800元啊!
用这个数据能否合理的表示员工的一般工资水平?为什么?
学习目标
1.理解中位数和众数的概念及意义,会求出一组数据的中位数和众数。
2.通过实际问题情境探索中位数和众数的意义,培养观察能力和数据处理能力。
3.通过实例经历用中位数、众数分析数据,感受统计在生活中的应用。
1、 请同学们阅读课本P140-141问题1理解什么是中位数,并总结求一组数据中位数的方法.
将一组数据按照从小到大的顺序排列后,处在正中间位置的一个数(正中间位置两个数的平均数),就是这组数据的中位数.
阅读检测:
1. 求下列数据的中位数吗?
(1) 4, 7, 2, 5, 6, 3
(2) 3, 5, 4, 8, 2,9, 10.
解:(1)从小到大排列为: 2, 3, 4, 5, 6, 7.处在正中间位置的两个数是4和5, 所以中位数是
(2)从小到大排列为2,3,4,5,8,9,10,正中间的数是5,所以中位数是5.
合作探究
我们八(4)班41名同学中,13岁的有1人,14岁的有22人,15岁的有16人,16岁的有2人,则我们班同学年龄的中位数是 。
变为:我校八(8)40名同学中,13岁的有1人,14岁的有21人,15岁的有16人,16岁的有2人,则(8)同学年龄的中位数是 。
求中位数的一般步骤:
1、排序;
2、若奇数个数,取正中间位置的一个数.
若有偶数个数,位于正中间的两个数的平均数.
一组数据有n个数,你知道中间位置如何确定吗
n 为奇数时,中间位置是第 个
n为偶数时,中间位置是第 , 个
合作攻关
阅读课本P142,理解什么是众数,并说明如何求一组数据的众数。
(3) 众数:
如下表,统计每一气温在31个城市预报最高气温数据中出现的频数,可以找出频数最多的那个气温值,它就是众数
气温℃ 9 16 17 18 19 20 21 22 23 24 25 26 27 29 30
频数 1 1 2 2 1 5 4 4 3 1 1 2 1 1 2
由表可知,这些城市当日预报最高气温的众数是20℃.
思考:若20℃和22℃频数并列最多,都是5,那么众数是多少
总结:
一组数据中出现频数(次
数)最多的那个数,就是这
组数据的众数。
求下列各组数据的众数:
(1)20, 20, 22, 21, 22, 22.
(2) 5,2,7,3,5,3,6,3,5,
(3)21,35,27,65,9.
注意:一组数据众数的情况:
(1)可能只有一个
(2)可能一个都没有
(3)可能有多个
试一试
解:(1)22出现了3次,是这组数据中频数最多的,所以这组数据的众数是22.
3.我们学校对八年级100名同学所穿秋季校服的尺码进行统计,统计结果如下表:
尺码(cm) 145 150 155 160 165 170 175 180
人数 1 4 8 13 20 26 23 5
这100名学生校服尺码的中位数和众数分别是多少?
中位数:170cm,众数:170cm
试一试
平均数
中位数
众 数
---平均水平
---中等水平
---多数水平
关键词
平均数、中位数和众数从不同的侧面描述了一组数据的集中趋势,正因为如此,这三个指标常被用来作为一组数据的代表.
1、 判断题: (正确的打“√”,不正确的打“×”)
(1) 给定一组数据,那么这组数据的平均数一定只有一个. ( )
(2) 给定一组数据,那么这组数据的中位数一定只有一个. ( )
(3) 给定一组数据,那么这组数据的众数一定只有一个. ( )
(4) 给定一组数据,那么这组数据的平均数一定位于最大值和最小值之间.( )
(6) 给定一组数据,如果找不到众数,那么众数一定就是0.( )
试一试
(5) 给定一组数据,那么这组数据的中位数一定等于最小值和最大值的算术平均数.( )
(1)、元旦要组织一次座谈会,准备水果时应关注的是学生喜欢所吃水果数据的代表( )
A、平均数 B、中位数 C、众数
(2)、解放路学校八(4)班有42人,八(5)班有43人,要比较两个班的平均成绩,应选择哪个数据的代表( )
A、平均数 B、中位数 C、众数
(3)、在学校组织的卡拉OK比赛中,你想知道自己在所有选手中处于什么水平,应该选择哪个数据的代表( )
A、平均数 B、中位数 C、众数
C
A
B
试一试
2、选择
3、 我们4班的教室里,三位同学正在为谁的数学成绩最好而争论,他们的5次数学成绩分别为:
昊华:62, 94, 95, 98, 98;
康伟:62,62,98, 99, 100;
郭良:40, 62,85, 99,99.
他们都认为自己的成绩比另两位同学的好,你能讲出他们认为好的理由吗
活学活用
……
1、知道了什么是中位数和众数。
2、会求一组数据的中位数和众数,
3、求中位数时一定要先排序,而且总数奇、偶时有所不同。
4、 平均数、中位数和众数从不同的侧面描述了一组数据的集中趋势。
……
本节课我收获了
1. 课本习题20.2 第1,2题。
2. 收集本班同学体重数据 ,并求出本班学生体重的的平均数、中位数、
众数.
一个成功的竞争者应该经得起风雨,
应该具有抗挫折的能力。
教师寄语
4、从甲、乙、丙三个厂家生产的产品冰箱分别随机抽取10台,对其使用寿命跟踪调查,结果如下:
(单位:年)
甲:6,7,8,12,10,10,12,9,10,10,
乙:8,9,8,9,10,12,11,11,10,12;
丙:7,7,8,8,9,11,11,12,12,13;
三个厂家在广告中都称该产品的使用寿命是10年。
你能用所学的知识来解释使用寿命为什么都是10年吗
厂家在广告中分别运用了平均数、众数、中位数
的哪一种特征数:甲 ,乙 ,
丙 .
众数
平均数
中位数
试一试
问题情景:据中国气象局2011年10月20日19时30预报,
2011年10月20日预报21的各地最高气温(℃)
北京 17 天津 22 石家庄 21 太原 21 呼和浩特 18 沈阳 22 长春 20 哈尔滨
19
上海 23 南京 23 杭州 24 合肥 22 福州 27 南昌 26 济南 23 郑州
22
武汉 25 长沙 26 广州 30 海口 30 南宁 29 成都 21 重庆 20 贵阳
17
昆明 20 拉萨 20 西安 21 兰州 18 银川 20 西宁 16 乌鲁木齐 9
求一组数据的中位数的方法:
1.排序(从小到大或从大到小)
2.正中间一个数(或正中间两个数的平
均数)
注意:
1、奇数个数据、偶数个数据求中位数时有区别
2、每一组数据都有中位数
平均数 中位数 众数
不 同 点 是否存在 存在 存在 可有可无
个数 1 1 没有、1个或多个
受极值影响 受 不受 不受
数据特征 平均水平 中等水平 多数水平
确定方法 公式 排序 计数
共同点 都是描述一组数据的集中趋势 平均数是概括一组数据的一种常用指标,反映了这组数据中各数据的平均大小.
中位数是概括一组数据的另一种指标,如果将一组数据按由小到大的顺序排列(即使有相等的数据也要全部参加排列),那么中位数的左边和右边恰有一样多的数据.
众数告诉我们,这个值出现的次数最多.一组数据可以有不止一个众数,也可能没有众数.
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工
月薪(元) 12000 8000 3200 2800 2500 2500 2500 2500 1000
你能用本节课所学的知识来分析这组数据吗
谢 谢
中位数和众数
招 聘 启 事
因本广告公司扩大规模,现需招员工若干名,我公司员工人均月收入为3800元,有意者欢迎加盟!
XX广告公司人事部
2015年7月20日
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工
月薪(元) 12000 8000 3200 2800 2500 2500 2500 2500 1000
负责招聘的人员说,我们公司员工的月平均工资就是3800元啊!
用这个数据能否合理的表示员工的一般工资水平?为什么?
学习目标
1.理解中位数和众数的概念及意义,会求出一组数据的中位数和众数。
2.通过实际问题情境探索中位数和众数的意义,培养观察能力和数据处理能力。
3.通过实例经历用中位数、众数分析数据,感受统计在生活中的应用。
1、 请同学们阅读课本P140-141问题1理解什么是中位数,并总结求一组数据中位数的方法.
将一组数据按照从小到大的顺序排列后,处在正中间位置的一个数(正中间位置两个数的平均数),就是这组数据的中位数.
阅读检测:
1. 求下列数据的中位数吗?
(1) 4, 7, 2, 5, 6, 3
(2) 3, 5, 4, 8, 2,9, 10.
解:(1)从小到大排列为: 2, 3, 4, 5, 6, 7.处在正中间位置的两个数是4和5, 所以中位数是
(2)从小到大排列为2,3,4,5,8,9,10,正中间的数是5,所以中位数是5.
合作探究
我们八(4)班41名同学中,13岁的有1人,14岁的有22人,15岁的有16人,16岁的有2人,则我们班同学年龄的中位数是 。
变为:我校八(8)40名同学中,13岁的有1人,14岁的有21人,15岁的有16人,16岁的有2人,则(8)同学年龄的中位数是 。
求中位数的一般步骤:
1、排序;
2、若奇数个数,取正中间位置的一个数.
若有偶数个数,位于正中间的两个数的平均数.
一组数据有n个数,你知道中间位置如何确定吗
n 为奇数时,中间位置是第 个
n为偶数时,中间位置是第 , 个
合作攻关
阅读课本P142,理解什么是众数,并说明如何求一组数据的众数。
(3) 众数:
如下表,统计每一气温在31个城市预报最高气温数据中出现的频数,可以找出频数最多的那个气温值,它就是众数
气温℃ 9 16 17 18 19 20 21 22 23 24 25 26 27 29 30
频数 1 1 2 2 1 5 4 4 3 1 1 2 1 1 2
由表可知,这些城市当日预报最高气温的众数是20℃.
思考:若20℃和22℃频数并列最多,都是5,那么众数是多少
总结:
一组数据中出现频数(次
数)最多的那个数,就是这
组数据的众数。
求下列各组数据的众数:
(1)20, 20, 22, 21, 22, 22.
(2) 5,2,7,3,5,3,6,3,5,
(3)21,35,27,65,9.
注意:一组数据众数的情况:
(1)可能只有一个
(2)可能一个都没有
(3)可能有多个
试一试
解:(1)22出现了3次,是这组数据中频数最多的,所以这组数据的众数是22.
3.我们学校对八年级100名同学所穿秋季校服的尺码进行统计,统计结果如下表:
尺码(cm) 145 150 155 160 165 170 175 180
人数 1 4 8 13 20 26 23 5
这100名学生校服尺码的中位数和众数分别是多少?
中位数:170cm,众数:170cm
试一试
平均数
中位数
众 数
---平均水平
---中等水平
---多数水平
关键词
平均数、中位数和众数从不同的侧面描述了一组数据的集中趋势,正因为如此,这三个指标常被用来作为一组数据的代表.
1、 判断题: (正确的打“√”,不正确的打“×”)
(1) 给定一组数据,那么这组数据的平均数一定只有一个. ( )
(2) 给定一组数据,那么这组数据的中位数一定只有一个. ( )
(3) 给定一组数据,那么这组数据的众数一定只有一个. ( )
(4) 给定一组数据,那么这组数据的平均数一定位于最大值和最小值之间.( )
(6) 给定一组数据,如果找不到众数,那么众数一定就是0.( )
试一试
(5) 给定一组数据,那么这组数据的中位数一定等于最小值和最大值的算术平均数.( )
(1)、元旦要组织一次座谈会,准备水果时应关注的是学生喜欢所吃水果数据的代表( )
A、平均数 B、中位数 C、众数
(2)、解放路学校八(4)班有42人,八(5)班有43人,要比较两个班的平均成绩,应选择哪个数据的代表( )
A、平均数 B、中位数 C、众数
(3)、在学校组织的卡拉OK比赛中,你想知道自己在所有选手中处于什么水平,应该选择哪个数据的代表( )
A、平均数 B、中位数 C、众数
C
A
B
试一试
2、选择
3、 我们4班的教室里,三位同学正在为谁的数学成绩最好而争论,他们的5次数学成绩分别为:
昊华:62, 94, 95, 98, 98;
康伟:62,62,98, 99, 100;
郭良:40, 62,85, 99,99.
他们都认为自己的成绩比另两位同学的好,你能讲出他们认为好的理由吗
活学活用
……
1、知道了什么是中位数和众数。
2、会求一组数据的中位数和众数,
3、求中位数时一定要先排序,而且总数奇、偶时有所不同。
4、 平均数、中位数和众数从不同的侧面描述了一组数据的集中趋势。
……
本节课我收获了
1. 课本习题20.2 第1,2题。
2. 收集本班同学体重数据 ,并求出本班学生体重的的平均数、中位数、
众数.
一个成功的竞争者应该经得起风雨,
应该具有抗挫折的能力。
教师寄语
4、从甲、乙、丙三个厂家生产的产品冰箱分别随机抽取10台,对其使用寿命跟踪调查,结果如下:
(单位:年)
甲:6,7,8,12,10,10,12,9,10,10,
乙:8,9,8,9,10,12,11,11,10,12;
丙:7,7,8,8,9,11,11,12,12,13;
三个厂家在广告中都称该产品的使用寿命是10年。
你能用所学的知识来解释使用寿命为什么都是10年吗
厂家在广告中分别运用了平均数、众数、中位数
的哪一种特征数:甲 ,乙 ,
丙 .
众数
平均数
中位数
试一试
问题情景:据中国气象局2011年10月20日19时30预报,
2011年10月20日预报21的各地最高气温(℃)
北京 17 天津 22 石家庄 21 太原 21 呼和浩特 18 沈阳 22 长春 20 哈尔滨
19
上海 23 南京 23 杭州 24 合肥 22 福州 27 南昌 26 济南 23 郑州
22
武汉 25 长沙 26 广州 30 海口 30 南宁 29 成都 21 重庆 20 贵阳
17
昆明 20 拉萨 20 西安 21 兰州 18 银川 20 西宁 16 乌鲁木齐 9
求一组数据的中位数的方法:
1.排序(从小到大或从大到小)
2.正中间一个数(或正中间两个数的平
均数)
注意:
1、奇数个数据、偶数个数据求中位数时有区别
2、每一组数据都有中位数
平均数 中位数 众数
不 同 点 是否存在 存在 存在 可有可无
个数 1 1 没有、1个或多个
受极值影响 受 不受 不受
数据特征 平均水平 中等水平 多数水平
确定方法 公式 排序 计数
共同点 都是描述一组数据的集中趋势 平均数是概括一组数据的一种常用指标,反映了这组数据中各数据的平均大小.
中位数是概括一组数据的另一种指标,如果将一组数据按由小到大的顺序排列(即使有相等的数据也要全部参加排列),那么中位数的左边和右边恰有一样多的数据.
众数告诉我们,这个值出现的次数最多.一组数据可以有不止一个众数,也可能没有众数.
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工
月薪(元) 12000 8000 3200 2800 2500 2500 2500 2500 1000
你能用本节课所学的知识来分析这组数据吗
谢 谢
