华东师大版七年级下册数学 9.1.1 认识三角形 课件(共28张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 9.1.1 认识三角形 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
认识三角形
熊大熊二的难题
怎样切可以保证他们俩吃的面积一样大呢???
CONTENTS
目录
带着目标去旅行
01
探索新知
02
课堂小结
03
知识运用—小组展示
04
随堂测试
05
拓展提升
06
PART 01
带着目标去“旅行”
有目标才有动力!!!
带着目标去“旅行”
掌握三角形的角平分线、中线、高线的概念,并会画出任意三角形的角平分线、中线、高线
掌握三角形的三条中线、角平分线、高所在直线分别交于一点及交点的位置
会利用三角形的高、角平分线、中线解决实际问题
有目标才有动力!!!
PART 02
探索新知
重要的宝贝在这里哦!!!
三角形的高
概念:从三角形的一个顶点向它的对边所在的直线做一条垂线,顶点和垂足之间的线段叫做三角形的高,三角形有3条高。
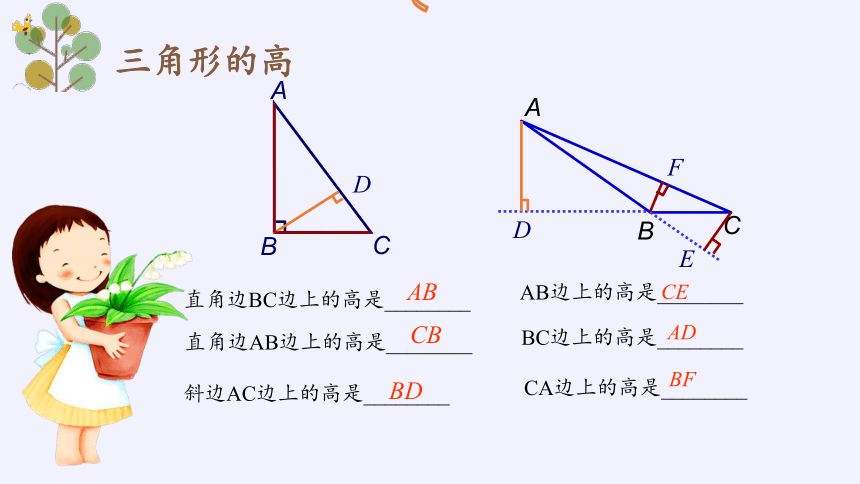
三角形的高
直角边BC边上的高是________
AB
CB
A
B
C
D
E
F
A
B
C
D
BD
CE
AD
BF
直角边AB边上的高是________
斜边AC边上的高是________
AB边上的高是________
BC边上的高是________
CA边上的高是________
三角形的高
如何画一个三角形的三条高呢?
一靠边
二过顶点
三画线
三角形的高
锐角三角形 直角三角形 钝角三角形
高在图中的位置 全在三角形内部 一条高在三角形________ 另两条高与_______重合 一条在三角形______
两条在三角形______
交点位置 三角形 _______ ______________ 三条高无交点
三条高所在的直线交于三角形_________
内部
直角边
内部
外部
内部
交于直角顶点处
外部
三角形的高
高的表示与作用:
表示:(1)AD是△ABC的高
(2)AD是△ABC中BC边上的高
(3)AD⊥BC于点D
(4)∠ADC=90°(或∠ADB=90°)
作用 : ∵AD是△ABC的高
∴(1)AD⊥BC(线段垂直)
(2)∠ADB=∠ADC=90°(90度的角)
A
D
C
B
三角形的角平分线
1.概念:三角形中,一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线,三角形有______条角平分线。
2.角的角平分线是一条_____,三角形的角平分线是一条_____。
3.探究结果:三角形的三条角平分线都能相交于一点,且交点都在三角形的_____。
三角形的角平分线
角平分线的表示与作用:
表示:
(1)AD是△ABC的角平分线
(2)AD平分∠BAC,交BC于D
(3)∠1=∠2= ∠BAC
作用 :
∵AD是△ABC的角平分线
∴∠1=∠2= ∠BAC ∠BAC=2∠1=2∠2
A
D
C
B
1
2
三角形的中线
1.概念:三角形中,连接一个顶点和它所对的边的中点之间的线段叫三角形的中线,三角形有______条中线。
2.探究结果:三角形的三条中线都能相交于一点,且交点都在三角形的_____,我们称这个交点为三角形的重心。
三角形的中线
中线平分面积:沿着中线将一个三角形剪开,分成的两个三角形的面积是相等的。
A
D
E
C
B
已知AD是△ABC的高,AE是△ABC的中线
分成的两个小三角形等底等高
三角形的中线
A
D
C
B
中线的表示与作用:
表示:(1)AD是△ABC的中线
(2)AD是△ABC中BC边上的中线
(3)BD=DC= BC
作用 :∵AD是△ABC的中线
∴(1)BD=CD= BC BC=2BD=2DC(线段相等)
(2)S△ABD= S△ADC(平分面积)
熊大熊二的难题
沿着中线切开,熊大、熊二就可以吃的一样多了!
PART 03
课堂小结
课堂小结
1.高
(1)概念与画法(2)交点位置(3)特性
2.角平分线
(1)概念与画法(2)交点位置(3)特性
3.中线
(1)概念与画法(2)交点位置(3)特性
PART 04
知识运用
--小组展示
知识应用—小组展示
1.如图所示,AE是 △ ABC的角平分线.已知∠B=500, ∠C=600,则∠CAE=________,
∠AEB=____________。
A
E
C
B
知识应用—小组展示
C
D
A
B
2.如图所示,CD是△ABC的中线, △BCD的周长比△ACD的周长大3cm,BC=8cm,求AC.
解: ∵CD为△ABC的中线,
∴________=________
又∵ △BCD的周长比△ACD的周长大3cm
∴ (BC+BD+MC)-(AC+DC+AD)=3
即______-______=3cm
又∵BC=8cm
∴AC=_____cm
知识应用—小组展示
3.如图所示, 在△ABC中,AD是△ABC的高,AE是△ABC的角平分线。已知∠BAC=88°,∠B=55°,则∠DAE=_________。
E
D
C
B
A
PART 05
随堂测试
随堂测试
E
F
C
B
A
1.如左图所示,D、E、F都在BC上, AE是△ABC的角平分线, AF是△ABC的高。已知∠B=40°,∠C=30°,则∠CAE=________;∠BAE=_______;∠BAF=_______;∠FAE=______。
2.如右图所示,AD是△ABC的中线,AE是△ACD的中线,已知DE=2cm,则BD=_______,BE=_______,BC=________.
E
C
B
A
D
PART 06
拓展提升
拓展提升
1.如图所示,在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长.(结合第5题试着自己写过程)
2.已知△ABC中,AC=5cm。中线AD把△ABC分成两个小三角形,这两个小三角形的周长的差是2cm。则AB=_______________。
C
D
A
B
谢 谢
认识三角形
熊大熊二的难题
怎样切可以保证他们俩吃的面积一样大呢???
CONTENTS
目录
带着目标去旅行
01
探索新知
02
课堂小结
03
知识运用—小组展示
04
随堂测试
05
拓展提升
06
PART 01
带着目标去“旅行”
有目标才有动力!!!
带着目标去“旅行”
掌握三角形的角平分线、中线、高线的概念,并会画出任意三角形的角平分线、中线、高线
掌握三角形的三条中线、角平分线、高所在直线分别交于一点及交点的位置
会利用三角形的高、角平分线、中线解决实际问题
有目标才有动力!!!
PART 02
探索新知
重要的宝贝在这里哦!!!
三角形的高
概念:从三角形的一个顶点向它的对边所在的直线做一条垂线,顶点和垂足之间的线段叫做三角形的高,三角形有3条高。
三角形的高
直角边BC边上的高是________
AB
CB
A
B
C
D
E
F
A
B
C
D
BD
CE
AD
BF
直角边AB边上的高是________
斜边AC边上的高是________
AB边上的高是________
BC边上的高是________
CA边上的高是________
三角形的高
如何画一个三角形的三条高呢?
一靠边
二过顶点
三画线
三角形的高
锐角三角形 直角三角形 钝角三角形
高在图中的位置 全在三角形内部 一条高在三角形________ 另两条高与_______重合 一条在三角形______
两条在三角形______
交点位置 三角形 _______ ______________ 三条高无交点
三条高所在的直线交于三角形_________
内部
直角边
内部
外部
内部
交于直角顶点处
外部
三角形的高
高的表示与作用:
表示:(1)AD是△ABC的高
(2)AD是△ABC中BC边上的高
(3)AD⊥BC于点D
(4)∠ADC=90°(或∠ADB=90°)
作用 : ∵AD是△ABC的高
∴(1)AD⊥BC(线段垂直)
(2)∠ADB=∠ADC=90°(90度的角)
A
D
C
B
三角形的角平分线
1.概念:三角形中,一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线,三角形有______条角平分线。
2.角的角平分线是一条_____,三角形的角平分线是一条_____。
3.探究结果:三角形的三条角平分线都能相交于一点,且交点都在三角形的_____。
三角形的角平分线
角平分线的表示与作用:
表示:
(1)AD是△ABC的角平分线
(2)AD平分∠BAC,交BC于D
(3)∠1=∠2= ∠BAC
作用 :
∵AD是△ABC的角平分线
∴∠1=∠2= ∠BAC ∠BAC=2∠1=2∠2
A
D
C
B
1
2
三角形的中线
1.概念:三角形中,连接一个顶点和它所对的边的中点之间的线段叫三角形的中线,三角形有______条中线。
2.探究结果:三角形的三条中线都能相交于一点,且交点都在三角形的_____,我们称这个交点为三角形的重心。
三角形的中线
中线平分面积:沿着中线将一个三角形剪开,分成的两个三角形的面积是相等的。
A
D
E
C
B
已知AD是△ABC的高,AE是△ABC的中线
分成的两个小三角形等底等高
三角形的中线
A
D
C
B
中线的表示与作用:
表示:(1)AD是△ABC的中线
(2)AD是△ABC中BC边上的中线
(3)BD=DC= BC
作用 :∵AD是△ABC的中线
∴(1)BD=CD= BC BC=2BD=2DC(线段相等)
(2)S△ABD= S△ADC(平分面积)
熊大熊二的难题
沿着中线切开,熊大、熊二就可以吃的一样多了!
PART 03
课堂小结
课堂小结
1.高
(1)概念与画法(2)交点位置(3)特性
2.角平分线
(1)概念与画法(2)交点位置(3)特性
3.中线
(1)概念与画法(2)交点位置(3)特性
PART 04
知识运用
--小组展示
知识应用—小组展示
1.如图所示,AE是 △ ABC的角平分线.已知∠B=500, ∠C=600,则∠CAE=________,
∠AEB=____________。
A
E
C
B
知识应用—小组展示
C
D
A
B
2.如图所示,CD是△ABC的中线, △BCD的周长比△ACD的周长大3cm,BC=8cm,求AC.
解: ∵CD为△ABC的中线,
∴________=________
又∵ △BCD的周长比△ACD的周长大3cm
∴ (BC+BD+MC)-(AC+DC+AD)=3
即______-______=3cm
又∵BC=8cm
∴AC=_____cm
知识应用—小组展示
3.如图所示, 在△ABC中,AD是△ABC的高,AE是△ABC的角平分线。已知∠BAC=88°,∠B=55°,则∠DAE=_________。
E
D
C
B
A
PART 05
随堂测试
随堂测试
E
F
C
B
A
1.如左图所示,D、E、F都在BC上, AE是△ABC的角平分线, AF是△ABC的高。已知∠B=40°,∠C=30°,则∠CAE=________;∠BAE=_______;∠BAF=_______;∠FAE=______。
2.如右图所示,AD是△ABC的中线,AE是△ACD的中线,已知DE=2cm,则BD=_______,BE=_______,BC=________.
E
C
B
A
D
PART 06
拓展提升
拓展提升
1.如图所示,在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长.(结合第5题试着自己写过程)
2.已知△ABC中,AC=5cm。中线AD把△ABC分成两个小三角形,这两个小三角形的周长的差是2cm。则AB=_______________。
C
D
A
B
谢 谢
