华东师大版八年级下册数学 阅读材料 完美矩形 教案
文档属性
| 名称 | 华东师大版八年级下册数学 阅读材料 完美矩形 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 149.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 10:06:42 | ||
图片预览

文档简介
课题:《矩形中的折叠问题》
教学目标:
知识与技能:
1.掌握轴对称变换中的角度、线段长度、面积和周长的计算方法
2.积累综合运用数学知识、技能和方法等解决简单的数学活动经验
数学思考:
1.建立折叠的空间观念,形成几何直观,发展学生的形象思维与抽象思维
2.学会独立思考,体会数学的基本思想和思维方式
问题解决:
1.学会从数学的角度发现问题和提出问题
2.综合运用数学知识解决简单的实际问题,增强应用意识,增强实践能力
情感态度:
在学习过程中,体验获得成功的乐趣,锻炼克服困难的意志,建立自信心
重点:利用折叠中的轴对称变换是解决问题
难点:综合运用所学知识解决折叠中的问题
教具准备:PPT课件 学具准备:矩形纸
教学过程:
问题与情境 师生行为 设计意图
(一)情境导入矩形的性质独特,折叠起来形态各异,趣味无穷,二者的结合产生了丰富多彩的几何问题。请大家欣赏一组矩形折纸图片总结折叠的性质:(本质是轴对称)1.图形的全等性:折叠前后的图形是全等形 2.点的对称性:对称点的连线被对称轴(折痕)垂直平分 教师引导,让学生回忆熟悉的生活经验,并播放一组矩形折纸作品图片,激发学生的学习兴趣,导入课题 激发兴趣、导入课题
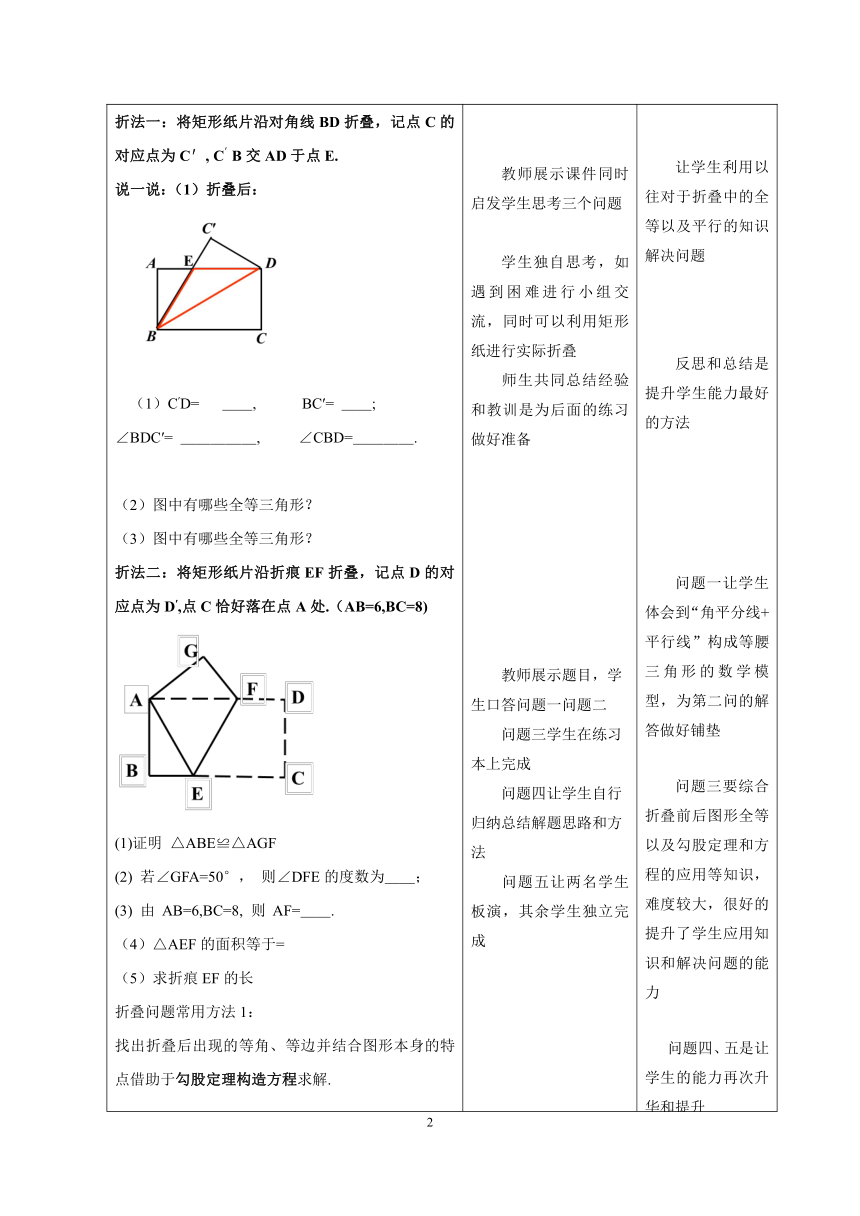
折法一:将矩形纸片沿对角线BD折叠,记点C的对应点为C′, C′B交AD于点E.说一说:(1)折叠后: (1)C′D= __, BC′= __;∠BDC′= _____, ∠CBD=____.(2)图中有哪些全等三角形? (3)图中有哪些全等三角形? 折法二:将矩形纸片沿折痕EF折叠,记点D的对 应点为D′,点C恰好落在点A处.(AB=6,BC=8)(1)证明 △ABE≌△AGF(2) 若∠GFA=50°, 则∠DFE的度数为__;(3) 由 AB=6,BC=8, 则 AF=__.(4)△AEF的面积等于= (5)求折痕EF的长折叠问题常用方法1:找出折叠后出现的等角、等边并结合图形本身的特点借助于勾股定理构造方程求解. 教师展示课件同时启发学生思考三个问题学生独自思考,如遇到困难进行小组交流,同时可以利用矩形纸进行实际折叠师生共同总结经验和教训是为后面的练习做好准备教师展示题目,学生口答问题一问题二问题三学生在练习本上完成问题四让学生自行归纳总结解题思路和方法问题五让两名学生板演,其余学生独立完成 让学生利用以往对于折叠中的全等以及平行的知识解决问题反思和总结是提升学生能力最好的方法问题一让学生体会到“角平分线+平行线”构成等腰三角形的数学模型,为第二问的解答做好铺垫问题三要综合折叠前后图形全等以及勾股定理和方程的应用等知识,难度较大,很好的提升了学生应用知识和解决问题的能力问题四、五是让学生的能力再次升华和提升问题四利用练习巩固上面的结论
折法三:将矩形ABCD沿折痕AE折叠,使点D落在BC边上的点F处.(1)△ABF与△FCE相似吗? (2)求EC的长. 在矩形折叠中,求线段的长度时,往往利用轴对称转化为相等的线段,然后构造方程。折叠问题常用方法2:利用相似三角形由相似比列方程求解.构造方程的方法:(1)用相似得到方程(2)把条件集中到一Rt△中, 根据勾股定理得方程直击中考已知:在矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数 的图象与AC边交于点E.(1)点E 的坐标为( ),点F ( ).(结果可以用k的代数式来表示)(2)用k的代数式表示出线段EC与CF的长4.对应练习(1).将一张长方形纸片按如图所示的方式折叠,BC、BD为折痕,则∠CBD的度数为( )A.60° B.75° C.90° D.95°(2).如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于( )A.50° B.55° C.60 ° D.65° 教师多媒体展示,学生独立完成学生口答的形式回答练习 巩固得出的结论
(3)请探索:是否存在这样的点F,使得将△CEF沿EF对折后,C点恰好落在OB上?若存在,求出点F的坐标;若不存在,请说明理由. 教师展示题目,学生口答问题一问题二学生在练习本上完成问题三让学生自行归纳总结 问题一让学生体会到“角平分线+平行线”构成等腰三角形的数学模型,为第二问的解答做好铺垫问题二要综合折叠前后图形全等以及勾股定理和方程的应用等知识,难度较大,很好的提升了学生应用知识和解决问题的能力问题三是让学生的能力再次升华和提升
教师展示题目后,学生先独立的尝试解决,如有困难可以小组交流或动手折纸尝试找方法教师引导学生尝试不同的思路完成学生展示不同的思路 探究三是探究一、二的综合应用,因此是学生的能力是一个质的提升,这对学生解决问题的能力得到了很好的锻炼
感悟与收获(1)折叠过程实质上是一个轴对称变换,折痕就是对称轴,变换前后两个图形全等。(2)在矩形的折叠问题中,若有求边长问题,常设未知数,找到相应的直角三角形,用勾股定理建立方程,或通过相似,用线段成比例建立方程,利用方程思想解决问题。(3)在折叠问题中,若直接解决较困难时,可将图形还原,可让问题变得简单明了。有时还可采用动手操作,通过折叠观察得出问题的答案。 教师引导学生从方法、体验、知识三个方面说明自己的收获和经验. 通过回顾和反思,成为提高教师自身与学生素质的互动过程
5
教学目标:
知识与技能:
1.掌握轴对称变换中的角度、线段长度、面积和周长的计算方法
2.积累综合运用数学知识、技能和方法等解决简单的数学活动经验
数学思考:
1.建立折叠的空间观念,形成几何直观,发展学生的形象思维与抽象思维
2.学会独立思考,体会数学的基本思想和思维方式
问题解决:
1.学会从数学的角度发现问题和提出问题
2.综合运用数学知识解决简单的实际问题,增强应用意识,增强实践能力
情感态度:
在学习过程中,体验获得成功的乐趣,锻炼克服困难的意志,建立自信心
重点:利用折叠中的轴对称变换是解决问题
难点:综合运用所学知识解决折叠中的问题
教具准备:PPT课件 学具准备:矩形纸
教学过程:
问题与情境 师生行为 设计意图
(一)情境导入矩形的性质独特,折叠起来形态各异,趣味无穷,二者的结合产生了丰富多彩的几何问题。请大家欣赏一组矩形折纸图片总结折叠的性质:(本质是轴对称)1.图形的全等性:折叠前后的图形是全等形 2.点的对称性:对称点的连线被对称轴(折痕)垂直平分 教师引导,让学生回忆熟悉的生活经验,并播放一组矩形折纸作品图片,激发学生的学习兴趣,导入课题 激发兴趣、导入课题
折法一:将矩形纸片沿对角线BD折叠,记点C的对应点为C′, C′B交AD于点E.说一说:(1)折叠后: (1)C′D= __, BC′= __;∠BDC′= _____, ∠CBD=____.(2)图中有哪些全等三角形? (3)图中有哪些全等三角形? 折法二:将矩形纸片沿折痕EF折叠,记点D的对 应点为D′,点C恰好落在点A处.(AB=6,BC=8)(1)证明 △ABE≌△AGF(2) 若∠GFA=50°, 则∠DFE的度数为__;(3) 由 AB=6,BC=8, 则 AF=__.(4)△AEF的面积等于= (5)求折痕EF的长折叠问题常用方法1:找出折叠后出现的等角、等边并结合图形本身的特点借助于勾股定理构造方程求解. 教师展示课件同时启发学生思考三个问题学生独自思考,如遇到困难进行小组交流,同时可以利用矩形纸进行实际折叠师生共同总结经验和教训是为后面的练习做好准备教师展示题目,学生口答问题一问题二问题三学生在练习本上完成问题四让学生自行归纳总结解题思路和方法问题五让两名学生板演,其余学生独立完成 让学生利用以往对于折叠中的全等以及平行的知识解决问题反思和总结是提升学生能力最好的方法问题一让学生体会到“角平分线+平行线”构成等腰三角形的数学模型,为第二问的解答做好铺垫问题三要综合折叠前后图形全等以及勾股定理和方程的应用等知识,难度较大,很好的提升了学生应用知识和解决问题的能力问题四、五是让学生的能力再次升华和提升问题四利用练习巩固上面的结论
折法三:将矩形ABCD沿折痕AE折叠,使点D落在BC边上的点F处.(1)△ABF与△FCE相似吗? (2)求EC的长. 在矩形折叠中,求线段的长度时,往往利用轴对称转化为相等的线段,然后构造方程。折叠问题常用方法2:利用相似三角形由相似比列方程求解.构造方程的方法:(1)用相似得到方程(2)把条件集中到一Rt△中, 根据勾股定理得方程直击中考已知:在矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数 的图象与AC边交于点E.(1)点E 的坐标为( ),点F ( ).(结果可以用k的代数式来表示)(2)用k的代数式表示出线段EC与CF的长4.对应练习(1).将一张长方形纸片按如图所示的方式折叠,BC、BD为折痕,则∠CBD的度数为( )A.60° B.75° C.90° D.95°(2).如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于( )A.50° B.55° C.60 ° D.65° 教师多媒体展示,学生独立完成学生口答的形式回答练习 巩固得出的结论
(3)请探索:是否存在这样的点F,使得将△CEF沿EF对折后,C点恰好落在OB上?若存在,求出点F的坐标;若不存在,请说明理由. 教师展示题目,学生口答问题一问题二学生在练习本上完成问题三让学生自行归纳总结 问题一让学生体会到“角平分线+平行线”构成等腰三角形的数学模型,为第二问的解答做好铺垫问题二要综合折叠前后图形全等以及勾股定理和方程的应用等知识,难度较大,很好的提升了学生应用知识和解决问题的能力问题三是让学生的能力再次升华和提升
教师展示题目后,学生先独立的尝试解决,如有困难可以小组交流或动手折纸尝试找方法教师引导学生尝试不同的思路完成学生展示不同的思路 探究三是探究一、二的综合应用,因此是学生的能力是一个质的提升,这对学生解决问题的能力得到了很好的锻炼
感悟与收获(1)折叠过程实质上是一个轴对称变换,折痕就是对称轴,变换前后两个图形全等。(2)在矩形的折叠问题中,若有求边长问题,常设未知数,找到相应的直角三角形,用勾股定理建立方程,或通过相似,用线段成比例建立方程,利用方程思想解决问题。(3)在折叠问题中,若直接解决较困难时,可将图形还原,可让问题变得简单明了。有时还可采用动手操作,通过折叠观察得出问题的答案。 教师引导学生从方法、体验、知识三个方面说明自己的收获和经验. 通过回顾和反思,成为提高教师自身与学生素质的互动过程
5
