北师大版七年级下册1.2 幂的乘方与积的乘方 课件(共19张PPT)
文档属性
| 名称 | 北师大版七年级下册1.2 幂的乘方与积的乘方 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 343.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 10:18:52 | ||
图片预览





文档简介
(共19张PPT)
课题:幂的乘方与积的乘方(2)
学习目标
1.理解并掌握积的乘方的运算法则;(重点)
2.掌握积的乘方的推导过程,并能灵活运用.(难点)
复习回顾
1.幂的意义:an表示 ;
2.同底数幂的乘法:
语言叙述:同底数幂相乘,底数 ,指数 .
字母表示:am·an= ( m,n都是正整数)
am+n
3.幂的乘方:
语言叙述:幂的乘方,底数 ,指数 .
字母表示:(am)n= (m,n都是正整数).
amn
不变
相加
不变
相乘
n个a相乘
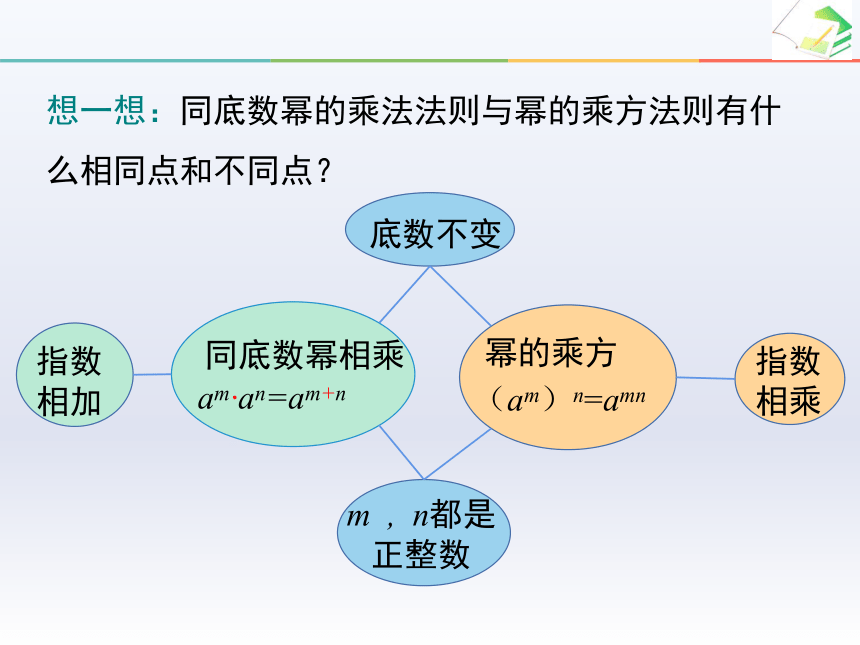
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
同底数幂相乘
am·an=am+n
幂的乘方
(am)n=amn
指数
相加
指数
相乘
底数不变
m , n都是正整数
探究活动
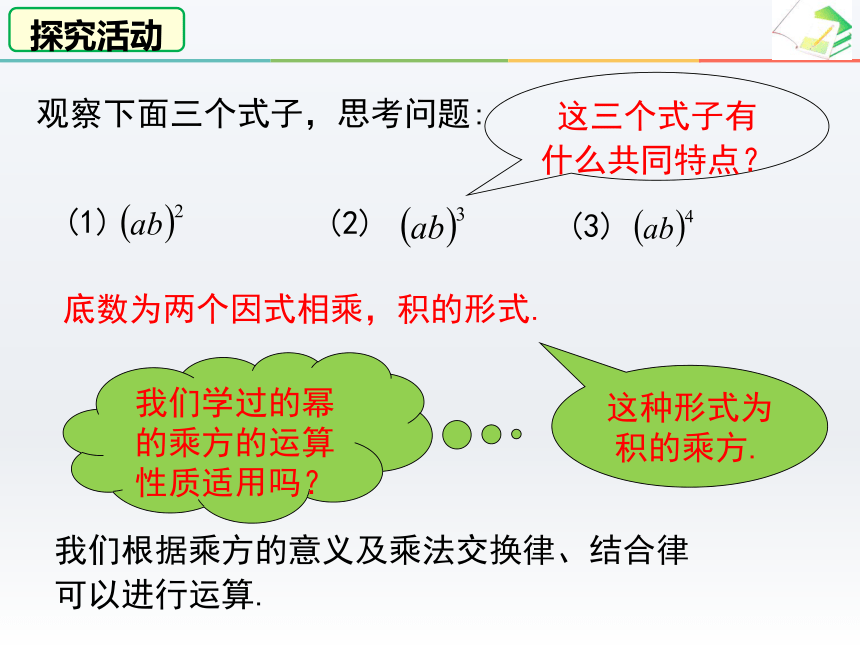
观察下面三个式子,思考问题:
(1)
(2)
(3)
这三个式子有什么共同特点?
底数为两个因式相乘,积的形式.
这种形式为积的乘方.
我们学过的幂的乘方的运算性质适用吗?
我们根据乘方的意义及乘法交换律、结合律
可以进行运算.
同理:
(乘方的意义)
(乘法交换律、结合律)
(乘方的意义)
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
=anbn.
证明:
推理思考:积的乘方 (ab)n =
猜想结论:
因此可得:(ab)n=anbn (n为正整数).
(ab)n=anbn (n为正整数)
(乘方的意义)
(乘法交换律、结合律)
(乘方的意义)
积的乘方法则:积的乘方等于每一个因式乘方的积.
(ab)n = anbn (n为正整数)
思维拓展:三个或三个以上因式的积的乘方等于什么?
积的乘方
乘方的积
例1 计算:
(1)(3x)2 ; (2)(-2b)5 ;
(3)(-2xy)4 ; (4)(3a2)n.
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
= 9x2;
= -32b5;
=16x4y4;
=3na2n.
32x2
(-2)5b5
(-2)4x4y4
3n(a2)n
方法总结:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数也要乘方.
典例精析
例2 计算:
典例精析
(1)
(2)
(3)
(4)
解:(1)原式=
(-2)2x2y2(z2)2
=4x2y2z4
(2)原式=
(-3)3[(n-m)2]3
=-27(n-m)6
(3)原式=
(cn)2(dn-1)2(c2)ndn
=c2nd2n-2c2ndn
=c4nd3n-2
(4)原式=
(-3)2(x3)2-(2x)6
=9x6-26x6
=9x6-64x6
=-55x6
思维拓展
思考:积的乘方运算法则能否进行逆运算呢?
(n是正整数)
乘方的积
积的乘方
(乘方的意义)
(乘法交换律、结合律)
(乘方的意义)
?
例3
小明的作业
计算:
上面是小明完成的一道计算,请你参考小明的方法进行计算:
典例精析
逆用同底数幂的乘法运算性质
逆用积的乘方的运算性质
解:原式
逆用同底数幂的乘法运算
性质
逆用积的乘方的运算性质
典例精析
知识小结
an·bn = (ab)n
am+n =am·an
amn =(am)n
作用:
使运算更加简便快捷!
幂的运算法则的逆向应用
(1)(ab2)3=ab6 ; ( )
×
×
×
(2) (3xy)3=9x3y3 ; ( )
×
(3) (-2a2)2=-4a4 ; ( )
(4) -(-ab2)2=a2b4 . ( )
1.判断:
2.下列运算正确的是( )
A.x.x2=x2 B.(xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
C
3. (0.04)2020×(-25)2020=________.
1
自主练习
(1) (ab)8; (2) (2m)3; (3) (-xy)5;
(4) (5ab2)3; (5) (2×102)2; (6) (-3×103)3.
4.计算:
解:(1)原式=a8·b8;
(2)原式= 23 ·m3=8m3;
(3)原式=(-x)5 ·y5=-x5y5;
(4)原式=53 ·a3 ·(b2)3=125a3b6;
(5)原式=22 ×(102)2=4 ×104;
(6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010.
(1)2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
(3)(-2x3)3·(x2)2.
解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9 = 0;
解:原式=9x2y4 +4x2y4
=13x2y4;
解:原式= -8x9·x4 =-8x13.
注意:运算顺序是先乘方,再乘除,最后算加减.
5.计算:
能力提升:如果(an.bm.b)3=a9b15,求m, n的值.
(an)3.(bm)3.b3=a9b15,
a3n .b3m.b3=a9b15 ,
a3n.b3m+3=a9b15,
3n=9,3m+3=15.
n=3,m=4.
解:∵(an.bm.b)3=a9b15,
通过本节课的学习,你有什么收获、疑惑?
幂的运算性质
性质
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都是正整数)
逆向运用
am+n=am · an
amn= (am)n
an·bn = (ab)n (m、n都是正整数)
可使某些计算简捷
注意
运用积的乘方法则时要注意:
公式中的a、b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)
课堂小结
课题:幂的乘方与积的乘方(2)
学习目标
1.理解并掌握积的乘方的运算法则;(重点)
2.掌握积的乘方的推导过程,并能灵活运用.(难点)
复习回顾
1.幂的意义:an表示 ;
2.同底数幂的乘法:
语言叙述:同底数幂相乘,底数 ,指数 .
字母表示:am·an= ( m,n都是正整数)
am+n
3.幂的乘方:
语言叙述:幂的乘方,底数 ,指数 .
字母表示:(am)n= (m,n都是正整数).
amn
不变
相加
不变
相乘
n个a相乘
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
同底数幂相乘
am·an=am+n
幂的乘方
(am)n=amn
指数
相加
指数
相乘
底数不变
m , n都是正整数
探究活动
观察下面三个式子,思考问题:
(1)
(2)
(3)
这三个式子有什么共同特点?
底数为两个因式相乘,积的形式.
这种形式为积的乘方.
我们学过的幂的乘方的运算性质适用吗?
我们根据乘方的意义及乘法交换律、结合律
可以进行运算.
同理:
(乘方的意义)
(乘法交换律、结合律)
(乘方的意义)
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
=anbn.
证明:
推理思考:积的乘方 (ab)n =
猜想结论:
因此可得:(ab)n=anbn (n为正整数).
(ab)n=anbn (n为正整数)
(乘方的意义)
(乘法交换律、结合律)
(乘方的意义)
积的乘方法则:积的乘方等于每一个因式乘方的积.
(ab)n = anbn (n为正整数)
思维拓展:三个或三个以上因式的积的乘方等于什么?
积的乘方
乘方的积
例1 计算:
(1)(3x)2 ; (2)(-2b)5 ;
(3)(-2xy)4 ; (4)(3a2)n.
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
= 9x2;
= -32b5;
=16x4y4;
=3na2n.
32x2
(-2)5b5
(-2)4x4y4
3n(a2)n
方法总结:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数也要乘方.
典例精析
例2 计算:
典例精析
(1)
(2)
(3)
(4)
解:(1)原式=
(-2)2x2y2(z2)2
=4x2y2z4
(2)原式=
(-3)3[(n-m)2]3
=-27(n-m)6
(3)原式=
(cn)2(dn-1)2(c2)ndn
=c2nd2n-2c2ndn
=c4nd3n-2
(4)原式=
(-3)2(x3)2-(2x)6
=9x6-26x6
=9x6-64x6
=-55x6
思维拓展
思考:积的乘方运算法则能否进行逆运算呢?
(n是正整数)
乘方的积
积的乘方
(乘方的意义)
(乘法交换律、结合律)
(乘方的意义)
?
例3
小明的作业
计算:
上面是小明完成的一道计算,请你参考小明的方法进行计算:
典例精析
逆用同底数幂的乘法运算性质
逆用积的乘方的运算性质
解:原式
逆用同底数幂的乘法运算
性质
逆用积的乘方的运算性质
典例精析
知识小结
an·bn = (ab)n
am+n =am·an
amn =(am)n
作用:
使运算更加简便快捷!
幂的运算法则的逆向应用
(1)(ab2)3=ab6 ; ( )
×
×
×
(2) (3xy)3=9x3y3 ; ( )
×
(3) (-2a2)2=-4a4 ; ( )
(4) -(-ab2)2=a2b4 . ( )
1.判断:
2.下列运算正确的是( )
A.x.x2=x2 B.(xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
C
3. (0.04)2020×(-25)2020=________.
1
自主练习
(1) (ab)8; (2) (2m)3; (3) (-xy)5;
(4) (5ab2)3; (5) (2×102)2; (6) (-3×103)3.
4.计算:
解:(1)原式=a8·b8;
(2)原式= 23 ·m3=8m3;
(3)原式=(-x)5 ·y5=-x5y5;
(4)原式=53 ·a3 ·(b2)3=125a3b6;
(5)原式=22 ×(102)2=4 ×104;
(6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010.
(1)2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
(3)(-2x3)3·(x2)2.
解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9 = 0;
解:原式=9x2y4 +4x2y4
=13x2y4;
解:原式= -8x9·x4 =-8x13.
注意:运算顺序是先乘方,再乘除,最后算加减.
5.计算:
能力提升:如果(an.bm.b)3=a9b15,求m, n的值.
(an)3.(bm)3.b3=a9b15,
a3n .b3m.b3=a9b15 ,
a3n.b3m+3=a9b15,
3n=9,3m+3=15.
n=3,m=4.
解:∵(an.bm.b)3=a9b15,
通过本节课的学习,你有什么收获、疑惑?
幂的运算性质
性质
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都是正整数)
逆向运用
am+n=am · an
amn= (am)n
an·bn = (ab)n (m、n都是正整数)
可使某些计算简捷
注意
运用积的乘方法则时要注意:
公式中的a、b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)
课堂小结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
