华东师大版八年级下册数学 17.3.2 一次函数的图象 教案
文档属性
| 名称 | 华东师大版八年级下册数学 17.3.2 一次函数的图象 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 86.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 10:27:46 | ||
图片预览

文档简介
一次函数的图象
一、教学目标
1、通过实际问题,使学生感受一次函数、正比例函数的特点。
2、画出正比例函数、一次函数的图象,并会研究函数图象的性质。
二、教学重点与难点
画出一次函数的图象,并会研究函数图象的特征及性质
三、教学过程
㈠、新课引入
1、情境导入
t(时) 1 2 3 4 5 t
S(千米) S=
汽车以60千米∕时的速度匀速行驶,行驶里程为S千米,行驶时间为t小时,填写下表,并试用含t的式子表示S:
2、回忆正比例函数、一次函数的概念
形如(是常数,)的函数叫做正比例函数。
形如(是常数,)的函数叫做一次函数。
㈡、探索正比例函数的图象
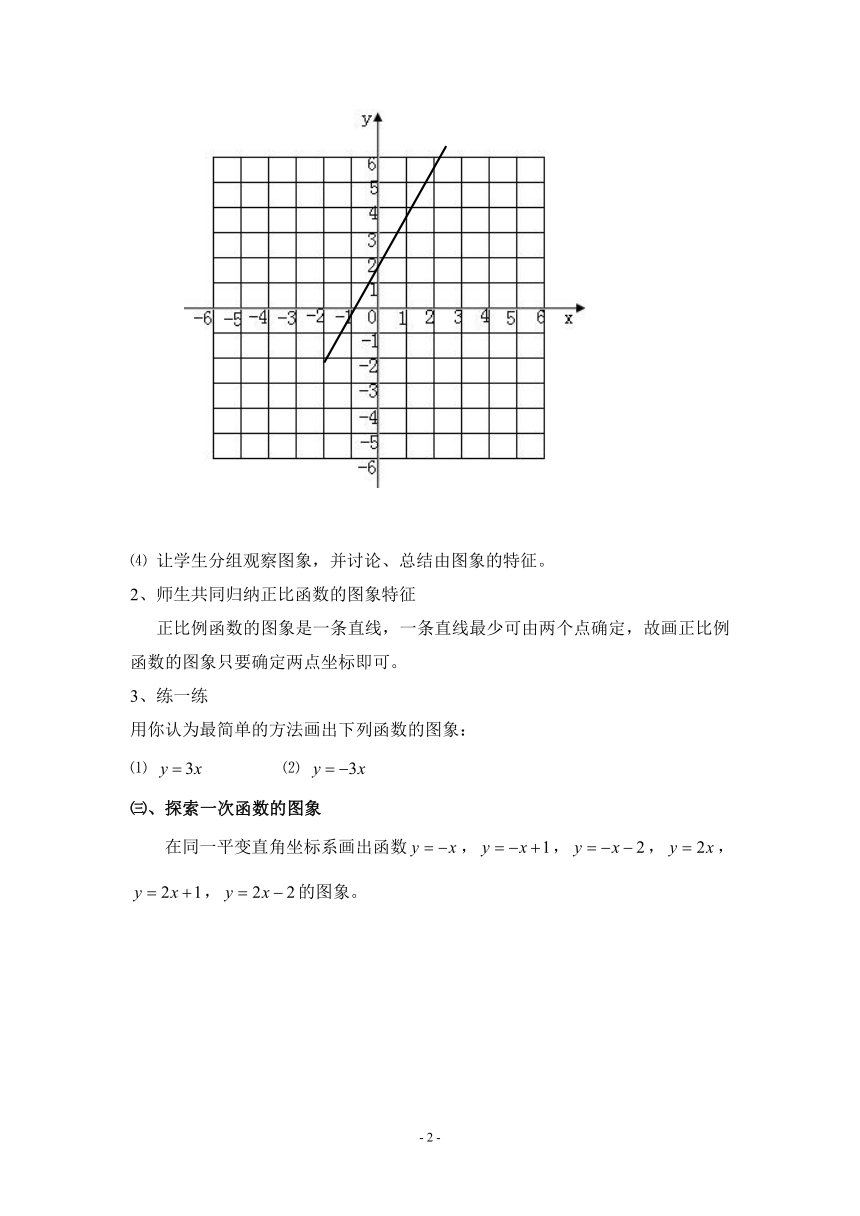
1、画出正比例函数的图象
解:⑴ 列表:
x -3 -2 -1 0 1 2 3
y
⑵ 描点 (在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的点);
⑶ 连线(用平滑曲线连接这些点)
⑷ 让学生分组观察图象,并讨论、总结由图象的特征。
2、师生共同归纳正比函数的图象特征
正比例函数的图象是一条直线,一条直线最少可由两个点确定,故画正比例函数的图象只要确定两点坐标即可。
3、练一练
用你认为最简单的方法画出下列函数的图象:
⑴ ⑵
㈢、探索一次函数的图象
在同一平变直角坐标系画出函数,,,,,的图象。
(
O
2
3
4
5
6
-1
-2
-3
-4
-5
-6
-2
-3
-4
-5
-6
1
2
3
4
5
-1
1
7
6
(
0
,
1
)
(
0
,
-2
)
)
⑴ 观察图象,归纳图象的平移特征。
函数的图象可看作由直线向上平移1个单位而得到,函数的图象可看作由直线向下平移2个单位而得到;
函数的图象可看作由直线向上平移1个单位而得到,函数的图象可看作由直线向下平移2个单位而得到。
⑵ 观察图象,探索并归纳一次函数图象位置与、取值的关系。
当相等,而不等时,两直线平行。比如图象中的直线,,互相平行,直线,,互相平行。
当、都相等时,两直线重合。
当不等时,两直线相交,此时,若相等,则两直线与轴交于一点,交点的坐标为(0,)。比如图象中的直线与直线的交点在轴上,交点坐标是(0,1)。
㈣、随堂练习
1、直线的图象是由正比例函数向 平移 个单位得到。
2、直线的图象是由正比例函数向 平移 个单位得到。
3、当时,函数的图象经过第 象限,随的增大而 。
4、当时,函数的图象经过第 象限,随的增大而 。
四、课堂小结
1、知道一次函数的图象是一条直线,画一次函数图象时,只要取两个点即可,一般取与坐标轴的交点。
2、两个一次函数,当一样,而不一样时,共同之处是这两条直线平行,都是由向上或向下移动得到,不同之处是它们与轴的交点不同;当一样,而不一样时,共同之处是它们与轴交于同一点(0,b),不同之处是这两条直线不平行。
五、板书设计
(
一次函数
的图象
回忆:一次函数及正比例函数的概念。
描点法
画一次函数的图象。
步骤:列表→描点→连线
图象特征:直线,两点可确定一条直线
探索一次函数的图象
两直线特殊位置关系的探索。
两直线位置变换(平移)的探索。
)
六、布置作业
课本习题18.3第4、5题。
- 1 -
一、教学目标
1、通过实际问题,使学生感受一次函数、正比例函数的特点。
2、画出正比例函数、一次函数的图象,并会研究函数图象的性质。
二、教学重点与难点
画出一次函数的图象,并会研究函数图象的特征及性质
三、教学过程
㈠、新课引入
1、情境导入
t(时) 1 2 3 4 5 t
S(千米) S=
汽车以60千米∕时的速度匀速行驶,行驶里程为S千米,行驶时间为t小时,填写下表,并试用含t的式子表示S:
2、回忆正比例函数、一次函数的概念
形如(是常数,)的函数叫做正比例函数。
形如(是常数,)的函数叫做一次函数。
㈡、探索正比例函数的图象
1、画出正比例函数的图象
解:⑴ 列表:
x -3 -2 -1 0 1 2 3
y
⑵ 描点 (在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的点);
⑶ 连线(用平滑曲线连接这些点)
⑷ 让学生分组观察图象,并讨论、总结由图象的特征。
2、师生共同归纳正比函数的图象特征
正比例函数的图象是一条直线,一条直线最少可由两个点确定,故画正比例函数的图象只要确定两点坐标即可。
3、练一练
用你认为最简单的方法画出下列函数的图象:
⑴ ⑵
㈢、探索一次函数的图象
在同一平变直角坐标系画出函数,,,,,的图象。
(
O
2
3
4
5
6
-1
-2
-3
-4
-5
-6
-2
-3
-4
-5
-6
1
2
3
4
5
-1
1
7
6
(
0
,
1
)
(
0
,
-2
)
)
⑴ 观察图象,归纳图象的平移特征。
函数的图象可看作由直线向上平移1个单位而得到,函数的图象可看作由直线向下平移2个单位而得到;
函数的图象可看作由直线向上平移1个单位而得到,函数的图象可看作由直线向下平移2个单位而得到。
⑵ 观察图象,探索并归纳一次函数图象位置与、取值的关系。
当相等,而不等时,两直线平行。比如图象中的直线,,互相平行,直线,,互相平行。
当、都相等时,两直线重合。
当不等时,两直线相交,此时,若相等,则两直线与轴交于一点,交点的坐标为(0,)。比如图象中的直线与直线的交点在轴上,交点坐标是(0,1)。
㈣、随堂练习
1、直线的图象是由正比例函数向 平移 个单位得到。
2、直线的图象是由正比例函数向 平移 个单位得到。
3、当时,函数的图象经过第 象限,随的增大而 。
4、当时,函数的图象经过第 象限,随的增大而 。
四、课堂小结
1、知道一次函数的图象是一条直线,画一次函数图象时,只要取两个点即可,一般取与坐标轴的交点。
2、两个一次函数,当一样,而不一样时,共同之处是这两条直线平行,都是由向上或向下移动得到,不同之处是它们与轴的交点不同;当一样,而不一样时,共同之处是它们与轴交于同一点(0,b),不同之处是这两条直线不平行。
五、板书设计
(
一次函数
的图象
回忆:一次函数及正比例函数的概念。
描点法
画一次函数的图象。
步骤:列表→描点→连线
图象特征:直线,两点可确定一条直线
探索一次函数的图象
两直线特殊位置关系的探索。
两直线位置变换(平移)的探索。
)
六、布置作业
课本习题18.3第4、5题。
- 1 -
