2021-2022六年级下数学第二学期第二单元单元测试卷苏教版(含答案)
文档属性
| 名称 | 2021-2022六年级下数学第二学期第二单元单元测试卷苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 171.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 10:52:11 | ||
图片预览




文档简介
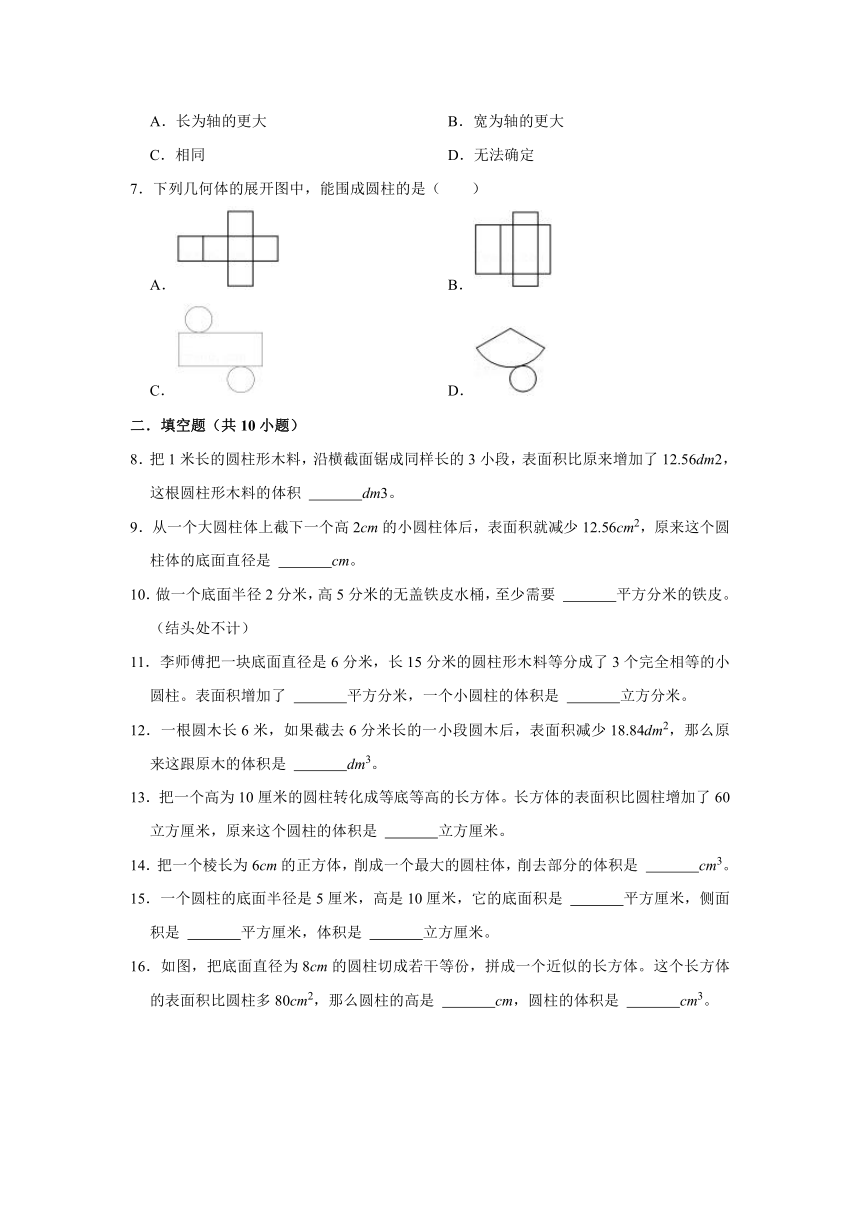
2021-2022六年级数学第二学期第二单元单元测试卷(八)
一.选择题(共7小题)
1.每个面都是正方形的立体图形是( )
A.长方体 B.正方体 C.圆柱
2.将一个圆柱沿底面直径横向切开后,得到的切面是个宽6cm,面积是60cm2的长方形(如图)。原来这个圆柱的体积是( )cm3。
A.188.4 B.282.6 C.360 D.1130.4
3.把一根底面半径是4分米,长是2米的圆柱形钢材截成两根小圆柱形钢材,这两根小圆柱形钢材的表面积之和与原来圆柱形钢材的表面积相比( )。
A.大小不变 B.增加了50.24平方分米
C.增加了100.48平方分米 D.增加了1004.8平方分米
4.将下面一个圆柱体沿着高剪开得到一个长方形,这个长方形的长是( )
A.4厘米 B.7厘米 C.21.98厘米
5.将下面的圆柱体的侧面沿AB展开,所得到的侧面展开图不可能是( )
A.①② B.①③ C.①②③ D.③④
6.如图,把一个长方形分别以长和宽为轴旋转一周形成的圆柱体,体积相比( )
A.长为轴的更大 B.宽为轴的更大
C.相同 D.无法确定
7.下列几何体的展开图中,能围成圆柱的是( )
A. B.
C. D.
二.填空题(共10小题)
8.把1米长的圆柱形木料,沿横截面锯成同样长的3小段,表面积比原来增加了12.56dm2,这根圆柱形木料的体积 dm3。
9.从一个大圆柱体上截下一个高2cm的小圆柱体后,表面积就减少12.56cm2,原来这个圆柱体的底面直径是 cm。
10.做一个底面半径2分米,高5分米的无盖铁皮水桶,至少需要 平方分米的铁皮。(结头处不计)
11.李师傅把一块底面直径是6分米,长15分米的圆柱形木料等分成了3个完全相等的小圆柱。表面积增加了 平方分米,一个小圆柱的体积是 立方分米。
12.一根圆木长6米,如果截去6分米长的一小段圆木后,表面积减少18.84dm2,那么原来这跟原木的体积是 dm3。
13.把一个高为10厘米的圆柱转化成等底等高的长方体。长方体的表面积比圆柱增加了60立方厘米,原来这个圆柱的体积是 立方厘米。
14.把一个棱长为6cm的正方体,削成一个最大的圆柱体,削去部分的体积是 cm3。
15.一个圆柱的底面半径是5厘米,高是10厘米,它的底面积是 平方厘米,侧面积是 平方厘米,体积是 立方厘米。
16.如图,把底面直径为8cm的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的表面积比圆柱多80cm2,那么圆柱的高是 cm,圆柱的体积是 cm3。
17.有一根长2米的圆柱形钢材,如果把它截成5个小圆柱,5个小圆柱的表面积之和比原来增加2512平方厘米。这根圆柱形钢材的体积是 立方厘米。
三.判断题(共7小题)
18.一个圆柱的底面半径是8厘米,它的侧面展开正好是一个正方形,这个圆柱的高是16厘米. .(判断对错)
19.圆柱的底面直径是3厘米,高3π厘米,侧面展开后是一个正方形. .(判断对错)
20.一个圆柱与一个圆锥底面积之比是2:3,高之比是4:5,体积之比是8:15。 (判断对错)
21.三角形绕着一条边旋转后形成的立体图形是圆锥。 (判断对错)
22.把一个圆柱切拼成一个和它体积相等的长方体,推导出圆柱体体积计算公式的这一过程中,运用了转化的数学思想方法。 (判断对错)
23.把一支新的圆柱形铅笔削尖,笔尖(圆锥部分)的体积是削去部分的。 (判断对错)
24.把一个圆柱体平均切成两个小圆柱,每个小圆柱体的体积和表面积都是原来圆柱体的一半。 (判断对错)
四.计算题(共2小题)
25.求如图的表面积和体积。(单位:cm)
26.计算下面圆柱的表面积.
五.应用题(共6小题)
27.一根圆柱形钢材,横截面的直径是10cm,长是150cm。如果加工一个零件需要用去钢材5cm3,这段钢材能生产多少个这种零件?
28.把一个底面半径是2厘米的圆柱体,沿底面直径垂直于高切成若干等份,再拼成一个近似长方体,(如图)已知拼成后长方体表面积比原来圆柱表面积增加了60平方厘米,这个长方体的体积是多少?
29.在一个棱长为3厘米的正方体上面正中央垂直向下挖出一个底面直径是2厘米,高为3厘米的圆柱,剩下物体的表面积为多少?
30.根据下如图玻璃容器中水的变化,你知道大正方体的体积是多少?
31.一个圆柱形粮囤,底面直径6米,装有2.5米高的小麦,这个粮囤有小麦多少立方米?
32.一个圆柱形玻璃容器里装有水,水中浸没着一个底面直径为12cm,高为10cm的圆锥形铁块,如果把它取出那么容器中的水面高度将下降多少厘米?(圆柱形玻璃容器的底面内直径是15厘米)
参考答案
一.选择题(共7小题)
1.解:每个面都是正方形的立体图形是正方体。
故选:B。
2.解:长方形的长:60÷6=10(cm)
圆柱的底面半径:6÷2=3(cm)
圆柱的体积:3.14×3 ×10
=3.14×9×10
=282.6(cm )
答:圆柱的体积是282.6cm 。
故选:B。
3.解:3.14×42×2
=3.14×16×2
=100.48(平方分米)
答:这两根小圆柱形钢材的表面积之和与原来圆柱形钢材的表面积相比增加了100.48平方分米。
故选:C。
4.解:3.14×7=21.98(cm)
答:展开后长方形的长是21.98厘米,C选项正确。
故选:C。
5.解:将圆的侧面沿高展开得到的图形只能为长方形或正方形,不可能是梯形或圆,所以D选项合适。
故选:D。
6.解:以长为轴旋转一周,得到的圆柱的体积:
3.14×42×8
=50.24×8
=401.92(立方厘米)
以宽为轴旋转一周,得到的圆柱的体积:
3.14×82×4
=200.96×4
=803.84(立方厘米)
401.92<803.84,所以以宽为轴旋转一周得到的圆柱体积大.
故选:B。
7.解:选项A,可以围成一个正方体,不符合题意。
选项B,可以围成一个长方体,不符合题意。
选项C,可以围成一个圆柱,符合题意。
选项D,可以围成一个圆锥,不符合题意。
故选:C。
二.填空题(共10小题)
8.解:1米=10分米
12.56÷4×10
=3.14×10
=31.4(dm )
答:这根圆柱形木料的体积31.4dm 。
故答案为:31.4。
9.解:12.56÷2÷3.14
=6.28÷3.14
=2(cm)
答:这个圆柱的底面直径是2cm。
故答案为:2。
10.解:3.14×2 +3.14×2×2×5
=3.14×4+62.8
=12.56+62.8
=75.36(平方分米)
答:至少需要75.36平方分米的铁皮。
故答案为:75.36。
11.解:3.14×(6÷2) ×4
=3.14×9×4
=113.04(平方分米)
3.14×(6÷2) ×15×
=3.14×9×15×
=423.9×
=141.3(立方分米)
答:表面积增加113.04平方分米,一个小圆柱的体积是141.3立方分米。
故答案为:113.04,141.3。
12.解:6米=60分米
18.84÷6=3.14(分米)
3.14÷3.14÷2=0.5(分米)
3.14×0.52×60
=3.14×0.25×60
=0.785×60
=47.1(立方分米)
答:原来这根圆木的体积是47.1立方分米。
故答案为:47.1。
13.解:60÷2÷10
=30÷10
=3(厘米)
3.14×32×10
=3.14×9×10
=28.26×10
=282.6(立方厘米)
答:原来这个圆柱的体积是282.6立方厘米。
故答案为:282.6。
14.解:6×6×6﹣3.14×(6÷2)2×6
=36×6﹣3.14×9×6
=216﹣169.56
=46.44(立方厘米)
答:削去部分的体积是46.44立方厘米。
故答案为:46.44。
15.解:3.14×52
=3.14×25
=78.5(平方厘米)
2×3.14×5×10
=31.4×10
=314(平方厘米)
3.14×52×10
=3.14×25×10
=78.5×10
=785(立方厘米)
答:它的底面积是78.5平方厘米,侧面积是314平方厘米,体积是785立方厘米。
故答案为:78.5、314、785。
16.解:80÷2÷(8÷2)
=40÷4
=10(厘米)
3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方厘米)
答:圆柱的高是10cm,圆柱的体积是502.4cm3。
故答案为:10cm,502.4cm3。
17.解:2米=200厘米
2512÷[(5﹣1)×2]×200
=2512÷[4×2]×200
=2512÷8×200
=314×200
=62800(立方厘米)
答:这根圆柱形钢材的体积是62800立方厘米。
故答案为:62800。
三.判断题(共7小题)
18.解:侧面展开后长方形的长(底面周长)=2πr=2×3.14×8=50.24(厘米);
又因为侧面展开后是正方形,所以:宽=长=50.24厘米;
侧面展开后长方形的宽又是圆柱的高,即高=50.24厘米;
故答案为:×.
19.解:侧面展开后长方形的长(底面周长)=3π厘米,
侧面展开后长方形的宽=圆柱的高=3π厘米,
因为:3π厘米=3π厘米,
所以:侧面展开后长方形的长=宽,此图形是正方形.
故答案为:√
20.解:设圆柱与圆锥的高分别是4h、5h,
圆柱的体积=2×3h=6h,
圆锥的体积=×3×5h=5h,
圆柱和圆锥体积的比是:6h:5h=6:5
答:圆柱和圆锥体积的比是6:5。
因此,题干中的结论是错误的。
故答案为:×。
21.解:如果是直角三角形,旋转一周,可以得到一个圆锥,否则不可能得到一个圆锥。
因此,三角形绕着一条边旋转后形成的立体图形是圆锥。此说法错误。
故答案为:×。
22.解:圆柱体积公式推导过程中,我们把圆柱转化为长方体,也就是把未知方法转化为已知方法,用到的是转化思想;
所以原题说法正确。
故答案为:√。
23.解:1﹣=
÷
=
=
笔尖(圆锥部分)的体积是削去部分的,原题说法正确。
故答案为:√。
24.解:根据分析可得,
把一个圆柱平均切成两个小圆柱,这两个小圆柱等底等高,根据圆柱的体积=底面积×高,可知这两个小圆柱体积相等,所以每一个小圆柱的体积是大圆柱的一半;
切后的小圆柱的侧面积是原圆柱的侧面积的一半,而小圆柱的底面积等于原圆柱的底面积,每个圆柱体的表面积比原圆柱表面积的一半多了一个圆柱的底面积,所以小圆柱的表面积不是原圆柱的表面积的一半;
所以原题说法错误。
故答案为:×。
四.计算题(共2小题)
25.解:3.14×4×1+3.14×(4÷2)2×2
=3.14×4+3.14×4×2
=12.56+25.12
=37.68(平方厘米)
3.14×(4÷2)2×1
=3.14×4×1
=12.56(立方厘米)
答:这个圆柱的表面积是37.68平方厘米,体积是1.56立方厘米。
26.解:3.14×(4÷2)2×2+3.14×4×10
=25.12+125.6
=150.72(平方厘米)
故答案为:150.72。
五.应用题(共6小题)
27.解:3.14×(10÷2)2×150÷5
=3.14×25×150÷5
=11775÷5
=2355(个)
答:这段钢材能生产2355个这种零件。
28.解:圆柱的高:60÷2÷2=15(厘米)
长方体的长:3.14×2=6.28(厘米)
所以长方体的体积:6.28×2×15
=12.56×15
=188.4(立方厘米)
答:这个长方体的体积是188.4立方厘米。
29.解:3×3×6+3.14×2×3﹣3.14×(2÷2)2×2
=54+18.84﹣6.28
=66.56(平方厘米)
答:剩下物体的表面积为66.56平方厘米。
30.解:(850﹣200)﹣(630﹣200)
=650﹣430
=220(立方厘米)
220÷(3﹣1)
=220÷2
=110(立方厘米)
630﹣200﹣110
=430﹣110
=320(立方厘米)
答:大正方体的体积是320立方厘米。
31.解:3.14×(6÷2)2×2.5
=3.14×9×2.5
=70.65(立方米)
答:这个粮囤有小麦70.65立方米。
32.解:[×3.14×(12÷2)2×10]÷[3.14×(15÷2)2]
=[×3.14×36×10]÷56.25
=376.8÷56.25
≈6.7(厘米)
答:把铁块从水中取出,容器中的水面高度将下降6.7厘米。
一.选择题(共7小题)
1.每个面都是正方形的立体图形是( )
A.长方体 B.正方体 C.圆柱
2.将一个圆柱沿底面直径横向切开后,得到的切面是个宽6cm,面积是60cm2的长方形(如图)。原来这个圆柱的体积是( )cm3。
A.188.4 B.282.6 C.360 D.1130.4
3.把一根底面半径是4分米,长是2米的圆柱形钢材截成两根小圆柱形钢材,这两根小圆柱形钢材的表面积之和与原来圆柱形钢材的表面积相比( )。
A.大小不变 B.增加了50.24平方分米
C.增加了100.48平方分米 D.增加了1004.8平方分米
4.将下面一个圆柱体沿着高剪开得到一个长方形,这个长方形的长是( )
A.4厘米 B.7厘米 C.21.98厘米
5.将下面的圆柱体的侧面沿AB展开,所得到的侧面展开图不可能是( )
A.①② B.①③ C.①②③ D.③④
6.如图,把一个长方形分别以长和宽为轴旋转一周形成的圆柱体,体积相比( )
A.长为轴的更大 B.宽为轴的更大
C.相同 D.无法确定
7.下列几何体的展开图中,能围成圆柱的是( )
A. B.
C. D.
二.填空题(共10小题)
8.把1米长的圆柱形木料,沿横截面锯成同样长的3小段,表面积比原来增加了12.56dm2,这根圆柱形木料的体积 dm3。
9.从一个大圆柱体上截下一个高2cm的小圆柱体后,表面积就减少12.56cm2,原来这个圆柱体的底面直径是 cm。
10.做一个底面半径2分米,高5分米的无盖铁皮水桶,至少需要 平方分米的铁皮。(结头处不计)
11.李师傅把一块底面直径是6分米,长15分米的圆柱形木料等分成了3个完全相等的小圆柱。表面积增加了 平方分米,一个小圆柱的体积是 立方分米。
12.一根圆木长6米,如果截去6分米长的一小段圆木后,表面积减少18.84dm2,那么原来这跟原木的体积是 dm3。
13.把一个高为10厘米的圆柱转化成等底等高的长方体。长方体的表面积比圆柱增加了60立方厘米,原来这个圆柱的体积是 立方厘米。
14.把一个棱长为6cm的正方体,削成一个最大的圆柱体,削去部分的体积是 cm3。
15.一个圆柱的底面半径是5厘米,高是10厘米,它的底面积是 平方厘米,侧面积是 平方厘米,体积是 立方厘米。
16.如图,把底面直径为8cm的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的表面积比圆柱多80cm2,那么圆柱的高是 cm,圆柱的体积是 cm3。
17.有一根长2米的圆柱形钢材,如果把它截成5个小圆柱,5个小圆柱的表面积之和比原来增加2512平方厘米。这根圆柱形钢材的体积是 立方厘米。
三.判断题(共7小题)
18.一个圆柱的底面半径是8厘米,它的侧面展开正好是一个正方形,这个圆柱的高是16厘米. .(判断对错)
19.圆柱的底面直径是3厘米,高3π厘米,侧面展开后是一个正方形. .(判断对错)
20.一个圆柱与一个圆锥底面积之比是2:3,高之比是4:5,体积之比是8:15。 (判断对错)
21.三角形绕着一条边旋转后形成的立体图形是圆锥。 (判断对错)
22.把一个圆柱切拼成一个和它体积相等的长方体,推导出圆柱体体积计算公式的这一过程中,运用了转化的数学思想方法。 (判断对错)
23.把一支新的圆柱形铅笔削尖,笔尖(圆锥部分)的体积是削去部分的。 (判断对错)
24.把一个圆柱体平均切成两个小圆柱,每个小圆柱体的体积和表面积都是原来圆柱体的一半。 (判断对错)
四.计算题(共2小题)
25.求如图的表面积和体积。(单位:cm)
26.计算下面圆柱的表面积.
五.应用题(共6小题)
27.一根圆柱形钢材,横截面的直径是10cm,长是150cm。如果加工一个零件需要用去钢材5cm3,这段钢材能生产多少个这种零件?
28.把一个底面半径是2厘米的圆柱体,沿底面直径垂直于高切成若干等份,再拼成一个近似长方体,(如图)已知拼成后长方体表面积比原来圆柱表面积增加了60平方厘米,这个长方体的体积是多少?
29.在一个棱长为3厘米的正方体上面正中央垂直向下挖出一个底面直径是2厘米,高为3厘米的圆柱,剩下物体的表面积为多少?
30.根据下如图玻璃容器中水的变化,你知道大正方体的体积是多少?
31.一个圆柱形粮囤,底面直径6米,装有2.5米高的小麦,这个粮囤有小麦多少立方米?
32.一个圆柱形玻璃容器里装有水,水中浸没着一个底面直径为12cm,高为10cm的圆锥形铁块,如果把它取出那么容器中的水面高度将下降多少厘米?(圆柱形玻璃容器的底面内直径是15厘米)
参考答案
一.选择题(共7小题)
1.解:每个面都是正方形的立体图形是正方体。
故选:B。
2.解:长方形的长:60÷6=10(cm)
圆柱的底面半径:6÷2=3(cm)
圆柱的体积:3.14×3 ×10
=3.14×9×10
=282.6(cm )
答:圆柱的体积是282.6cm 。
故选:B。
3.解:3.14×42×2
=3.14×16×2
=100.48(平方分米)
答:这两根小圆柱形钢材的表面积之和与原来圆柱形钢材的表面积相比增加了100.48平方分米。
故选:C。
4.解:3.14×7=21.98(cm)
答:展开后长方形的长是21.98厘米,C选项正确。
故选:C。
5.解:将圆的侧面沿高展开得到的图形只能为长方形或正方形,不可能是梯形或圆,所以D选项合适。
故选:D。
6.解:以长为轴旋转一周,得到的圆柱的体积:
3.14×42×8
=50.24×8
=401.92(立方厘米)
以宽为轴旋转一周,得到的圆柱的体积:
3.14×82×4
=200.96×4
=803.84(立方厘米)
401.92<803.84,所以以宽为轴旋转一周得到的圆柱体积大.
故选:B。
7.解:选项A,可以围成一个正方体,不符合题意。
选项B,可以围成一个长方体,不符合题意。
选项C,可以围成一个圆柱,符合题意。
选项D,可以围成一个圆锥,不符合题意。
故选:C。
二.填空题(共10小题)
8.解:1米=10分米
12.56÷4×10
=3.14×10
=31.4(dm )
答:这根圆柱形木料的体积31.4dm 。
故答案为:31.4。
9.解:12.56÷2÷3.14
=6.28÷3.14
=2(cm)
答:这个圆柱的底面直径是2cm。
故答案为:2。
10.解:3.14×2 +3.14×2×2×5
=3.14×4+62.8
=12.56+62.8
=75.36(平方分米)
答:至少需要75.36平方分米的铁皮。
故答案为:75.36。
11.解:3.14×(6÷2) ×4
=3.14×9×4
=113.04(平方分米)
3.14×(6÷2) ×15×
=3.14×9×15×
=423.9×
=141.3(立方分米)
答:表面积增加113.04平方分米,一个小圆柱的体积是141.3立方分米。
故答案为:113.04,141.3。
12.解:6米=60分米
18.84÷6=3.14(分米)
3.14÷3.14÷2=0.5(分米)
3.14×0.52×60
=3.14×0.25×60
=0.785×60
=47.1(立方分米)
答:原来这根圆木的体积是47.1立方分米。
故答案为:47.1。
13.解:60÷2÷10
=30÷10
=3(厘米)
3.14×32×10
=3.14×9×10
=28.26×10
=282.6(立方厘米)
答:原来这个圆柱的体积是282.6立方厘米。
故答案为:282.6。
14.解:6×6×6﹣3.14×(6÷2)2×6
=36×6﹣3.14×9×6
=216﹣169.56
=46.44(立方厘米)
答:削去部分的体积是46.44立方厘米。
故答案为:46.44。
15.解:3.14×52
=3.14×25
=78.5(平方厘米)
2×3.14×5×10
=31.4×10
=314(平方厘米)
3.14×52×10
=3.14×25×10
=78.5×10
=785(立方厘米)
答:它的底面积是78.5平方厘米,侧面积是314平方厘米,体积是785立方厘米。
故答案为:78.5、314、785。
16.解:80÷2÷(8÷2)
=40÷4
=10(厘米)
3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方厘米)
答:圆柱的高是10cm,圆柱的体积是502.4cm3。
故答案为:10cm,502.4cm3。
17.解:2米=200厘米
2512÷[(5﹣1)×2]×200
=2512÷[4×2]×200
=2512÷8×200
=314×200
=62800(立方厘米)
答:这根圆柱形钢材的体积是62800立方厘米。
故答案为:62800。
三.判断题(共7小题)
18.解:侧面展开后长方形的长(底面周长)=2πr=2×3.14×8=50.24(厘米);
又因为侧面展开后是正方形,所以:宽=长=50.24厘米;
侧面展开后长方形的宽又是圆柱的高,即高=50.24厘米;
故答案为:×.
19.解:侧面展开后长方形的长(底面周长)=3π厘米,
侧面展开后长方形的宽=圆柱的高=3π厘米,
因为:3π厘米=3π厘米,
所以:侧面展开后长方形的长=宽,此图形是正方形.
故答案为:√
20.解:设圆柱与圆锥的高分别是4h、5h,
圆柱的体积=2×3h=6h,
圆锥的体积=×3×5h=5h,
圆柱和圆锥体积的比是:6h:5h=6:5
答:圆柱和圆锥体积的比是6:5。
因此,题干中的结论是错误的。
故答案为:×。
21.解:如果是直角三角形,旋转一周,可以得到一个圆锥,否则不可能得到一个圆锥。
因此,三角形绕着一条边旋转后形成的立体图形是圆锥。此说法错误。
故答案为:×。
22.解:圆柱体积公式推导过程中,我们把圆柱转化为长方体,也就是把未知方法转化为已知方法,用到的是转化思想;
所以原题说法正确。
故答案为:√。
23.解:1﹣=
÷
=
=
笔尖(圆锥部分)的体积是削去部分的,原题说法正确。
故答案为:√。
24.解:根据分析可得,
把一个圆柱平均切成两个小圆柱,这两个小圆柱等底等高,根据圆柱的体积=底面积×高,可知这两个小圆柱体积相等,所以每一个小圆柱的体积是大圆柱的一半;
切后的小圆柱的侧面积是原圆柱的侧面积的一半,而小圆柱的底面积等于原圆柱的底面积,每个圆柱体的表面积比原圆柱表面积的一半多了一个圆柱的底面积,所以小圆柱的表面积不是原圆柱的表面积的一半;
所以原题说法错误。
故答案为:×。
四.计算题(共2小题)
25.解:3.14×4×1+3.14×(4÷2)2×2
=3.14×4+3.14×4×2
=12.56+25.12
=37.68(平方厘米)
3.14×(4÷2)2×1
=3.14×4×1
=12.56(立方厘米)
答:这个圆柱的表面积是37.68平方厘米,体积是1.56立方厘米。
26.解:3.14×(4÷2)2×2+3.14×4×10
=25.12+125.6
=150.72(平方厘米)
故答案为:150.72。
五.应用题(共6小题)
27.解:3.14×(10÷2)2×150÷5
=3.14×25×150÷5
=11775÷5
=2355(个)
答:这段钢材能生产2355个这种零件。
28.解:圆柱的高:60÷2÷2=15(厘米)
长方体的长:3.14×2=6.28(厘米)
所以长方体的体积:6.28×2×15
=12.56×15
=188.4(立方厘米)
答:这个长方体的体积是188.4立方厘米。
29.解:3×3×6+3.14×2×3﹣3.14×(2÷2)2×2
=54+18.84﹣6.28
=66.56(平方厘米)
答:剩下物体的表面积为66.56平方厘米。
30.解:(850﹣200)﹣(630﹣200)
=650﹣430
=220(立方厘米)
220÷(3﹣1)
=220÷2
=110(立方厘米)
630﹣200﹣110
=430﹣110
=320(立方厘米)
答:大正方体的体积是320立方厘米。
31.解:3.14×(6÷2)2×2.5
=3.14×9×2.5
=70.65(立方米)
答:这个粮囤有小麦70.65立方米。
32.解:[×3.14×(12÷2)2×10]÷[3.14×(15÷2)2]
=[×3.14×36×10]÷56.25
=376.8÷56.25
≈6.7(厘米)
答:把铁块从水中取出,容器中的水面高度将下降6.7厘米。
