人教版 五年级数学下册第4单元 真分数和假分数 教案
文档属性
| 名称 | 人教版 五年级数学下册第4单元 真分数和假分数 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 227.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 17:22:34 | ||
图片预览




文档简介
2 真分数和假分数
本小节对分数进行分类,根据分数与1的大小比较可知分数可以分为真分数和假分数(带分数是假分数的另一种书写形式)。通过学习真分数、假分数以及带分数,可以使学生比较全面地理解分数概念,也有利于培养学生关于分数的数感。
例1认识真分数。教材借助涂色帮助学生直观地理解真分数的概念。例2先认识假分数,接着引出带分数的概念。并明确指出:假分数的分子是分母的倍数的,是整数;假分数的分子不是分母的倍数的,是带分数。为后面学习假分数的转化做准备。例3教学假分数化成整数或带分数。
1.使学生理解真分数、假分数和带分数的意义。使学生知道真分数小于1,假分数大于或等于1这些特征。能把假分数化成带分数或整数。
2.培养学生观察比较、抽象概括的能力。
3.体验探究的乐趣,渗透转化的数学思想。
【重点】 理解真分数、假分数的概念和特征。
【难点】 认识假分数,知道分子等于分母的分数也是假分数。
【教师准备】 PPT课件。
【学生准备】 正方形或圆形纸片。
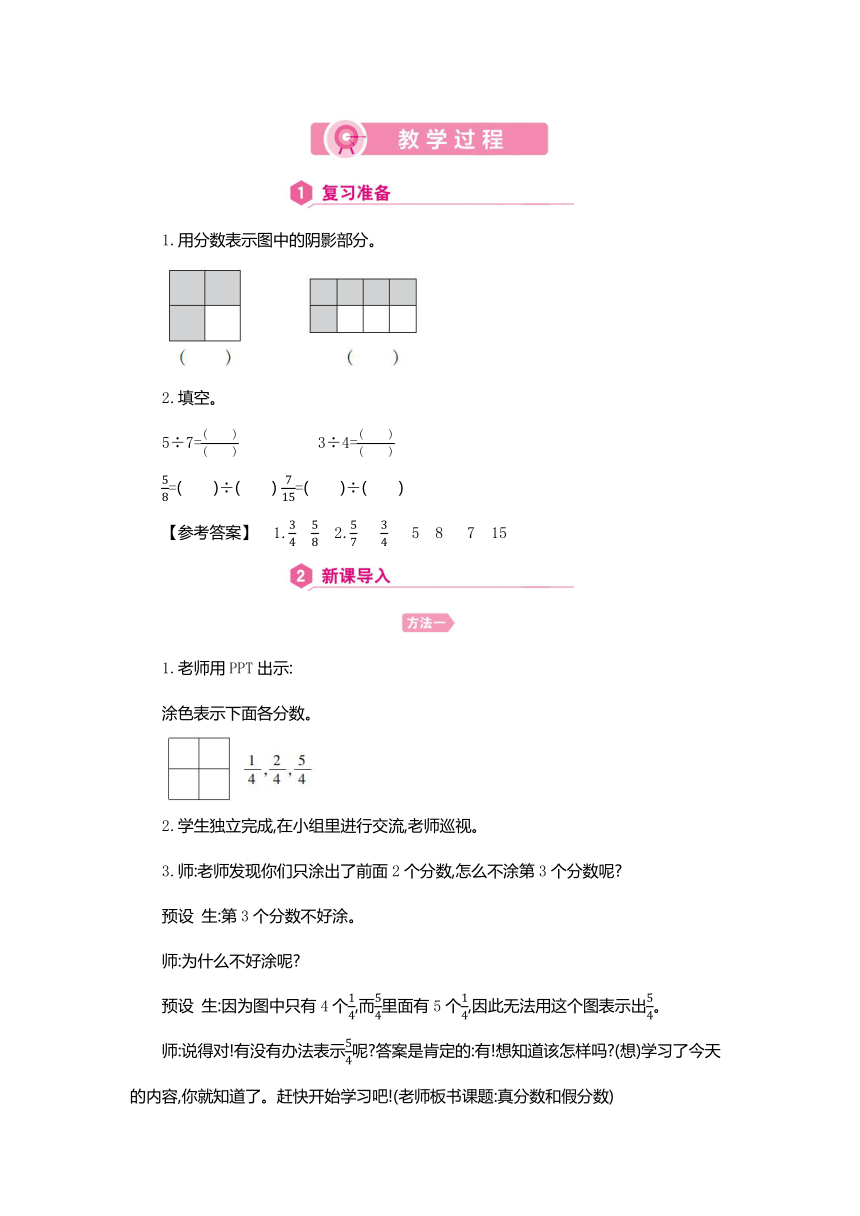
1.用分数表示图中的阴影部分。
2.填空。
5÷7= 3÷4=
=( )÷( ) =( )÷( )
【参考答案】 1. 2. 5 8 7 15
1.老师用PPT出示:
涂色表示下面各分数。
2.学生独立完成,在小组里进行交流,老师巡视。
3.师:老师发现你们只涂出了前面2个分数,怎么不涂第3个分数呢
预设 生:第3个分数不好涂。
师:为什么不好涂呢
预设 生:因为图中只有4个,而里面有5个,因此无法用这个图表示出。
师:说得对!有没有办法表示呢 答案是肯定的:有!想知道该怎样吗 (想)学习了今天的内容,你就知道了。赶快开始学习吧!(老师板书课题:真分数和假分数)
在解决问题的过程中遇到了无法解决的问题,促使学生有了学习新知的欲望。激发了学生的学习兴趣。
1.老师用PPT出示一组分数,让学生把这些分数分成两类。
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
(1)学生独立完成,老师巡视了解学情。
(2)指名回答。
预设 生:我是这样分的:第一类是①③④⑤⑧⑩这6个分数,
第二类是②⑥⑦⑨这4个分数。
老师根据学生的回答板书。
师:你是根据什么进行分类的
预设 生:我是比较了它们的分子和分母的大小后进行分类的,第一类的分子都比分母小;第二类的分子都比分母大。
师:这位同学分的是正确的,你们也是这样分的吗
……
2.揭示课题:(老师指着分数说)这两类分数都有各自的名字,(老师板书:真分数和假分数)它们也有不同的特征,今天我们就一起来探究这些分数的特征。
运用学生已有的分类的知识,对一些分数进行分类,培养和锻炼学生的观察、分析能力,并通过分类的结果导入新知的学习。
一、教学例1,使学生认识真分数,知道真分数小于1。
1.老师用PPT出示例1。
(1)学生读题,引导学生涂色表示题中各分数,并让学生说说把什么作为单位“1”。
预设 生:图一是把一个圆看作单位“1”,平均分成3份,我涂了1份,表示;图二是把一个圆看作单位“1” ,平均分成4份,我涂了3份,表示;图三还是把一个圆看作单位“1”,平均分成6份,我涂了5份,表示。
老师根据学生的回答,将PPT中的图涂色。
(2)用PPT出示小精灵说的一段话,引导学生读一读并回答。
预设 生:的分数单位是,它有1个这样的分数单位。的分数单位是,它有3个这样的分数单位。的分数单位是,它有5个这样的分数单位。
(3)引导学生比较例1中三个分数的分子和分母的大小。你发现了什么
预设 生:这几个分数的分子都比分母小。
(4)引导学生观察例1中的几个图,想一想:这些分数比1大,还是比1小 为什么
预设 生:,,这几个分数都比1小,因为它们都是从单位“1”里取出其中的几份。
2.老师引导学生归纳小结:像这样,分子比分母小的分数叫做真分数,真分数小于1。(老师板书)
二、教学例2,使学生认识假分数,知道假分数大于或等于1;认识带分数,知道带分数是由整数和真分数合成的数。明确有些假分数的分子恰好是分母的倍数,它们实际上是整数,有些假分数的分子不是分母的倍数,这样的假分数可以写成带分数。
1.老师用PPT出示例2。
(1)学生读题,理解把一个圆作为单位“1”,然后独立完成第(1)题。
(2)老师巡视指导,指名回答。
预设 生:4个是,涂满一个圆是3个,还剩,要在第二个圆里再涂1份,也就是1个。
根据学生的回答,老师用PPT将第(1)题中圆涂色。
(3)学生根据第(2)题的要求涂色,老师巡视指导,选择学生作业进行展示。
(4)引导学生观察例2中的分数,想一想:这些分数比1大,还是比1小
预设 生:从图中可以看出,和都比1大,而等于1。
老师根据学生回答板书:大于1或等于1。
(5)像,,和这样的分数叫做假分数,谁能说说什么样的分数叫假分数
预设 生:分子比分母大或分子与分母相等的分数,叫做假分数。
2.老师引导学生归纳小结:像这样,分子比分母大或分子和分母相等的分数叫做假分数,假分数大于1或等于1。(老师板书)
3.引导学生观察第(2)题中的图三,认识带分数。
(1)观察涂色结果,你发现了什么
预设 生:在涂色时涂了2个圆和1个圆的。
(2)老师揭示带分数的概念以及读写法。
从涂色的结果可以看出,可以看作是由2和合成的数,可以写作2,读作:二又五分之一。像这样由整数和真分数合成的数叫做带分数。
(3)学生在小组里读一读。
1,6,5,7
三、教学例3,使学生掌握把假分数化成整数或带分数的方法。
师:有时根据需要,要把假分数化成整数或带分数。
1.用PPT出示例3(1)。
(1)学生分小组进行讨论,老师巡视了解学情,适时进行指导。
(2)指名回答,重点说出自己是怎样把化成整数的。
预设 生1:根据分数的意义可知3个就是1,所以=1。
生2:根据分数与除法的关系,用3÷3=1,所以=3÷3=1。
生3:看图可知正好涂满了一个圆,所以=1。
(3)学生在小组里按照上面的方法互相说一说怎样把化成整数。
(4)小结:当分数的分子正好是分母的倍数时,这个假分数实际上是整数,把假分数化成整数用分子除以分母。(板书)
2.用PPT出示例3(2)。
(1)学生分小组进行讨论,老师巡视了解学情,适时进行指导。
(2)学生写出结果,然后在小组内进行交流,再指名回答。
预设 生1:是(就是2)和合成的数,=2。
生2:=7÷3=2。
生3:=6÷5=1。
(3)小结:当假分数的分子不是分母的倍数时,这样的假分数可以化成带分数。把假分数化成带分数,用分子除以分母,商是带分数的整数部分,余数是分子,分母不变。(板书)
3.巩固练习。
(1)读出下面各分数。
3,4,2,8。
(2)把下面分数化成整数或带分数。
,,,。
【参考答案】 (1)三又五分之一,四又四分之三,二又三分之一,八又六分之五。
(2)=2,=3,=1,=3。
练习1
1.教材第54页“做一做”。
2.教材第55页练习十三第1,2题。
3.教材第56页练习十三第9题。
练习2
完成相关习题。
师:通过这节课的学习你知道了哪些新知识
预设 生:我认识了真分数,知道真分数小于1;认识了假分数,知道假分数大于1或等于1;认识了带分数,知道带分数是由整数和真分数合成的数。还学会了把假分数化成整数或带分数。
作业1
1.教材第55页练习十三第3,4题。
2.教材第56页练习十三第6,7题。
作业2
完成相关习题。
真分数和假分数 例1:,,。
分子比分母小的分数叫做真分数。
真分数小于1。
例2:(1) (2)
分子比分母大或分子和分母相等的分
数叫做假分数。假分数大于1或等于1。
2读作:二又五分之一
由整数和真分数合成的数叫做带分数。 例3:(1)=3÷3=1
=8÷4=2
(2)=7÷3=2
=6÷5=1
本节课的教学虽然学习的内容比较多,但是学生掌握的情况还是比较好。因为在教学中,注意让学生根据课本自学,在小组里讨论、交流,因此课堂氛围活跃,学生学习积极性高。教学中的重点、难点在学生的讨论、交流中得到了解决。我觉得这节课最成功的就是组织好了小组的合作学习。
有的学生在回答问题不准确时,没有让学生多交流,而是老师直接指出错误。
再教时,遇到类似情况,可以让学生进行充分的讨论。学生与学生的交流更能引起共鸣。
把下面的分数在下图中表示出来。
[名师点拨] 首先看所要表示的分数是多少,小于1的分数,分母是几,就把0到1之间的线段平均分成几份,分子是几就选几份标出对应点。如果分数大于1而小于2,也是看分母是几,把0到1和1到2之间的线段都平均分成几份,然后标出分子所表示的份数的点。
[解答] 如下图所示。
【知识拓展】 带分数也可以用直线上的点表示,带分数的整数部分是几,所要表示的点就在这个数和比它大1的自然数之间,然后看分母是几,再把这两个数之间的线段平均分成几份,标出分子所表示的份数的点即可。
真分数与假分数
在人类历史上,最初产生的分数是作为整体或一个单位的一部分,这样的分数叫做真分数。后来,为了满足数系扩充的需要,把整数看成分母是1的分数,这样的分数就是假分数。
关于分数的拓展
小学数学中对分数的定义是:把单位“1”平均分成若干份,表示这样的一份或几份的数叫分数。因此分数的分子、分母都是非0自然数,并且分母不能是1。
在过去的小学数学课本中,有繁分数的概念。如:,都可以看成繁分数。繁分数可以化成整数或分数。
在计算中,有时会出现分子是0的分数,就叫零分数;分母是1的分数,实际上就是整数。所以分数的补充定义是:分数,当n=1时,==m;分数,当m=0时,==0。
本小节对分数进行分类,根据分数与1的大小比较可知分数可以分为真分数和假分数(带分数是假分数的另一种书写形式)。通过学习真分数、假分数以及带分数,可以使学生比较全面地理解分数概念,也有利于培养学生关于分数的数感。
例1认识真分数。教材借助涂色帮助学生直观地理解真分数的概念。例2先认识假分数,接着引出带分数的概念。并明确指出:假分数的分子是分母的倍数的,是整数;假分数的分子不是分母的倍数的,是带分数。为后面学习假分数的转化做准备。例3教学假分数化成整数或带分数。
1.使学生理解真分数、假分数和带分数的意义。使学生知道真分数小于1,假分数大于或等于1这些特征。能把假分数化成带分数或整数。
2.培养学生观察比较、抽象概括的能力。
3.体验探究的乐趣,渗透转化的数学思想。
【重点】 理解真分数、假分数的概念和特征。
【难点】 认识假分数,知道分子等于分母的分数也是假分数。
【教师准备】 PPT课件。
【学生准备】 正方形或圆形纸片。
1.用分数表示图中的阴影部分。
2.填空。
5÷7= 3÷4=
=( )÷( ) =( )÷( )
【参考答案】 1. 2. 5 8 7 15
1.老师用PPT出示:
涂色表示下面各分数。
2.学生独立完成,在小组里进行交流,老师巡视。
3.师:老师发现你们只涂出了前面2个分数,怎么不涂第3个分数呢
预设 生:第3个分数不好涂。
师:为什么不好涂呢
预设 生:因为图中只有4个,而里面有5个,因此无法用这个图表示出。
师:说得对!有没有办法表示呢 答案是肯定的:有!想知道该怎样吗 (想)学习了今天的内容,你就知道了。赶快开始学习吧!(老师板书课题:真分数和假分数)
在解决问题的过程中遇到了无法解决的问题,促使学生有了学习新知的欲望。激发了学生的学习兴趣。
1.老师用PPT出示一组分数,让学生把这些分数分成两类。
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
(1)学生独立完成,老师巡视了解学情。
(2)指名回答。
预设 生:我是这样分的:第一类是①③④⑤⑧⑩这6个分数,
第二类是②⑥⑦⑨这4个分数。
老师根据学生的回答板书。
师:你是根据什么进行分类的
预设 生:我是比较了它们的分子和分母的大小后进行分类的,第一类的分子都比分母小;第二类的分子都比分母大。
师:这位同学分的是正确的,你们也是这样分的吗
……
2.揭示课题:(老师指着分数说)这两类分数都有各自的名字,(老师板书:真分数和假分数)它们也有不同的特征,今天我们就一起来探究这些分数的特征。
运用学生已有的分类的知识,对一些分数进行分类,培养和锻炼学生的观察、分析能力,并通过分类的结果导入新知的学习。
一、教学例1,使学生认识真分数,知道真分数小于1。
1.老师用PPT出示例1。
(1)学生读题,引导学生涂色表示题中各分数,并让学生说说把什么作为单位“1”。
预设 生:图一是把一个圆看作单位“1”,平均分成3份,我涂了1份,表示;图二是把一个圆看作单位“1” ,平均分成4份,我涂了3份,表示;图三还是把一个圆看作单位“1”,平均分成6份,我涂了5份,表示。
老师根据学生的回答,将PPT中的图涂色。
(2)用PPT出示小精灵说的一段话,引导学生读一读并回答。
预设 生:的分数单位是,它有1个这样的分数单位。的分数单位是,它有3个这样的分数单位。的分数单位是,它有5个这样的分数单位。
(3)引导学生比较例1中三个分数的分子和分母的大小。你发现了什么
预设 生:这几个分数的分子都比分母小。
(4)引导学生观察例1中的几个图,想一想:这些分数比1大,还是比1小 为什么
预设 生:,,这几个分数都比1小,因为它们都是从单位“1”里取出其中的几份。
2.老师引导学生归纳小结:像这样,分子比分母小的分数叫做真分数,真分数小于1。(老师板书)
二、教学例2,使学生认识假分数,知道假分数大于或等于1;认识带分数,知道带分数是由整数和真分数合成的数。明确有些假分数的分子恰好是分母的倍数,它们实际上是整数,有些假分数的分子不是分母的倍数,这样的假分数可以写成带分数。
1.老师用PPT出示例2。
(1)学生读题,理解把一个圆作为单位“1”,然后独立完成第(1)题。
(2)老师巡视指导,指名回答。
预设 生:4个是,涂满一个圆是3个,还剩,要在第二个圆里再涂1份,也就是1个。
根据学生的回答,老师用PPT将第(1)题中圆涂色。
(3)学生根据第(2)题的要求涂色,老师巡视指导,选择学生作业进行展示。
(4)引导学生观察例2中的分数,想一想:这些分数比1大,还是比1小
预设 生:从图中可以看出,和都比1大,而等于1。
老师根据学生回答板书:大于1或等于1。
(5)像,,和这样的分数叫做假分数,谁能说说什么样的分数叫假分数
预设 生:分子比分母大或分子与分母相等的分数,叫做假分数。
2.老师引导学生归纳小结:像这样,分子比分母大或分子和分母相等的分数叫做假分数,假分数大于1或等于1。(老师板书)
3.引导学生观察第(2)题中的图三,认识带分数。
(1)观察涂色结果,你发现了什么
预设 生:在涂色时涂了2个圆和1个圆的。
(2)老师揭示带分数的概念以及读写法。
从涂色的结果可以看出,可以看作是由2和合成的数,可以写作2,读作:二又五分之一。像这样由整数和真分数合成的数叫做带分数。
(3)学生在小组里读一读。
1,6,5,7
三、教学例3,使学生掌握把假分数化成整数或带分数的方法。
师:有时根据需要,要把假分数化成整数或带分数。
1.用PPT出示例3(1)。
(1)学生分小组进行讨论,老师巡视了解学情,适时进行指导。
(2)指名回答,重点说出自己是怎样把化成整数的。
预设 生1:根据分数的意义可知3个就是1,所以=1。
生2:根据分数与除法的关系,用3÷3=1,所以=3÷3=1。
生3:看图可知正好涂满了一个圆,所以=1。
(3)学生在小组里按照上面的方法互相说一说怎样把化成整数。
(4)小结:当分数的分子正好是分母的倍数时,这个假分数实际上是整数,把假分数化成整数用分子除以分母。(板书)
2.用PPT出示例3(2)。
(1)学生分小组进行讨论,老师巡视了解学情,适时进行指导。
(2)学生写出结果,然后在小组内进行交流,再指名回答。
预设 生1:是(就是2)和合成的数,=2。
生2:=7÷3=2。
生3:=6÷5=1。
(3)小结:当假分数的分子不是分母的倍数时,这样的假分数可以化成带分数。把假分数化成带分数,用分子除以分母,商是带分数的整数部分,余数是分子,分母不变。(板书)
3.巩固练习。
(1)读出下面各分数。
3,4,2,8。
(2)把下面分数化成整数或带分数。
,,,。
【参考答案】 (1)三又五分之一,四又四分之三,二又三分之一,八又六分之五。
(2)=2,=3,=1,=3。
练习1
1.教材第54页“做一做”。
2.教材第55页练习十三第1,2题。
3.教材第56页练习十三第9题。
练习2
完成相关习题。
师:通过这节课的学习你知道了哪些新知识
预设 生:我认识了真分数,知道真分数小于1;认识了假分数,知道假分数大于1或等于1;认识了带分数,知道带分数是由整数和真分数合成的数。还学会了把假分数化成整数或带分数。
作业1
1.教材第55页练习十三第3,4题。
2.教材第56页练习十三第6,7题。
作业2
完成相关习题。
真分数和假分数 例1:,,。
分子比分母小的分数叫做真分数。
真分数小于1。
例2:(1) (2)
分子比分母大或分子和分母相等的分
数叫做假分数。假分数大于1或等于1。
2读作:二又五分之一
由整数和真分数合成的数叫做带分数。 例3:(1)=3÷3=1
=8÷4=2
(2)=7÷3=2
=6÷5=1
本节课的教学虽然学习的内容比较多,但是学生掌握的情况还是比较好。因为在教学中,注意让学生根据课本自学,在小组里讨论、交流,因此课堂氛围活跃,学生学习积极性高。教学中的重点、难点在学生的讨论、交流中得到了解决。我觉得这节课最成功的就是组织好了小组的合作学习。
有的学生在回答问题不准确时,没有让学生多交流,而是老师直接指出错误。
再教时,遇到类似情况,可以让学生进行充分的讨论。学生与学生的交流更能引起共鸣。
把下面的分数在下图中表示出来。
[名师点拨] 首先看所要表示的分数是多少,小于1的分数,分母是几,就把0到1之间的线段平均分成几份,分子是几就选几份标出对应点。如果分数大于1而小于2,也是看分母是几,把0到1和1到2之间的线段都平均分成几份,然后标出分子所表示的份数的点。
[解答] 如下图所示。
【知识拓展】 带分数也可以用直线上的点表示,带分数的整数部分是几,所要表示的点就在这个数和比它大1的自然数之间,然后看分母是几,再把这两个数之间的线段平均分成几份,标出分子所表示的份数的点即可。
真分数与假分数
在人类历史上,最初产生的分数是作为整体或一个单位的一部分,这样的分数叫做真分数。后来,为了满足数系扩充的需要,把整数看成分母是1的分数,这样的分数就是假分数。
关于分数的拓展
小学数学中对分数的定义是:把单位“1”平均分成若干份,表示这样的一份或几份的数叫分数。因此分数的分子、分母都是非0自然数,并且分母不能是1。
在过去的小学数学课本中,有繁分数的概念。如:,都可以看成繁分数。繁分数可以化成整数或分数。
在计算中,有时会出现分子是0的分数,就叫零分数;分母是1的分数,实际上就是整数。所以分数的补充定义是:分数,当n=1时,==m;分数,当m=0时,==0。
