广东省梅州市某重点中学2012-2013学年高二上学期期中数学文试题
文档属性
| 名称 | 广东省梅州市某重点中学2012-2013学年高二上学期期中数学文试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 245.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-04 00:00:00 | ||
图片预览


文档简介
2012年下期高二级期中考试
文科数学
一、选择题(本大题共8小题,每小题5分,共40分) 1.下列条件中,能判断两个平面平行的是
A.一个平面内的一条直线平行于另一个平面;
B.一个平面内的两条直线平行于另一个平面
C.一个平面内有无数条直线平行于另一个平面
D.一个平面内任何一条直线都平行于另一个平面
2..平面α上有不共线三点到平面β的距离相等,则α与β的位置关系为
(A)平行 (B)相交 (C)平行或相交 (D)垂直
3..给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直; ③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是
A.①和② B.②和③ C.③和④ D.②和④
4.棱长都是1的三棱锥的表面积为( ) A. B. C. D. 5.利用斜二测画法得到的 [来源:21世纪教育网]
①三角形的直观图一定是三角形;
②正方形的直观图一定是菱形;
③等腰梯形的直观图可以是平行四边形;
④菱形的直观图一定是菱形.
以上结论正确的是
A.①② B. ① C.③④ D. ①②③④
6.三棱锥P—ABC中,若PA⊥平面ABC,∠ACB=90°,那么在三棱锥的侧面和底面中,直角三角形的个数为
A.4个 B. 3个 C. 2个 D. 1个
7.一个球的外切正方体的全面积等于6 cm2,则此球的体积为 A. B. C. D.
8.如右图为一个几何体的三视图,其中府视图为正三角形,A1B1=2,AA1=4,则该几何体的表面积为21世纪教育网 A. B. C. D.32 9.若l、m、n是互不相同的空间直线,,是不重合的平面,则下列命题中为真命题的是
A.若,则 B.若,则 C. 若,则 D.若,则⊥
10.在平面内有≥条直线,其中任何两条不平行,任何三条不过同一点,若这条直线把平面分成个平面区域,则等于( )A.18 B.22 C.24 D.32
二、填空题(本大题共4小题,每小题5分,共20分
11.E,F, G分别是四面体ABCD的棱BC,CD,DA的中点,则此四面体中与过E,F,G的截面平行的棱的条数是 条
12.圆柱的侧面展开图是边长为4的正方形,则圆柱的体积是
13. 如下图则该几何体的侧面积为 21世纪教育网[来源:21世纪教育网]
14. 已知是两个不同的平面,m、n是平面之外的两条不同的直线,给出四个论断:
①m⊥n,②,③,④。
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题______________。
[来源:21世纪教育网]
三.解答题(本大题共6小题,共80分)
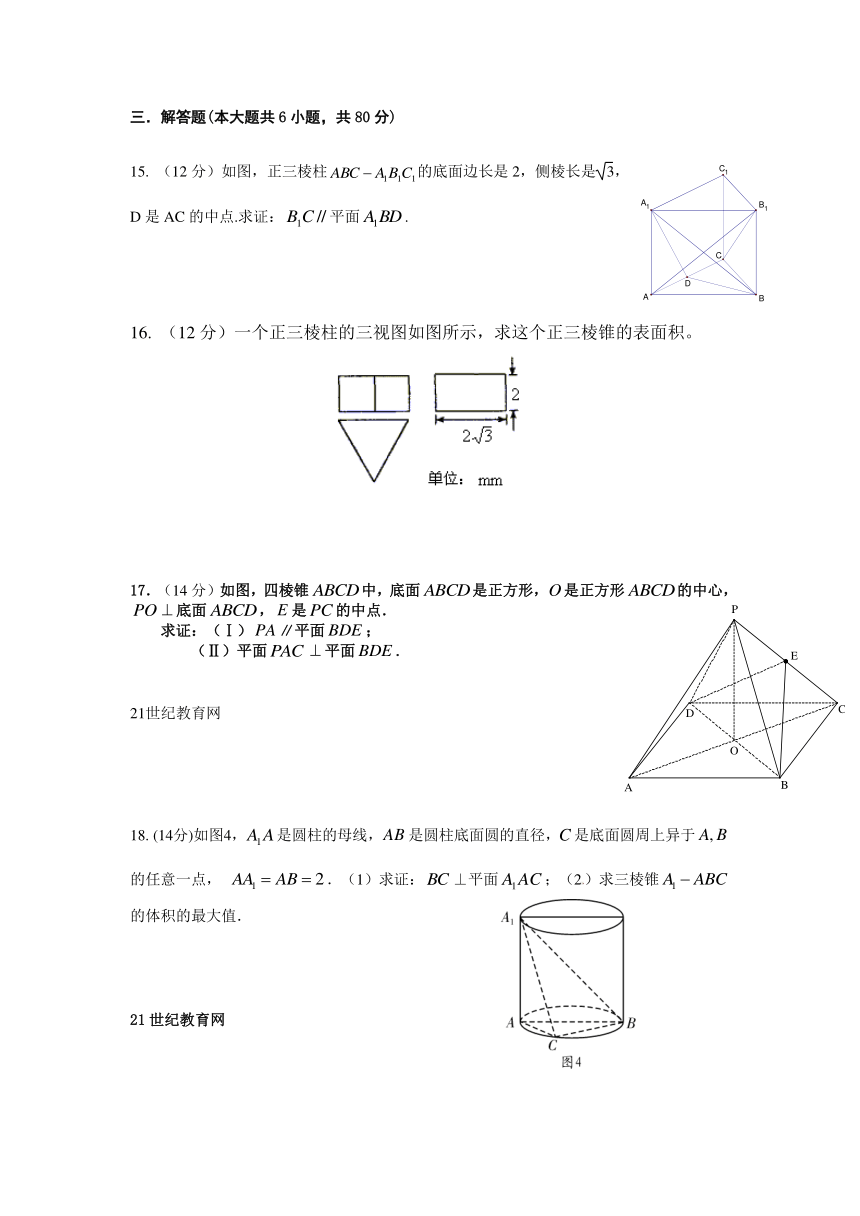
15. (12分)如图,正三棱柱的底面边长是2,侧棱长是,D是AC的中点.求证:平面.
16. (12分)一个正三棱柱的三视图如图所示,求这个正三棱锥的表面积。
17.(14分)如图,四棱锥中,底面是正方形,是正方形的中心,底面,是的中点.
求证:(Ⅰ)∥平面;
(Ⅱ)平面平面.
21世纪教育网
18. (14分)如图4,是圆柱的母线,是圆柱底面圆的直径,是底面圆周上异于的任意一点, .(1)求证:⊥平面;(2)求三棱锥的体积的最大值.
21世纪教育网
19.(14分)一个几何体是由圆柱和三棱锥组合而成,点、、在圆的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图2所示,其中,,,. (1)求证:;(2)求三棱锥的体积.
21世纪教育网
21世纪教育网
20. (14分)如图,正四棱柱中,底面边长为,侧棱长为4,E、F分别为AB、BC的中点,。
(1)求证:平面;
(2)求点到平面的距离d;
(3)求三棱锥的体积V。
21世纪教育网
文科数学参考答案
一、选择题。
1-4DCDA, 5-8BACC, 9-10DB
二、填空题.
11.2 12. 13.80 14.
三.解答题
15.证明:设与相交于点P,连接PD,则P为中点,
D为AC中点,PD//.
又PD平面D,//平面D 21世纪教育网21世纪教育网
16.解:由三视图知正三棱锥的高为2mm
由左视图知正三棱锥的底面三角形的高为
设底面边长为a,则
∴正三棱柱的表面积
17.证明:(Ⅰ)连结.
∵是的中点, 是的中点,21世纪教育网
∴∥,
又∵平面,平面,
∴∥平面.
(Ⅱ)∵底面,
∴,
又∵,且=,
∴平面.
而平面,
∴平面平面.
18.(1)证明:∵是圆周上异于、的一点,且为直径,∴. ∵⊥面,面,∴.∵面,面,∴面.21世纪教育网
(2)解法1:设,在Rt△ 中,(0<x<2,
故(0<x<2,
即.
∵,∴当,即时,三棱锥的体积的最大值为.
19.(1)证明:因为,,所以,即.
又因为,,所以面.因为,所以.
(2)解:因为点、、在圆的圆周上,且,所以为圆的直径.21世纪教育网
设圆的半径为,圆柱高为,根据正(主)视图、侧(左)视图的面积可得,
解得 所以,.
由(1)知,面,所以. 因为,,
所以,即.其中,因为,,21世纪教育网
所以. 所以.
20.(1)如图,连结AC
∵正四棱柱的底面呈正方形
∴AC⊥BD
又AC⊥
∴AC⊥平面
∵E、F分别为AB、BC的中点
∴EF//AC
∴EF⊥平面
∴平面
解(2)在对角面中,作,垂足为H
∵平面,且平面平面
∴21世纪教育网
∴为点到平面的距离
在Rt△中,
(2)
21世纪教育网
文科数学
一、选择题(本大题共8小题,每小题5分,共40分) 1.下列条件中,能判断两个平面平行的是
A.一个平面内的一条直线平行于另一个平面;
B.一个平面内的两条直线平行于另一个平面
C.一个平面内有无数条直线平行于另一个平面
D.一个平面内任何一条直线都平行于另一个平面
2..平面α上有不共线三点到平面β的距离相等,则α与β的位置关系为
(A)平行 (B)相交 (C)平行或相交 (D)垂直
3..给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直; ③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是
A.①和② B.②和③ C.③和④ D.②和④
4.棱长都是1的三棱锥的表面积为( ) A. B. C. D. 5.利用斜二测画法得到的 [来源:21世纪教育网]
①三角形的直观图一定是三角形;
②正方形的直观图一定是菱形;
③等腰梯形的直观图可以是平行四边形;
④菱形的直观图一定是菱形.
以上结论正确的是
A.①② B. ① C.③④ D. ①②③④
6.三棱锥P—ABC中,若PA⊥平面ABC,∠ACB=90°,那么在三棱锥的侧面和底面中,直角三角形的个数为
A.4个 B. 3个 C. 2个 D. 1个
7.一个球的外切正方体的全面积等于6 cm2,则此球的体积为 A. B. C. D.
8.如右图为一个几何体的三视图,其中府视图为正三角形,A1B1=2,AA1=4,则该几何体的表面积为21世纪教育网 A. B. C. D.32 9.若l、m、n是互不相同的空间直线,,是不重合的平面,则下列命题中为真命题的是
A.若,则 B.若,则 C. 若,则 D.若,则⊥
10.在平面内有≥条直线,其中任何两条不平行,任何三条不过同一点,若这条直线把平面分成个平面区域,则等于( )A.18 B.22 C.24 D.32
二、填空题(本大题共4小题,每小题5分,共20分
11.E,F, G分别是四面体ABCD的棱BC,CD,DA的中点,则此四面体中与过E,F,G的截面平行的棱的条数是 条
12.圆柱的侧面展开图是边长为4的正方形,则圆柱的体积是
13. 如下图则该几何体的侧面积为 21世纪教育网[来源:21世纪教育网]
14. 已知是两个不同的平面,m、n是平面之外的两条不同的直线,给出四个论断:
①m⊥n,②,③,④。
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题______________。
[来源:21世纪教育网]
三.解答题(本大题共6小题,共80分)
15. (12分)如图,正三棱柱的底面边长是2,侧棱长是,D是AC的中点.求证:平面.
16. (12分)一个正三棱柱的三视图如图所示,求这个正三棱锥的表面积。
17.(14分)如图,四棱锥中,底面是正方形,是正方形的中心,底面,是的中点.
求证:(Ⅰ)∥平面;
(Ⅱ)平面平面.
21世纪教育网
18. (14分)如图4,是圆柱的母线,是圆柱底面圆的直径,是底面圆周上异于的任意一点, .(1)求证:⊥平面;(2)求三棱锥的体积的最大值.
21世纪教育网
19.(14分)一个几何体是由圆柱和三棱锥组合而成,点、、在圆的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图2所示,其中,,,. (1)求证:;(2)求三棱锥的体积.
21世纪教育网
21世纪教育网
20. (14分)如图,正四棱柱中,底面边长为,侧棱长为4,E、F分别为AB、BC的中点,。
(1)求证:平面;
(2)求点到平面的距离d;
(3)求三棱锥的体积V。
21世纪教育网
文科数学参考答案
一、选择题。
1-4DCDA, 5-8BACC, 9-10DB
二、填空题.
11.2 12. 13.80 14.
三.解答题
15.证明:设与相交于点P,连接PD,则P为中点,
D为AC中点,PD//.
又PD平面D,//平面D 21世纪教育网21世纪教育网
16.解:由三视图知正三棱锥的高为2mm
由左视图知正三棱锥的底面三角形的高为
设底面边长为a,则
∴正三棱柱的表面积
17.证明:(Ⅰ)连结.
∵是的中点, 是的中点,21世纪教育网
∴∥,
又∵平面,平面,
∴∥平面.
(Ⅱ)∵底面,
∴,
又∵,且=,
∴平面.
而平面,
∴平面平面.
18.(1)证明:∵是圆周上异于、的一点,且为直径,∴. ∵⊥面,面,∴.∵面,面,∴面.21世纪教育网
(2)解法1:设,在Rt△ 中,(0<x<2,
故(0<x<2,
即.
∵,∴当,即时,三棱锥的体积的最大值为.
19.(1)证明:因为,,所以,即.
又因为,,所以面.因为,所以.
(2)解:因为点、、在圆的圆周上,且,所以为圆的直径.21世纪教育网
设圆的半径为,圆柱高为,根据正(主)视图、侧(左)视图的面积可得,
解得 所以,.
由(1)知,面,所以. 因为,,
所以,即.其中,因为,,21世纪教育网
所以. 所以.
20.(1)如图,连结AC
∵正四棱柱的底面呈正方形
∴AC⊥BD
又AC⊥
∴AC⊥平面
∵E、F分别为AB、BC的中点
∴EF//AC
∴EF⊥平面
∴平面
解(2)在对角面中,作,垂足为H
∵平面,且平面平面
∴21世纪教育网
∴为点到平面的距离
在Rt△中,
(2)
21世纪教育网
同课章节目录
